[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Ricreazioni di Maggio 2002
![]()
230. Un problema di Dudeney
di Ivana
1) Smith, Jones e Robinson sono il frenatore,
il fuochista e l'ingegnere di un treno, ma non sono
elencati esattamente in questo ordine. Sul treno vi sono tre
passeggeri con gli stessi tre nomi, identificati nelle
premesse seguenti mediante un "Sig." anteposto ai
nomi.
2) Il Sig.Robinson vive a Los Angeles.
3) Il frenatore vive ad Omaha
4) Il Sig. Jones ha da parecchio tempo dimenticato tutta l'algebra
imparata nelle scuole superiori.
5) Il passeggero che ha lo stesso nome del frenatore vive a
Chicago.
6) Il frenatore ed uno dei passeggeri, un eminente fisico
matematico, frequentano la stessa chiesa.
7) Smith batte il fuochista al biliardo.
Chi è l'ingegnere?
>>> Risposte & riflessioni
Dino e Ivana Niccolai
L'ingegnere del treno è Smith.
Infatti, per la premessa (7) si elimina la possibilità che Smith sia il fuochista; per la premessa (2) invece si sa che il Sig. Robinson vive a Los Angeles, e dato che ogni passeggero proviene da un posto differente sia il Sig. Smith che il Sig. Jones sicuramente non vivono a Los Angeles. Secondo questi dati possiamo riportare pertanto due tabelle riepilogative parziali:
Nome |
Frenatore |
Fuochista |
Ingegnere |
Smith |
NO |
||
Jones |
|||
Robinson |
Nome |
Los Angeles |
Omaha |
Chicago |
Sig. Smith |
NO |
||
Sig. Jones |
NO |
||
Sig. Robinson |
SI |
NO |
NO |
I dati del problema, nelle affermazioni (3) e (6), ci dicono che il fisico vive a Omaha; egli non può logicamente essere il Sig. Robinson, che abita a Los Angeles, e neppure il Sig. Jones il quale ha dimenticato l'algebra, quindi deve essere necessariamente il Sig. Smith. Di conseguenza il Sig. Jones non abita a Omaha e, per esclusione, vive a Chicago. La tabella relativa ai passeggeri è quindi così completata:
Nome |
Los Angeles |
Omaha |
Chicago |
Sig. Smith |
NO |
SI |
NO |
Sig. Jones |
NO |
NO |
SI |
Sig. Robinson |
SI |
NO |
NO |
Per completare anche quella relativa alle professioni esaminiamo la premessa (5) del problema: possiamo adesso capire che il frenatore si chiama Jones. Le ultime deduzioni sono semplici: il fuochista non potendo essere né Jones e né, per la premessa (7), Smith, sarà ovviamente Robinson e per esclusione Smith è, quindi, l'ingegnere! Dunque anche la prima tabella è completa:
Nome |
Frenatore |
Fuochista |
Ingegnere |
Smith |
NO |
NO |
SI |
Jones |
SI |
NO |
NO |
Robinson |
NO |
SI |
NO |
Riccardo Fusilli giunge alla stessa conclusione ma presenta il suo ragionamento in un modo diverso.
Ho provato a risolvere la ricreazione n.230
di Ivana ed ho seguito il seguente ragionamento:
Dalla premessa 7:
Smith non è Fuochista.
Dalla premessa 5:
Robinson non è Frenatore: il Sig. Robinson vive a Los
Angeles, quindi non è il passeggero con lo stesso nome del
frenatore.
Dalla premessa 6:
il Sig. Smith vive a Omaha dato che, essendo un fisico
matematico, non può aver dimenticato l'algebra e vive nella
stessa città del frenatore (frequentano la stessa chiesa).
Quindi, dalla premessa 5:
Il Sig. Jones ha lo stesso nome del Frenatore e vive a
Chicago; dunque Jones è frenatore.
Allora,
Smith non è Fuochista e nemmeno Frenatore, quindi è
l'Ingegnere;
Jones è frenatore;
Robinson è fuochista.
Il che coincide anche con il ragionamento seguente:
dato che, "non essendo elencati esattamente nell'ordine",
Smith non è frenatore e dalla 'premessa 7' non è fuochista,
quindi è l'ingegnere.
![]()
229. Problema d'altri tempi
di Severino
Quota nunc hora est? Superest tantum ecce diei quantum bis
gemini exacta de luce trientes.
Valete!
Provo a tradurre:
Che ore sono adesso? Ecco rimangono tante ore (alla fine del
giorno) quante due volte i due terzi delle ore passate.
>>> Risposte & riflessioni
Azarus
La giornata romana è formata da 12 o 24 ore?
Gianfranco Bo
Supponiamo che la giornata sia costituita da n ore e
che ne siano passate x.
Allora ne devono ancora passare n-x.
Perciò:
2*2/3*x = n-x
4/3*x + x = n
7x = 3n
x = 3n/7
Siamo dunque ai 3/7 del giorno.
![]()
228. Copertura del quadrato
di Paolo P.
Dovete inserire un triangolo e 2 cerchi in un quadrato di
lato unitario.
Qual è la superficie massima che riuscite a coprire ?
N.B. Le figure possono essere parzialmente sovrapposte.
>>> Risposte & riflessioni
Paolo P.
Sono arrivato al 92,9 %, ma ho scoperto che si può fare
meglio. Purtroppo credo di aver capito come, ma la ricerca
del massimo richiede troppo tempo (almeno, per me!)
Cesarone
Sovrapponendo le figure, sono arrivato anch'io
a quasi il 93% (dipende dalle approssimazioni). Ho messo un
triangolo con cateti due lati del quadrato, poi un cerchio
grande centrato nel centro del quadrato e un cerchio piccolo
inscritto nella metà del quadrato (triangolone) non occupata
dal primo triangolo. Si ma... integrali, sistemi, ecc.
come dicono nella pubblicità... du' palle!
![]()
227. Il recinto dei monotremi
di Enrico Delfini
Devo dividere il recinto dei miei
ornitorinchi, perfettamente circolare, in quattro parti
uguali per superficie.
Come tutti sanno, gli ornitorinchi, gli echidna e tutti gli
altri monotremi non possono sopravvivere se le recinzioni si
incontrano in modo da formare nodi a quattro
per cui non si può dividere il cerchio con due diametri
perpendicolari.
Qual è il modo più economico (cioè
utilizzando meno rete possibile) per dividere un cerchio in 4
parti equiestese senza che le recinzioni facciano nodi a
quattro ma solo a tre?
Il raggio del recinto è r e per la recinzione sono necessari 4r + 6,28r di rete
Così è molto elegante ma si consuma un sacco di rete.
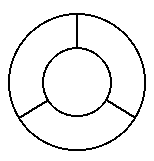
Con quest'altro metodo è possibile utilizzare una rete lunga meno di 4r per la parte interna?
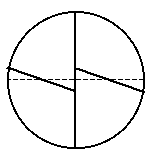
E con il metodo illustrato nella figura qui sotto?

>>> Risposte & riflessioni
![]()
226. Equazione di una qualunque curva?
di Ivo Moretti
Data una una curva (es. un analemma) si può sapere se esiste un'equazione che la descriva?
>>> Risposte & riflessioni
![]()
225. Indovinello linguistico
di Ivo Moretti
Scese e lo picchiarono.
>>> Risposte & riflessioni
Alan Viezzoli
Io direi l'aereo ("picchiare" ha il
significato anche di "scendere in picchiata").
![]()
224. Serie numerica
di Gonario Nieddu
Completare la serie:
6, 3, 8, 4, 10, 5, 12, 6, 14....
la risposta 7 è errata.
>>> Risposte & riflessioni
Silvia Macis, Alan Viezzoli
La mia risposta è 11. Secondo me perchè dopo ogni numero
segue il numero corrispondente delle lettere del precedente e
quindi il numero delle lettere di 14 è 11.
![]()
223. Il povero uccellino tra i due
treni
di Guido
Immaginiamo due treni che viaggiano in direzioni opposte
sullo stesso binario, purtroppo destinati a scontrarsi.
Un uccellino vola da un treno all'altro fino al momento
dell'incidente senza fermarsi mai (appena arriva su un treno
riparte immediatamente).
Supponiamo che i due treni siano inizialmente distanti 120 km
e che viaggino con velopcità costante di 60 km/h;
l'uccellino ha velocità costante di 80 km/h.
E' facile rispondere alla domanda: quanto spazio percorre
l'uccellino?
Un po' meno è rispondere a questa: quanti voli fa
l'uccellino?
E' destinato a essere schiacciato?
>>> Risposte & riflessioni
Cesarone, Enrico Delfini
Si tratta di un paradosso molto simile a quello di
Achille e la tartaruga, in cui pare che la tartaruga non
venga mai raggiunta da Achille. In questo caso potrebbe
sembrare che l'uccellino non venga mai schiacciato dai
due treni.
Prima di tutto rispondo alla prima domanda.
Date le equazioni del moto dei treni, calcolo il tempo che
impiegano per scontrarsi:
Treno 1) x = vt
Treno 2) x = x0 - vt
x : spazio percorso
v = 60 Km/h (velocità treni)
x0 = 120 Km (distanza iniziale)
I due treni si incontrano dopo t secondi:
vt = x0 - vt, allora:
t = 1 h
Questo mi serviva solo per verificare che gli altri tempi non
mi venissero sballati.
Ora, se w è la velocità dell'uccellino e supponiamo
che l'uccellino parta dal primo treno inizialmente, cioè
parta per x = 0, calcoliamo il tempo che impiega per
raggiungere il treno 2:
wt1 = x0 - vt1, dove t1 è il tempo cercato.
t1 = x0 / (w + v) = 6 / 7 h
Nel secondo viaggio, l'uccellino dovrà raggiungere il
treno 1, che avrà già percorso uno spazio vt1. L'equazione
del moto dell'uccellino nel secondo viaggio sarà:
x = wt1 - wt
Il tempo t2 che impiega per raggiungere il treno 1 dal
momento in cui riparte dal treno 2 sarà:
wt1 - wt2 = vt1 + vt2, dove t2 è il tempo cercato.
t2 = t1*(w - v) / (w + v) = 6 / 49 h
Se si prosegue col calcolo dei tempi di ogni viaggio, si nota
che i tempi di ogni viaggio ovviamente diminuiscono sempre più
e sono rappresentati più precisamente da questa formula:
viaggio i-esimo: ti = 6 * (1/7) ^ i
A questo punto supponendo che l'uccellino sia un punto
materiale, quindi di lunghezza infinitesimale, il pedice i va
fatto variare da 1 a più infinito. Per calcolare lo spazio
complessivamente percorso dall'uccellino si può usare
la nota formula:
Sommatoria(y ^ n) = 1 / (1 - y), per n => 0 e per VAL.ASS.
di y < 1.
Nel nostro caso la sommatoria andrà da 1 a infinito:
Sommatoria_da_1_a_infinito( w * 6 * (1/7) ^ i) =
= 480 * ( Sommatoria_da_0_a_infinito( (1/7) ^ i ) - 1) =
= 480 * ( 1 / (1 - (1 / 7) ) - 1 ) = 80 Km,
che è lo spazio cercato.
Per quanto riguarda la seconda domanda:
il numero di voli dell'uccellino è dato dal valore
massimo di i. Quindi l'uccellino compie infiniti voli,
ma sotto l'ipotesi che l'uccellino sia un punto
materiale. Altra ipotesi da fare: il tempo di inversione del
moto deve essere nullo, ma ovviamente questo implicherebbe un
lavoro infinito.
Se facciamo un'ipotesi un po' più realistica di un
uccellino lungo circa 20 cm, allora il poveraccio non
riuscirebbe a completare neppure l'ottavo volo.
Terza domanda:
ovviamente l'uccellino viene schiacciato. Essendo in
teoria infiniti i suoi voli, si potrebbe pensare che esso non
venga mai schiacciato, ma in realtà a un numero di voli
infinito corrisponde anche un tempo di volo via via
decrescente, fino a valori infinitesimi. Questo porta a dire
che la somma dei tempi dei voli sia in realtà finita e LA
MORTE CERTA!
Zapatino
Non è farina del mio sacco, ma invio questa
soluzione che mi pare estremamente più semplice, e che possa
fare al caso di chi non ama i calcoli troppo lunghi...
I due treni si scontrano dopo 1 ora, in quanto hanno una
velocità di 60 km ciascuno e sono distanti 120 km.
Visto che l'uccellino viaggia ad una velocità costante di 80
km/h, l'uccellino avrà percorso 80 km, avendo viaggiato per
un'ora a quella velocità.
Gennaro Cangiano
Questo problema fu posto a Neumann (si scrive così?) il
padre della cibernetica, famoso per la rapidità dei calcoli.
Rispose immediatamente e quando gli chiesero come avesse
fatto, replicò: "Semplice, ho fatto la somma dei tempi
parziali".
Battute a parte, ma qual è il gradiente di velocità
dell'uccellino? Mica vola a velocità costante! Dovrà
frenare quando arriva ad un treno e accelerare quando riparte
verso l'altro.....allora?
![]()
222. L'enigma dei nani
di Paolino89 e Gonario Nieddu
Questo problema è stato posto da Paolino89 al Forum ma una versione molto simile mi era stata inviata in precedenza da Gonario Nieddu, assieme alla soluzione. Per questo motivo ho riportato due autori.
Dieci nani vengono catturati da una tribu di feroci
cannibali che decidono di mangiarli per il pranzo del giorno
successivo.
Il capotribu decide tuttavia di lasciare ai nani una chance
per salvarsi.
Il giorno seguente alla loro cattura, i nani verranno messi
in fila indiana e sul capo di ciascuno verrà messo un
cappello di colore bianco o nero.
Ogni nano, ovviamente, può vedere il colore dei cappelli dei
nani che si trovano davanti a lui ma non il proprio né
quelli dietro.
I nani avranno salva la vita se (a cominciare dall'ultimo
della fila, cioè quello che vede davanti a sé nove
cappelli, fino al primo della fila, che davanti a sé non ha
nessuno) indovineranno il colore del cappello che hanno sulla
testa.
Durante la notte i nani studiano uno stratagemma affinché si
salvino più nani possibile.
La domanda è: qual è il migliore stratagemma e quanti nani
si possono salvare con certezza?
Ricordate che i cappelli non devono essere necessariamente 5
bianchi e 5 neri: la loro distribuzione e proporzione è
assolutamente casuale. Inoltre, durante la cerimonia, i nani
non possono comunicare fra loro. Possono pronunciare, uno
dopo l' altro, solo il colore del proprio cappello. Dopo che
ciascun nano ha pronunciato il presunto colore del cappello,
quelli successivi (sapendo se è stato ucciso o no) sono al
corrente della esattezza o meno della risposta (quindi del
colore effettivo del cappello di quel nano).
>>> Risposte & riflessioni
Enrico
Considerando che i nani in questione siano saggi, onesti,
caritatevoli, buoni, coraggiosi, pronti al sacrificio, che
cioè assomiglino poco agli uomini, possiamo immaginare che
ragionino in modo razionale ed altruista al tempo stesso.
Intendo dire che si comporterebbero in modo da rendere
massimo il beneficio collettivo, anche se ciò comportasse un
piccolo danno personale.
Come primo gradino, propongo questo procedimento:
Numeriamo 1,2,3,...10 i nani: il primo a parlare,10, dice il
colore del cappello in testa a 1; 9 dice il colore in testa a
2, e così fino a 6 che dice il colore di 5. Adesso da 5 a 1,
almeno cinque nani sono salvi. Dei primi cinque,
statiscamente, se ne sono salvati 2 e mezzo.
Ma forse si può fare meglio.
A. P.
Durante la notte si accordano
nero=1
bianco=0
il primo a parlare fa la somma di tutti i cappelli che vede e
dice il resto della divisione per due, 50% di salvezza,
quello davanti a lui somma di nuovo e capisce il colore del
suo cappello (nero se il resto è diverso dall'affermazione
precedente, bianco se uguale), lo stesso fanno quelli
davanti, che hanno tenuto a mente i colori già detti a
partire dal nono.
9 salvi di sicuro, il primo al 50%
^__^
Gianfranco Bo
Molto bello questo problema!
Oggi finalmente ho avuto l'illuminazione, anche se non è
tutta farina del mio sacco ma è dovuta in gran parte ad uno
scambio epistolare che ho avuto di recente, forse con Gonario
Nieddu
Vedo che, come al solito sono ritardatario però la posto lo
stesso perché è leggermente diversa dalle altre.
Complimenti ad Enrico e ad ap. Per ap: la mia soluzione è
simile alla tua nella quale però mi sembra che manchi una
parola???
Dunque...
Il nano in fondo alla fila conta i cappelli bianchi che vede
davanti a sé.
Se il numero è pari, dice "Bianco."
Se il numero è dispari dice "Nero."
Da questo momento in poi tutti i nani possono capire il
colore del proprio cappello man mano che vengono date le
successive risposte.
Supponiamo ad esempio che abbia detto "Bianco".
Se il secondo nano vede un numero pari di cappelli bianchi
vuol dire che il suo è nero, e dice "Nero".
Se invece ne vede un numero dispari, dice "Bianco".
Finché non cambia la parità dei cappelli visti, i nani
successivi diranno sempre "Nero"
Quando cambia la parità dei cappelli visti, il nano in
questione dirà "Bianco"
Ogni volta che viene detto "Bianco" la parità dei
bianchi cambia.
9 nani si salveranno.
Il primo che parla ha il 50%
Ovviamente i nani devono mettersi d'accordo e il primo che
parla deve essere disposto a sacrificarsi.
Gonario Nieddu
Assumiamo bianco=0 e nero=1.
Qualunque sia il numero di prigionieri, il primo a parlare
vede una serie di capelli la cui somma è o pari o dispari.
Se è pari dice "bianco", se è dispari dice "nero".
Il secondo a parlare vedrà anche lui una serie, diminuita di
un elemento. Se la somma resta qualitativamente identica
significa che il suo capello è uno zero (bianco) se cambia
qualità ovviamente il suo capello è un uno (nero).
Il terzo a parlare deve ricordarsi cosa hanno detto il primo
e il secondo, e ragionando sulla qualità della somma vista
da lui capisce che valore ha il suo cappello.
E così via....
![]()
221. Quattro colori in un cerchio
di Sprmnt21
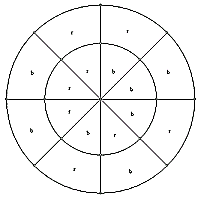
Un cerchio è diviso in 8 settori uguali.
Metà sono colorati di blu e metà sono colorati di rosso.
Un cerchio più piccolo concentrico con il primo è pure
diviso in 8 settori, metà dei quali è colorata di blu e metà
di rosso.
Dimostrare che in qualunque modo siano scelti i settori da
colorare di blu e di rosso, è sempre possibile ruotare il
cerchio piccolo in modo che si abbiano almeno 4 settori
confinanti dello stesso colore.
>>> Risposte & riflessioni
Sprmnt21
Proviamo prima che esistono nei due cerchi due coppie di
colori uguali "equidistanti".
Relativamente ad un dato colore x,
consideriamo nei due cerchi i gruppi di settori consecutivi
monocromatici piu' lunghi. Se in entrambi i cerchi
abbiamo gruppi di settori consecutivi monocromatici piu'
lunghi di uno, abbiamo evidentemente due coppie di settori
contigui di colore x che, a seguito di una opportuna
rotazione, si "corrispondono".
Supponiamo quindi che uno dei due cerchi abbia i settori
colorati nel seguente modo xyxyxyxy.
Se nel secondo cerchio i settori di colore x consecutivi sono
1, 3 o 4 cioe' abbiamo rispettivamente xyxyxyxy, xxx-----
o xxxx----, possiamo mettere in corrispondenza due settori
colorati x "separati" da un settore x-x.
Se invece i settori di colore x consecutivi sono 2, cioe' abbiamo xx------, si verifica facilmente che nemmeno in questo caso e' possibile avere i settori di colore x in posizioni tali che nessuna coppia si corrisponda. Infatti xx-x---- corrisponde a xyx-----(due x a distanza di un settore); xx--x--- e xx---x-- corrispondono a xyxyx--- (due x a distanza di tre settori); xx----x- corrisponde a xyxyxyx- (due x a distanza di cinque settori).
A questo punto ruotando il cerchio piccolo in modo da sovrapporre questedue coppie di settori
--x-x---
--x-x---
si ha che per i restanti sei posti abbiamo 4y+2x colori sopra e sotto, quindi al peggio si avranno due coppie yy sopra e sotto che si corrispondono.
![]()
Sito Web realizzato da Gianfranco Bo