[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Ricreazioni di Ottobre 2001

168. Filo da torcere
proposto da Dino
Un maniaco geometrico vi rapisce e vi porta in mezzo al deserto.
Vi consegna un filo della lunghezza complessiva di 12 metri e un sacco di picchetti (quanti volete). Sul filo sono segnati i metri, ma non i decimetri o i centimetri.
Servendovi dei picchetti dovete formare col filo un angolo di 18° (si suppone che il deserto sia piano).
Tenendo conto che:

1) Non potete lasciare segni di alcun genere sulla sabbia perchè c'è un vento forte e fastidioso;

2) Non potete segnare nulla sul filo anche perchè non avete nulla allo scopo; l'unica concessione è che si possa tenere un segno con le dita solo momentaneamente e non più di un segno alla volta;

3) Potete fissare il filo nella sabbia con i picchetti, non potete lasciare i picchetti sparsi sul terreno o sul filo per tenere il segno; in tal modo dove c'è un picchetto c'è anche il filo fissato;

4) Potete tendere il filo attorno ad un picchetto già fissato precedentemente; in tal modo dove c'è un picchetto oltre ad avere il filo fissato in un certo punto al terreno esso, in un altro suo punto, forma anche un vertice attorno allo stesso picchetto.

Come fate a tracciare l'angolo richiesto?

>>> Risposte & riflessioni
Dino
Premettiano che il lato di un decagono inscritto in un cerchio di raggio pari a due metri è uguale a SQR(5) - 1 e che l'angolo formato dagli estremi di questo lato col centro della circonferenza è pari a 36°.

Detto questo passiamo alla descrizione del metodo per piantare sul terreno due picchetti alla distanza di SQR(5) - 1 e alla costruzione di un angolo di 18° avvalendoci della figura seguente dove sono riportate con colore diverso le varie operazioni da compiere.

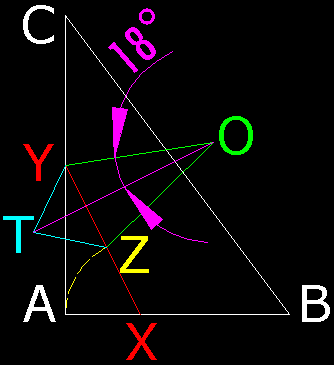
Operazioni disegnate in bianco: poniamo in A l'inizio del filo dato della lunghezza di 12 metri e con esso costruiamo un triangolo rettangolo di cateti lunghi 3 e 4 metri e con l'ipotenusa di 5 metri. Totale del filo utilizzato:

AC + CB + BA = 4 + 5 + 3 = 12

metri. Per costruire questo triangolo basta fissare i due capi del filo con lo stesso picchetto in A dopodicchè fissare, in una direzione qualsiasi, un altro picchetto sulla tacca di 4 metri del filo formando il vertice C, stando ben attenti a tenere la tratta di filo AC ben tesa. Prendiamo, quindi, la tacca 9 metri del filo e lo tendiamo a sua volta ben bene ritrovandoci esattamente nel vertice B dove fisseremo il filo al terreno con un nuovo picchetto. (Per la cronaca questo è uno dei metodi più rudimentali che ancora oggi i topografi utilizzano per poter avere due allineamenti perpendicolari tra loro su un terreno pianeggiante).

Operazioni disegnate in rosso: poniamo due picchetti nei punti X e Y tali che la distanza AX risulti pari ad 1 metro (dunque il picchetto va sulla tacca 11 metri) mentre la distanza AY risulti pari a 2 metri (picchetto giusto sulla tacca di 2 metri); in tal modo la distanza XY risulterà sicuramente pari a SQR(5) essendo per il teorema di Pitagora:

XY² = AX² + AY² = 1² + 2² = 1 + 4 = 5

Togliamo poi i picchetti in C e in B, e tendiamo la parte della corda YCBX per formare l'ipotenusa del triangolo rettangolo AYX: il tratto teso risulterà più lungo del dovuto, ma l'importante che passi per XY. Togliamo momentaneamente il picchetto in X tenendo il filo col dito nel punto suddetto in modo da rifissarlo successivamente col picchetto tolto ottenendo il triangolo AYX. In questo modo abbiamo utilizzato solo un tratto di filo lungo, in metri, a:

AY + YX + YA = 2 + SQR(5) + 1 = 3 + SQR(5)

Operazioni disegnate in giallo: svincoliamo definitivamente il picchetto posto in A e facendo perno sul picchetto X, portiamo il tratto XA fissandolo su XY nel punto Z con un nuovo picchetto. Ora ZX è precisamente 1 metro, essendo uguale ad AX, e quindi YZ risulterà pari a SQR(5) - 1.

Operazioni disegnate in azzurro: a questo punto togliamo anche il picchetto nel punto X e tendiamo 1 metro di filo da Y ed 1 metro di filo da Z unendoli. Per fare ciò possiamo sfruttare i 2 metri di filo che escono da Y (in direzione A), mentre occorrerà portare una misura intera del filo nel punto Z (la tacca immediatamente prossima è quella di 4 metri, per cui sfilando dal terreno il picchetto in Z e tenendo momentaneamente il segno sul filo con le dita accosteremo la tacca dei 4 metri al punto trovato ed in esso ricollocheremo nuovamente il picchetto tolto) e far ruotare da questa una misura incrementata di 1 metro (tacca di 5 metri). Uno dei due punti d'incontro lo indicheremo con T. Fissiamo in T, con un picchetto sul terreno, la parte di filo che esce da Z, mentre teniamo liberi i 2 metri di filo che escono da Y.

Operazioni disegnate in verde: tendiamo ancora 2 metri di filo da Y e 2 metri di filo da Z unendoli come fatto precedentemente. Per fare ciò possiamo far ruotare l'inizio di filo, che avevamo indicato con A, intorno ad Y (essendo per costruzione la distanza AY proprio uguale a 2 metri), mentre occorrerà tendere l'altra estremità del filo dal punto T (tacca 5 metri), farla girare attorno al picchetto Z (tacca di 6 metri) ed incrementarla di altri 2 metri (arrivando alla tacca di 8 metri). Uno dei due punti d'incontro, quello opposto a T, lo indicheremo con O e l'angolo YOZ sarà di 36° per quanto detto nella premessa.

Operazioni disegnate in fucsia: non ci resta che tracciare la bisettrice dell'angolo YOZ e per fare ciò picchettiamo il punto O solo dal lato del filo di Y (cioè sulla tacca di 0 metri); dall'altro capo recuperiamo il filo fino al punto T, dov'è ancora saldamente fissato al terreno (alla tacca 5 metri), dopodicchè tendiamo il filo proprio dal picchetto T a quello O. L'angolo TOY misura, per costruzione, esattamente 18° come richiesto!

Volendo formare detto angolo su una porzione di filo continua occorre ripicchettare il punto O sul filo uscente da T (basta quindi sfilare quello precedente, tenere un attimo il segno con le dita e ripicchettarlo sulla nuova tratta di filo). Ora da O tendiamo il filo in direzione Y ed il gioco è fatto! La lunghezza del filo ci consente anche di andare oltre Y per una maggiore comodità del picchettamento e per poter sbloccare successivamente e definitivamente il picchetto Y (invece non occorrerà mai sbloccare l'ultimo picchetto messo, quello riposto in O e quello in T).

Ivan Furlan
Parto dall'idea che 18° = 90°/5. Si deve quindi riuscire a ricavare la quinta parte di un angolo di 90°.


Passo 1: corda segnata ogni metro

Attenzione curare che i picchetti siano bene allineati e che l'angolo sia di 90°. Un angolo di 90° si
può fare anche ad occhio abbastanza preciso. Si potrebbe anche costruire usando la corda ed i picchetti
ma per abbreviare la soluzione tralascio questa parte.

Passo 2

pianto un picchetto in un altro luogo e lego la corda come mostrato (tengo il filo teso con una mano):

Passo 3

Traccio un ¼ di cerchio usando il metro di corda come compasso ed i picchetti per marcare il cerchio
(più picchetti si mettono meglio è, ideale infiniti picchetti, bisogna tenere ben teso il filo):

Passo 4

Stacco la corda dal centro e misuro il ¼ di cerchio con la corda, legando prima la corda al picchetto indicato facendo quindi aderire la corda bene sull'arco. Tengo infine con una mano il segno e slego la corda.:

Passo 5

Lego la corda al picchetto indicato a seguito avendo cura di non perdere il segno della lunghezza arco.

Curo di posare in modo parallelo la corda ad i tre picchetti posati sul lato destro ad essa.

Passo 6

Marco la lunghezza dell'arco di cerchio con un picchetto, togliendo ora la corda mi trovo nella situzione seguente:

Passo 7

Lego le due stremità della corda come segue e passando per i picchetti come indicato trovo un vertice, dove metterò un altro picchetto:

Passo 8

Libero la corda e la tendo bene tra il vertice trovato e il picchetto indicato, affrancandola in modo che resti diritta:

Passo 9

Faccio quindi passare la corda attorno i picchetti come segue (immagine ingrandita):


Tengo quindi la misura tra l'incrocio e il picchetto di „partenza misura" con le mani, essa equivale ad 1/5 di circonferenza precedentemente segnata con i picchetti. Riportando come segue sulla circonferenza e unendo l'arco ottenuto con il centro della circonferenza si ottiene l'angolo di 18° voluto.

Gianfranco Bo
Il problema è interessante e metto anch'io qualche soluzione poco ortodossa, come segno che ci ho pensato...

1) Con la trigonometria: visto che tan(18°) = 0,32... basta costruire (fissando opportunamente i picchetti) un triangolo rettangolo di cateti 3 e 9. Un angolo acuto misurerà 18,43 °, dài è quasi 18°! ;-) Questa procedura, comunque può essere resa più precisa e credo possa essere realizzata con le condizioni che hai posto.

2) Con il Sole: utilizzando un picchetto e un pezzo di corda costruisco un pendolo di lunghezza nota del quale posso calcolare il periodo di oscillazione. Me ne sto fermo a far oscillare il pendolo ed utilizzo la mia ombra per piantare opportunamente dei picchetti. Quando è passato un tempo opportuno la mia ombra avrà ruotato di 18°. Naturalmente bisogna acquisire alcune informazioni astronomiche e studiarci un po' su.

3) Con qualche centinaio di picchetti: fisso un raggio noto con la corda e costruisco un arco di cerchio lungo come il raggio piantando i picchetti uno attaccato all'altro. Otterrò l'angolo di un radiante = 57,3°. Conto i picchetti, faccio una proporzione e individuo un angolo di 18° circa.

167. Due poesie
proposto da Giorgio Dendi
Ti scrivo due brevi poesie di due miei amici: ti invito a leggerle e a rileggerle attentamente... poi ti farò una domanda.

La signora della porta accanto
Siccome mi avean detto che batteva,
mi sono fatto sotto e a onor del vero,
mi son spogliato nudo in un baleno:
ci credereste che mi ha fatto nero?

Il vino
Se dal buon corpo come dal colore
risulta un bel carattere deciso,
si può finire col giustificare
che si tratta di un DOC ch'è da salvare.

A questo punto se ti facessi la domanda, sarebbe facile rispondermi, allora ti invito a fare la domanda che dovrei fare io, e poi puoi risponderti.
Buon lavoro.
Giorgio Dendi

>>> Risposte & riflessioni
Gianfranco Bo
La seconda potrebbe avere un altro titolo: il documento word.

Alberta Sestito
La prima potrebbe avere un altro titolo: il sole.

166. Numeri digitali
proposto da Dino
Le dieci cifre in un'orologio digitale sono:

In tutto sono 49 linette.

E' possibile allora sistemare le dieci cifre, ammettendo anche eventuali rotazioni e/o ribaltamenti delle stesse, a formare una griglia quadrata 5·4 come quello di figura che, come si può verificare, ha anch'esso 49 linette?

>>> Risposte & riflessioni
Alberta Sestito

165. A volte ritornano
proposto da Sprmnt21

Un punto M, che sta all'interno di un triangolo ABC, si muove lungo la parallela a BC fino ad incontrare CA, a questo punto si muove lungo la parallela ad AB fino ad incontrare BC, quindi si muove parallelamente a CA e cosi' via.

Provare che M ritorna nella sua posizione iniziale.

>>> Risposte & riflessioni
N.d.R. Poiché la soluzione di Giovanni Macchia è piuttosto articolata, ho aggiunto un disegno. Se ci sono errori nel disegno prego di segnalarmelo.

Giovanni Macchia
Consideriamo il triangolo ABC come l'intersezione di 3 rette, la retta AB, la retta AC e la retta BC. Consideriamo il punto B come origine di un sistema di coordinate cartesiane. Pertanto B== (0,0), A== (xa,ya), C==(xc,0). Indichiamo le coordinate di M == (xm,ym).La retta AB ha equazione

(1) y=(ya/xa)x,

la retta AC ha equazione

(2) (y-ya)/(x-xa) = -ya/(xc-xa)

la retta BC ha equazione y=0 e la retta per M parallela alla retta BC è

(3) y=ym

M intersecherà la retta AC nel punto di coordinate P == (x',ym ) con
x' = (-ym*xc+ym*xa+ya*xc )/ya

M prosegue parallelamente ad AB fino ad intersecare la retta BC. Descrive una retta con lo stesso coefficiente angolare di (1) passante per il punto (x',ym). Sostituendo le coordinate del punto P nella equazione di una generica retta parallela ad AB y = (ya/xa)x +n, si ha

ym = (ya/xa) (-ym*xc+ym*xa+ya*xc )/ya +n
da cui
n = (ym-(-ym*xc+ym*xa+ya*xc )/xa))= (ym*xc-ya*xc)/xa

e quindi l'equazione della retta è

y = (ya/xa)x +(ym*xc-ya*xc)/xa


che interseca la retta BC nel punto di coordinate P' == ((-ym*xc+ya*xc)/ya,0). La retta parallela ad AC e passante per P' ha lo stesso coefficiente angolare della (2) e la sua generica equazione è

(4) y = -ya/(xc-xa) x + n

Sostituendo in (4) la coordinata P' si ha

n =(-ym*xc+ya*xc)/(xc-xa) e quindi la (4) diventa

y = -ya/(xc-xa) x + (-ym*xc+ya*xc)/(xc-xa)

L'intersezione con la (1) avviene in nel punto P'' di ascissa x'' tale che

(ya/xa)x'' = -ya/(xc-xa) x + (-ym*xc+ya*xc)/(xc-xa)

e ordinata y'' = ya-ym. Se ya=2* ym, allora la retta parallela a BC passante per y''=ym passa ovvamente per M.

Consideriamo il caso in cui ya¹2* ym e la retta passante per P'' e parallela a BC ha quindi equazione

y = ya-ym

ed interseca la retta AC nel punto P''' == ((ym*(xc-xa)+ya*xa)/ya, ya-ym).

Tracciamo la retta parallela ad AB e passante per P'''. Si ottiene

(5) y = (ya/xa) x -(ym*xc )xa

che interseca BC nel punto P''''== ((ym*xc/ya, 0). Tracciamo ora una retta passante per P'''' e parallela ad AC. Essa ha equazione


(6) y = -ya/(xc-xa) x + (-ym*xc)/(xc-xa)

L'intersezione di (6) con la retta AB è data dal punto P''''' di coordinate (ym*xa/ya,ym) (Basta procedere sostituendo in (6) la y=(ya/xa)x, calcolando x e quindi y). Pertanto, la retta successiva parallela a BC ha equazione y=ym e passa quindi per M, che ha ordinata ym

164. A teatro
proposto da Renè
Ho bisogno di aiuto.
Vi espongo questo problema sperando nella soluzione.
In un teatro vi sono due ordini di posti, per i primi si paga £30.000 e per i secondi si paga £19.000.
In uno spettacolo in cui tutti i 640 posti furono occupati, l'incasso fu di £14.470.000.
Calcolate il numero dei primi posti e quelli dei secondi posti.

>>> Risposte & riflessioni
Soluzione semplice-semplice.

Sia x il numero dei primi posti.
Allora (640-x) è il numero dei secondi posti.

Possiamo scrivere l'equazione:

30.000x + 19.000(640-x) = 14.470.000
30.000x + 12.160.000 - 19.000x = 14.470.000
11.000x = 2.310.000
x = 210

Per risolvere il problema senza utilizzare le equazioni si può ragionare così:

Se tutti i posti costassero 30.000 allora l'incasso sarebbe:
30.000 * 640 = 19.200.000

Ma l'incasso è inferiore e per la precisione la differenza è:
19.200.000 - 14.470.000 = 4.730.000

Questa differenza è dovuta al fatto che un certo numero di posti costa meno e per la precisione costa 11.000 meno degli altri.
Quanti sono questi posti?
4.730.000 / 11.000 = 430 (numero dei secondi posti)
640 - 430 = 210 (numero dei primi posti)

163. Riflessioni sul paradosso dei Cretesi
proposte da Gianvittorio Solari
Il paradosso del mentitore (o di Epimenide o dei Cretesi)
Epimenide diceva: Tutti i Cretesi sono mentitori"
Epimenide, che era Cretese, diceva la verità?

Premessa: cos'e' la verita? o meglio quando qualcosa contiene la verità?
Problema filosofico annoso. Tanto che la verità possiamo dividerla in due grandi categorie
verità e Verità.
La prima appartiene all'esser-ci (concetto heidegeriano) la seconda appartiene all'astrazione (come il punto geometrico)

verità delleser-ci

Un popolo vive in una valle dove scorre un fiume dalla quale nessuno mai si è mosso. (tipo mito della caverna). Un abitante si mette in viaggio e va oltre le montagne.
Al suo ritorno racconta che al di là delle montagne scorre un altro fiume. La verità della cosa in questo caso dipende dal grado di fiducia che il popolo ha nei confronti del abitante viaggiatore. Se la fiducia è cieca avremo una Verità (tipo verità rivelata).

Il grado massimo lo avremo se tutto il popolo si metterà in viaggio e verificherà l'effettiva esistenza del fiume. Se lui avrà mentito nascerà un popolo "scientifico". Si laicizzerà in sostanza.

Veniamo ai cretesi.

secondo me poichè l'afferamazione ha come sua base "ontologica" la verità, il paradosso posto nei termini in cui è esso stesso posto, impone che chi fà l'affermazione non  che dire " tutti i cretesi sono bugiardi". Ossia , e questo è il punto più delicato, la valutazione "morale" dell'ascoltatore dipende da chi afferma senza poterne accertare il contenuto.
quindi se è vero che in "ASSOLUTO" tutti i cretesi sono bugiardi il cretese per essere esso stesso un bugiardo deve dire la verità. Ossia:

Tutti i cretesi sono bugiardi? ( cosa che diamo per "assolutamente" vera )Ma tu hai detto la verità e sei cretese quindi hai mentito.Quindi per colpa di Epimenide ( se vogliamo solamente legato al Tempo dell'affermazione )tutti i cretes sono dei bugiardi,comunque.
Questo per dimostrare una cosa:
L'irrisolvibilità di certi paradossi dipende dall'essere storico dell'uomo che come essere finito ha una doppia natura di relativismo tendente all'assoluto. Ma quest è un'altra storia....

Si potrebbe obbiettare:

il paradosso dei cretesi è indecidibile.
Ossia: se è vera la prima non è vera la seconda e viceversa.
L'obbiezione è in parte, ma solo in parte, valida se partiamo dai presupposti della logica formale.
Cioè se svuotiamo il paradosso dei suoi contenuti e di altri elementi altrettanto fondamentali.

Innazitutto chi parla è Epimenide e non un picopallino qualunque ( situazione soggettiva).
Le due affermazioni non sono disgiungibili: il paradosso è un  tuttuno.
Quando inventiamo un gioco linguistico ( Wittgenstein ) come è il caso di un paradosso o altro, creiamo qualcosa che non è più disinnescabile. Un determinato orizzonte è un unico composto dai suoi elementi e nessuno di essi è trascurabile.
La domanda che ci dobbiamo porre nel "decidere" ( nel suo significato più forte ) è non dove stia la verità del paradosso ma bensì: chi decide che un intero popolo sia bugiardo? epimenide? o forse una squadra di sociologi, psicologi che parte per Creta e fa le sue indagini in base a delle categorie di pregiudizi?
Ammettiamo per assurdo che questo sia vero ( i cretesi sono tutti bugiardi) , allora qualunque affermazione da parte di ciascuno di loro sarà sempre una bugia qualunque cosa essi dicano.Perchè nessuno gli crede ( si pensi anche al mito di Cassandra ).
Come detto nel precedente messaggio, se Epimenide è cretese allora dice la verità con la seconda affermazione  ( lui è cretese ) e quindi mente sul fatto che siano tutti bugiardi. Lo stesso vale quando fa la prima affermazione : dice la verità e si contraddice. E quindi finisce nella schiera dei suoi isolani. Tutti i cretesi sono bugiardi.
vale appena accennare che se Epimenide non è Cretese il paradosso è solo una stupidaggine.
In teoria , ma solo in teoria, per chi ascolta è sufficiente scoprire se Epimenide è cretese per sapere se i cretesi sono tutti bugiardi. se lo è allora sono bugiardi se non lo è allora avremo avuto a che fare con un possibile diffamatore.

L'aspetto problematico della questione è questo.
Il paradosso mette insieme due cose che non pssono stare insieme.
L'essere cretese di Epimenide è una verità puramente materiale, semplice e finita: lui è nato a Creta oppure no. Punto.
L'affermare che qualcuno è un bugiardo è tutto un altro paio di maniche perchè si crea una situazione che comporta una infinita serie di variabili.

Heidegger diceva: Non cercare la soluzione della domanda. Il problema è : perchè mi faccio questa domanda? Il perchè del perchè.
Quello di epimenide viene considerato un paradosso da chi crede in unica verità per cui pensa che vi possa essere da qualche parte una riduzione formale che lo risolva. Invece molto probabilmente ( io dico sicuramente ) non esiste.

>>> Risposte & riflessioni

Sito Web realizzato da Gianfranco Bo