[BASE Cinque - Appunti di Matematica ricreativa]
Alcuni dei problemi discussi da Ulam, Banach, Mazur, Steinhaus, Ruziewicz & C. nel mitico Scottish Café, a Lwow (Leopoli) - Polonia, nel 1935
Noi ne abbiamo risolto solo due!
Grazie a Mathmum, Pasquale, Daniela, Franco, Panurgo, Ivana.
Problema 19. (Ulam)
Un solido di densità uniforme che galleggia sull'acqua rimanendo in equilibrio in ogni posizione è una sfera?

Problema 21. (Ulam)
E' possibile ottenere la superficie di un toro applicando al disco x2+y2 <= 1 delle trasformazioni aventi controimmagini arbitrariamente piccole?
(cioè per ogni e > 0 deve esistere una trasformazione f(p) del disco nel toro, tale che, se |p1-p2| >= e allora f(p1) /= f(p2).

Problema 38. (Ulam)
Siano dati N elementi (persone).
A ciascun elemento ne associamo altri K scelti a caso fra gli N dati (sono gli amici di una data persona).
Qual è la probabilità PkN che da ciascun elemento si possa raggiungere ogni altro elemento attraverso una catena di amici?
La relazione di amicizia non è necessariamente simmetrica!
Trovare
lim PkN
n->inf
La risposta è 0 oppure 1?

Definizione di un gioco - Mazur
Sia dato un insieme E di numeri reali.
Viene quindi definito un gioco tra due giocatori, A e B avente le seguenti regole:
A seleziona un intervallo arbitrario d1, quindi B seleziona un segmento (intervallo) arbitrario d2 contenuto in d1.
Al turno successivo A seleziona un intervallo arbitrario d3 contenuto in d2, e così via.
Il giocatore A vince se l'intersezione di d1, d2, ..., dn contiene un punto dell'insieme E, in caso contrario A perde.
...e qui mi fermo, perchè non mi è chiaro il tutto. L'insieme E è noto ai giocatori? cosa diamine è la "first category"? perchè se per first category si intendesse il primo intervallo scelto, allora il complementare di E non può contenere alcun punto dell'intervallo, e di conseguenza nessun punto dell'intersezione tra questo intervallo e qualunque suo sottointervallo... Lascio a voi la patata bollente. Io non sono all'altezza, al momento (forse, con un anticipo sulla bottiglia di vino in premio...)
Anche nella variante dice che "E vince se il numero formato da tali cifre....." ma E è l'insieme, non un giocatore.
Qui c'è chiaramente un "typo", un errore di battitura...

...

Problema 59. (Ruziewicz)
Si può scomporre un quadrato in un numero finito di quadrati tutti diversi?
Una risposta a questo problema si trova in: Martin Gardner, Enigmi e giochi matematici, vol II, Sansoni, pp. 151-170.

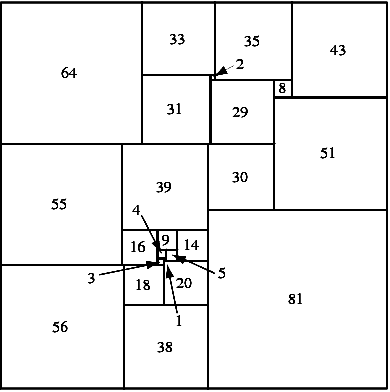
Scomposizione di un quadrato in 24 quadrati diversi.
Il record attuale (2008) è il quadrato del 21° ordine.
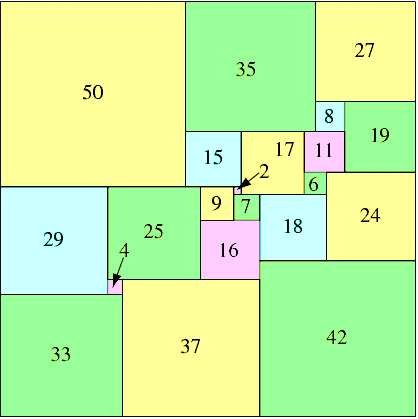
Scomposizione di un quadrato in 21 quadrati diversi.
Il lato del quadrato grande è 112 unità.
I numeri nei vari quadrati indicano la misura dei rispettivi lati.

E' possibile, per ogni e > 0, rappresentare la superficie di una sfera come somma di un numero finito di regioni infinitamente piccole, chiuse, connesse e senza punti interni in comune? Si assumano, quali frontiere di tali insiemi:
(a) poligoni
(b) curve di lunghezza finita
(c) insiemi aventi misura nulla

Problema 123. (Steinhaus)
Siano dati tre insiemi A1, A2, A3, nello spazio euclideo tridimensionale con misura di Lebesgue finita.
Esiste un piano che divide ciascuno dei tre insiemi A1, A2, A3, in due parti, aventi uguale misura?
Generalizzare il problema con n insiemi in spazi a dimensione n.

Problema 147. (Mazur)
Supponiamo che una palla da biliardo venga lanciata con un angolo di 45° a partire da un angolo di un biliardo rettangolare e i cui lati hanno un rapporto razionale.
Dopo un numero finito di rimbalzi sulle sponde, la palla finirà in uno dei tre altri angoli?
Nota: Panurgo ha inviato la seguente soluzione al Forum (6 agosto 2008).
Consideriamo un tavolo da carambola (così evitiamo di discutere sulle dimensioni delle buche ecc.) di lati a e b con a < b: con questa assunzione non si ha perdita di generalità perché lo scambio di a con b
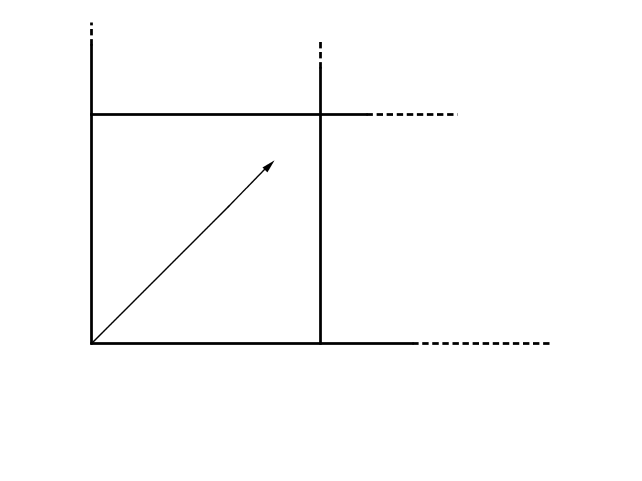
equivale a iniziare il moto della palla dall'altro angolo adiacente al lato corto
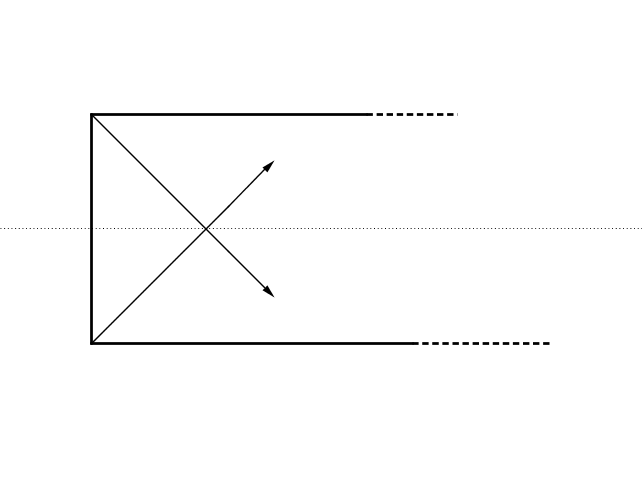
e il piano del biliardo possiede un piano di simmetria perpendicolare passante per l'asse dei lati corti che rende equivalenti le due situazioni. Prendiamo due numeri interi, m e n tali che m/n = a/b con m/n frazione ridotta i minimi termini, come misure del piano del biliardo. Dato che il moto è a 45°, la palla percorre distanze eguali longitudinalmente e trasversalmente e al primo rimbalzo colpisce la sponda del lato lungo ad una distanza m dal lato corto
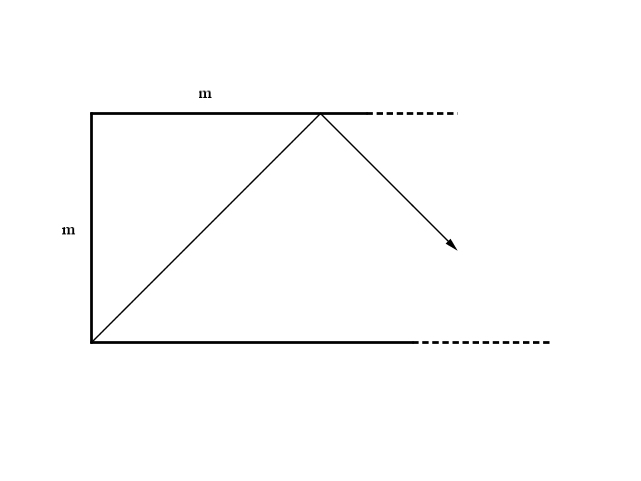
Al secondo ribalzo la palla colpisce la sponda opposta ad una distanza di 2m, al terzo, di 3m, e così via fino a che la distanza del rimbalzo dal lato corto successivo non sarà r < m
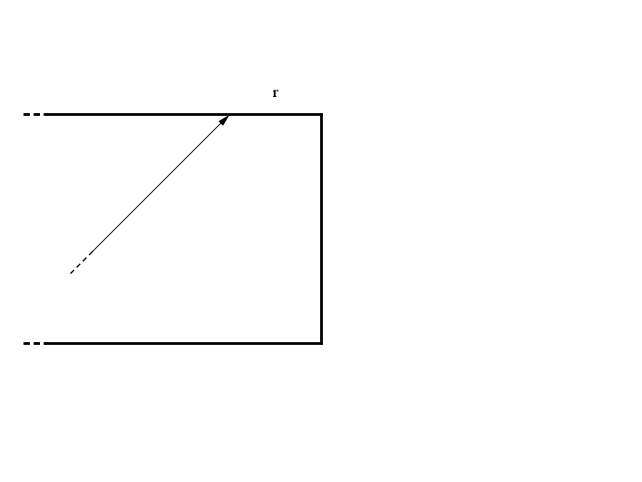
La palla esegue, col suo moto, una divisione col resto: n = q × m + r.
A questo punto la palla rimbalza prima sul lato corto e poi sul lato lungo, procedendo in verso opposto.
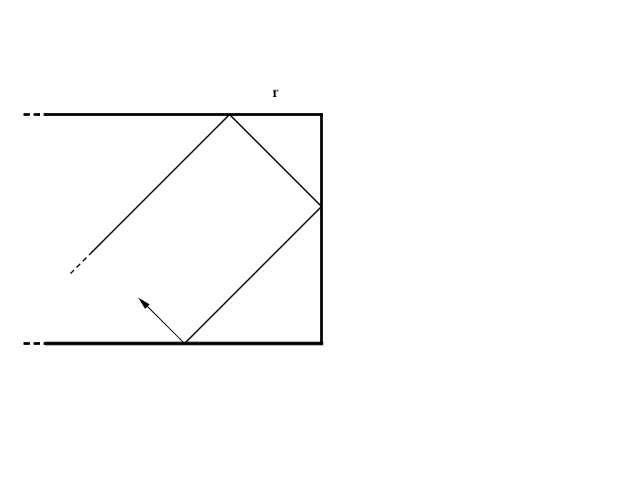
Ma, se noi poniamo al posto della sponda uno specchio (elastico!) vedremo l'immagine riflessa della palla che prosegue la sua corsa sul biliardo speculare.
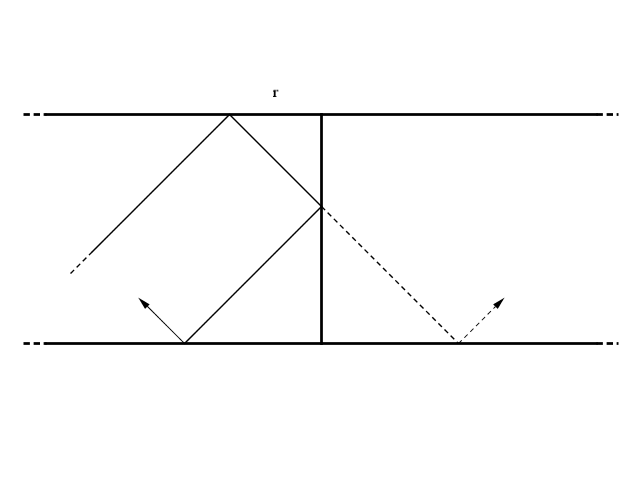
E se lo specchio fosse proprio lo Specchio di Alice, sarebbe la palla (e non la sua immagine) che continuerebbe la corsa. Ed ecco che, dopo altri q rimbalzi arriverebbe alla distanza 2r dal lato corto successivo (precedente?)
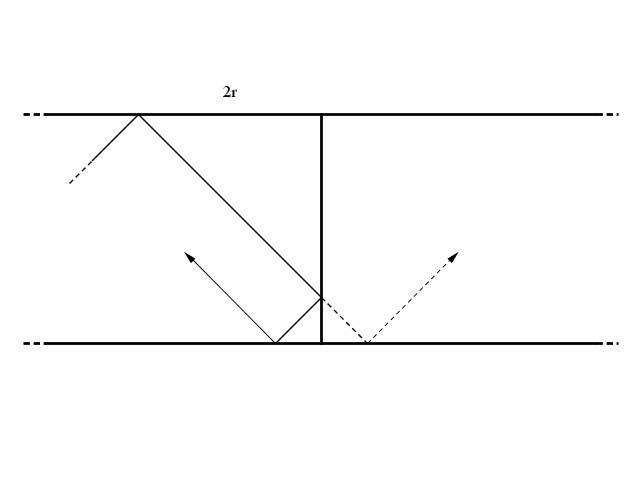
Non volendo invertire il moto della palla abbiamo sostituito anche questa sponda con uno Specchio di Alice: la palla procederà per altri q rimbalzi fino ad un punto posto a 3r di distanza dal prossimo lato corto/Specchio di Alice.
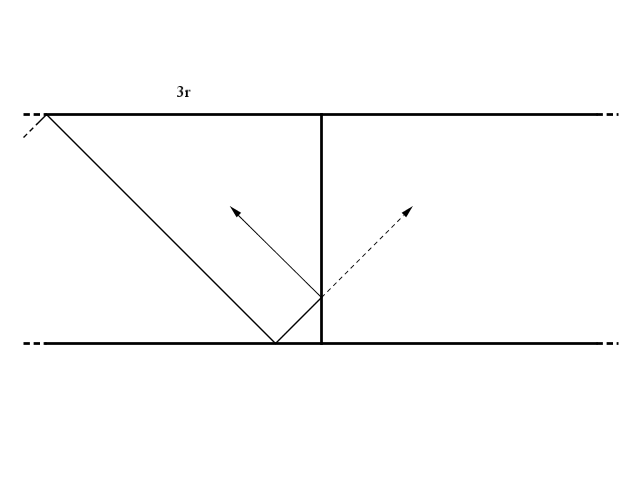
Prima del primo specchio, r, prima del secondo, 2r, prima del terzo, 3r e così via fino a che, finalmente, prima dell'm-esimo specchio la distanza sarà mr e la palla raggiungerà l'angolo con esattamente r rimbalzi. Vediamo un esempio con m = 5 e n = 7.
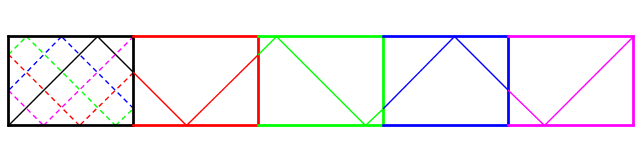
Le traiettorie sui vari tavoli riflessi e traslati (ovvero, doppiamente riflessi) sono riportate sul tavolo originale con tratteggio.
La palla subisce m (contando l'ultima nell'angolo) Riflessioni di Alice e compie m × q + r = n rimbalzi sui lati lunghi (ho fatto un esempio con q = 1 altrimenti il disegno veniva troppo lungo e stretto).
Per capire quale sarà l'angolo colpito sovrapponiamo al piano del biliardo un reticolo unitario (unità di misura di m e n).
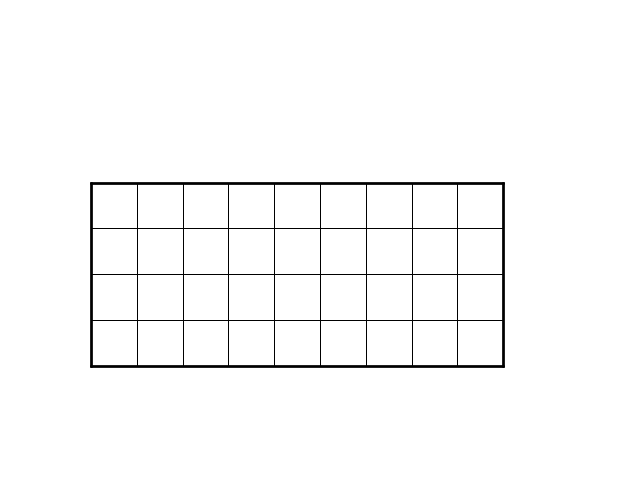
La palla, muovendosi a 45°, non può spostarsi che in punti del reticolo in cui la variazione delle due coordinate sia uguale (in modulo), cioè punti di "parità" uguale.
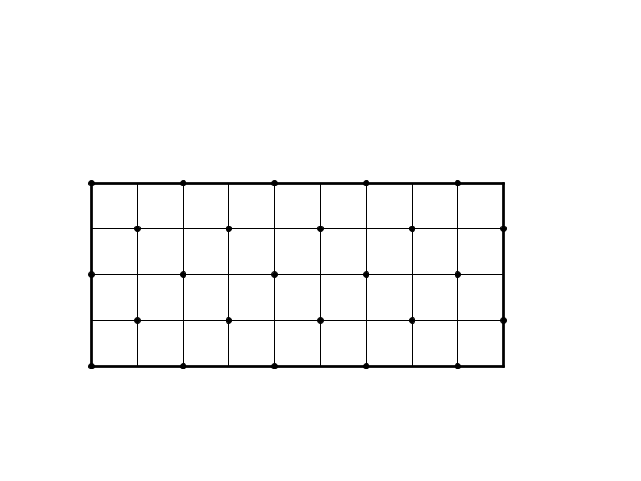
Quindi verrà raggiunto l'angolo di parità uguale: nella figura precedente il lato lungo è dispari e il lato corto è pari, nella figura successiva è vero il contrario.
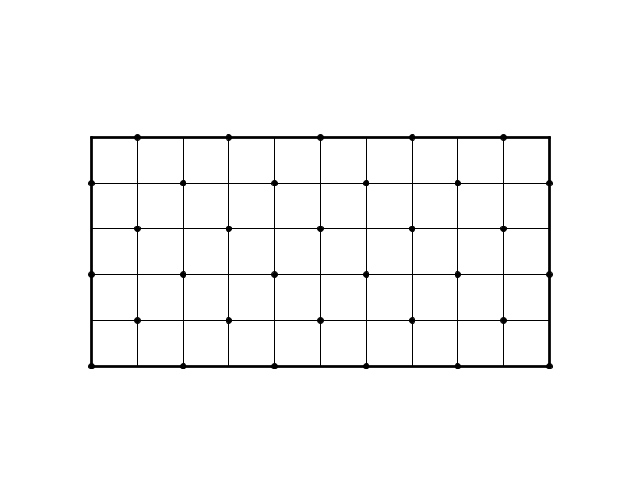
Se uno dei due lati è pari l'angolo di parità uguale è l'angolo adiacente al lato pari; se i due lati sono entrambi dispari, l'angolo di parità uguale è l'angolo opposto al centro.
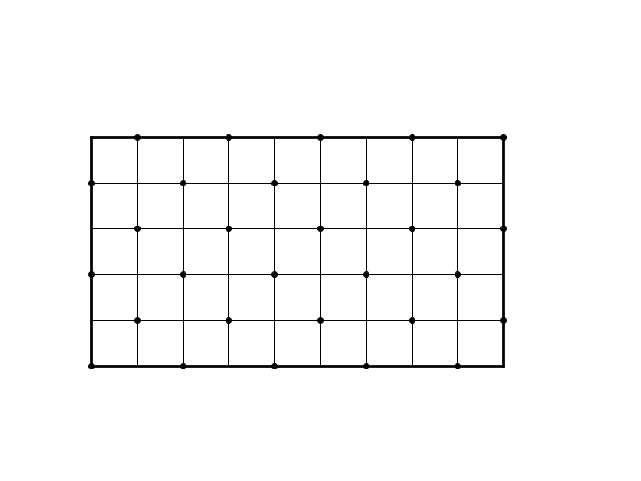
Tertium non datur: m e n non possono essere entrambi pari altrimenti la frazione non è ridotta ai minimi termini contro le ipotesi.
Nota: Franco ha inviato la seguente soluzione al Forum (4 agosto 2008).
Avevo pensato di dimostrarlo graficamente con l'ausilio di questo disegno:
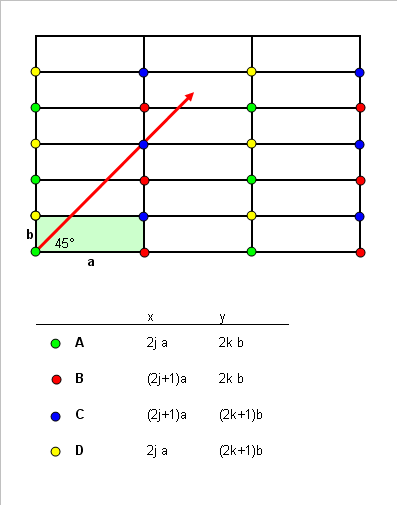
Se i lati sono in rapporto razionale a/b (con a>b) la biglia finisce in una buca rimbalzando a-1 volte sulla sponda lunga e b-1 volte sulla corta.
Se a e b sono entrambi dispari la biglia finirà nella buca C (blu).
Se a è dispari e b pari finirà nella buca B (rossa).
Se a è pari e b dispari finirà nella buca D (gialla)
N.B. Naturalmente è impossibile che la biglia torni alla buca A (verde) di partenza!
Ulteriori precisazioni.
Provo ad esporre più chiaramente il mio ragionamento.
Intanto se il rapporto fra i due lati è un razionale a/b posso utilizzare un'opportuna unità di misura tale per cui i lati del biliardo misurino appunto a e b. (Il fatto che nel precedente post avessi indicato a>b serviva solo ad identificare le due sponde come lunga e corta ma in realtà è assolutamente irrilevante).
Le coordinate delle "famiglie" delle 4 buche A, B, C e D, ottenute per riflessioni successive del biliardo rispetto alle sponde sono quelle che avevo indicato nella figura:
A: x=2ja ; y=2kb
B: x=(2j+1)a ; y=2kb
C: x=(2j+1)a ; y=(2k+1)b
D: x=2ja ; y=(2k+1)b
con j e k interi.
La traiettoria della biglia (a 45° partendo dall'origine) è rappresentata dalla retta y=x.
Se sia a che b sono dispari allora esistono sicuramente una coppia di j e k tali che risulti (2j+1)a=(2k+1)b in particolare i valori minimi saranno j=(b-1)/2 e k=(a-1)/2. La biglia finirà nella buca C.
Se a è pari e b dispari allora esistono sicuramente una coppia di j e k tali che risulti (2j+1)a=2kb in particolare i valori minimi saranno j=(b-1)/2 e k=a/2. La biglia finirà nella buca B.
Se a è dispari e b pari allora esistono sicuramente una coppia di j e k tali che risulti 2ja=(2k+1)b in particolare i valori minimi saranno j=b/2 e k=(a-1)/2. La biglia finirà nella buca D.

Problema 152. (Steinhaus)
Un disco di raggio 1 ricopre almeno due punti, aventi coordinate intere (x,y), con x <= 5, y <= 5.
Se al disco vengono applicate delle traslazioni di vettore n × w, con n = 1, 2, 3, ... e tale che il vettore w abbia entrambe le componenti irrazionali, a rapporto irrazionale, allora i numeri 2, 3, 4 si ripetono indefinitamente.
Qual è la frequenza di tali eventi per n -> ∞ (infinito)? Tale frequenza esiste?
(per il calcolo della frequenza: 100 grammi di caviale) (per la dimostrazione dell'esistenza della frequenza: una birra piccola)
Aggiunta della mathmum: per chi lo traduce meglio di me o comunque ne capisce il significato, offro io un piatto di spaghetti con bottarga e zucchine
---
Immagina di avere il disco in questione in una posizione arbitraria all'interno di un reticolo di passo 1: il disco coprirà 2, 3, 4 o 5 punti. Se lo trasli per esempio del vettore ((0,0), (1,1)) il disco coprirà lo stesso numero di punti della posizione precedente.
Viceversa, un vettore di componenti irrazionali a rapporto irrazionale porta sicuramente, a furia di traslazioni, a coprire un numero di punti diverso dalla posizione precedente...
---

Problema 193. (Steinhaus)
Nota: più sotto c'è la traduzione in italiano.
What follows is the preface to a typed document entitled "The Scottish Book" sent by Stan Ulam from Los Alamos to Professor Copson in Edinburgh on January 28 1958.
PREFACE
The enclosed collection of mathematical problems has its origin in a notebook which was started in Lwow, in Poland in 1935. If I remember correctly, it was S Banach who suggested keeping track of some of the problems occupying the group of mathematicians there The mathematical life was very intense in Lwow Some of us met practically every day, informally in small groups, at all times of the day to discuss problems of common interest, communicating to each other the latest work and results. Apart from the more official meetings of the local sections of the Mathematical Society (which took place Saturday evenings, almost every week!), there were frequent informal discussions mostly held in one of the coffee houses located near the University building - one of them a coffee house named "Roma" and the other "The Scottish Coffee House". This explains the name of the collection. A large notebook was purchased by Banach and deposited with the headwaiter of the Scottish Coffee House, who, upon demand, would bring it out of some secure hiding place, leave it at the table, and after the guests departed, return it to its secret location.
You can see a picture of the Scottish Café.
Many of the problems date from years before 1935. They were discussed a great deal among the persons whose names are included in the text, and then gradually inscribed into the "book" in ink. Most of the questions proposed were supposed to have had considerable attention devoted to them before an "official" inclusion into the "book" was considered. As the reader will see, this general rule could not guarantee against an occasional question to which the answer was quite simple or even trivial.
In several instances, the problems were solved, right on the spot or within a short time, and the answers were inscribed, perhaps some time after the first formulation of the problem under question.
As most readers will realize, the city of Lwow, and with it the "Scottish Book", was fated to have a very stormy history within a few years of the book's inception A few weeks after the outbreak of World War II, the city was occupied by the Russians. From items at the end of this collection, it will be seen that some Russian mathematicians must have visited the town; they left several problems (and prizes for their solutions). The last date figuring in the book is May 31, 1941. Item Number 193 contains a rather cryptic set of numerical results, signed by Steinhaus, dealing with the distribution of the number of matches in a box! After the start of war between Germany and Russia, the city was occupied by German troops that same summer and the inscriptions ceased.
The fate of the Scottish Book during the remaining years of war is not known to me. According to Steinhaus, this document was brought back to the city of Wroclaw by Banach's son, now a physician in Poland. (Many of the surviving mathematicians from Lwow continue their work in Wroclaw. The tradition of the Scottish Book continues. Since 1945, new problems have been formulated and inscribed and a new volume is in progress.)
A general word of explanation may be here in order: I left Poland late in 1935 but, before the war, visited Lwow every summer in 1936, '37, '38, and '39. The last visit was during the summer preceding the outbreak of World War II, and I remember just a few days before I left Poland, around August 15, the conversation with Mazur on the likelihood of war. It seems that in general people were expecting another crisis like that of Munich in the preceding year, but were not prepared for the imminent world war. Mazur, in a discussion concerning such possibilities, suddenly said to me " A world war may break out. What shall we do with the Scottish Book and our joint unpublished papers? You are leaving for the United States shortly -- and presumably will be safe. In case of a bombardment of the city, I shall put all the manuscripts and the Scottish Book into a case which I shall bury in the ground". We even decided upon a location of this secret hiding place; it was to be near the goal post of a football field outside the city. It is not known to me whether anything of the sort really happened. Apparently, the manuscript of the Scottish Book survived in good enough shape to have a typewritten copy made, which Professor Steinhaus sent to me last year.
The existence of such a collection of problems was mentioned on several occasions, during the last 20 years, to mathematical friends in this country. I have received, since, many requests for copies of this document. It was in answer to such oral and written requests that the present translation was made. This spring in an article, "Can We Grow Geniuses in Science?" which appears in Harper's June, 1957 issue, L. L. Whyte alluded to the existence of the Scottish Book. Apparently, the diffusion of this small mystery became somewhat widespread, and this provided another incentive for this translation.
Before deciding to make such an informal distribution, I consulted my teacher and friend (and senior member of the group of authors of the problems), Professor Steinhaus, about the propriety of circulating this collection. With his agreement, I have translated the original text (the original is mostly in Polish) in order to make it available through this private communication.
Even as an author or co-author of some of the problems, I have felt that the only practical and proper thing to do was to translate them verbatim. No explanations or reformulations of the problems have been made.
Many of the problems have since found their solution, some in the form of published papers. (I know of some of my own problems, solutions to which were published in periodicals, among them, e.g. Problem 17, l. Z. Zahorski, Fund. Math. 34 183-245 and Problem 77(a), R. H. Fox, Fund. Math. 34 278-287.)
The work of following the literature in the several fields with which the problems deal would have been prohibitive for me. The time necessary for supplying the definitions or explanations of terms, all very well understood among mathematicians in Lwow, but perhaps not in current use now, would also be considerable. Some of the authors of the problems are no longer living and since one could not treat uniformly all the material, I have decided to make no changes whatsoever.
Perhaps some of the problems will still present an actual interest to mathematicians. At least the collection gives some picture of the interests of a compact mathematical group, an illustration of the mode of their work and thought; and reflects informal features of life in a very vital mathematical centre. I should be grateful if the recipients of this collection were willing to point out errors, supply information about solution to problems, or indicate developments contained in recent literature in topics connected with the subjects discussed in the problems.
It is with great pleasure that I express thanks to Miss Marie Odell for help in editing the manuscript and to Dr. Milton Wing for looking over the translated manuscript . Reference (One book/article)
Article by: S. Ulam
Nota: la seguente indegna traduzione è soltanto una attenta revisione della traduzione fatta da Google al fine di eliminare gli errori più gravi.
Quello che segue è la prefazione a un documento intitolato "The scottish Book" inviato da Stan Ulam da Los Alamos al professor Copson in Edimburgo il 28 gennaio 1958.
PREFAZIONE
L'allegata raccolta di problemi matematici ha la sua origine in un quaderno di appunti che è stato scritto a Lwow (Leopoli), in Polonia nel 1935. Se non ricordo male, è stato S. Banach che ha suggerito di tenere traccia di alcuni dei problemi che occuparono il gruppo di matematici in quella città. La vita matematica era molto intensa a Lwow. Alcuni di noi si riunivano praticamente ogni giorno, informalmente in piccoli gruppi, a tutte le ore del giorno per discutere problemi di comune interesse, e per comunicare gli uni agli altri l'ultimo lavoro e i risultati raggiunti.
A parte le riunioni ufficiali delle sezioni locali della Mathematical Society (che avevano luogo il sabato sera, quasi ogni settimana!), vi erano frequenti discussioni informali in gran parte tenute in uno dei caffè situato vicino all'Università - uno di loro era un caffè casa denominato "Roma" e l'altro "The Scottish Coffee House". Questo spiega il nome della collezione.

The Scottish Coffee House
Un grande quaderno fu acquistato da Banach e lasciato in custodia al gestore dello Scottish Coffee House, che lo teneva in un posto sicuro e, su richiesta, lo portava agli ospiti matematici. Potete vedere una foto dello Scottish Café. Molti dei problemi sono precedenti al 1935. Essi sono stati discussi tra le persone i cui nomi sono scritti nel testo.
La maggior parte dei quesiti proposti dovevano avere una notevole attenzione dedicataalla loro prima di essere inclusi "ufficialmente" "libro". Come il lettore vedrà, questa regola generale non poteva garantire nei confronti di una occasionale domanda alla quale la risposta è stata abbastanza semplice o addirittura banale. In molti casi, i problemi sono stati risolti, immediatamente o entro un breve periodo di tempo, e le risposte sono state scritte, forse un po' di tempo dopo la prima formulazione del problema sotto esame.
Come la maggior parte dei lettori capiranno, la città di Lwow, e con essa lo "Scottish Book", è stato destinato ad avere una storia molto burrascosa nel giro di pochi anni dalla nascita del libro. Poche settimane dopo lo scoppio della Seconda Guerra Mondiale, la città fu occupata dai russi. Da scritti che si trovano alla fine di questa raccolta, si deduce che alcuni matematici russi devono avere visitato la cittàlasciando diversi problemi (e premi per le loro soluzioni). L'ultima data che compare nel libro è il 31 maggio 1941. Il problema n. 193 contiene una serie un po' criptica di risultati numerici, firmata da Steinhaus, che riguarda la distribuzione del numero di cerini in una scatola!
Dopo l'inizio della guerra tra la Germania e la Russia, la città fu occupata da truppe tedesche durante l'estate e le snnotazioni sul quaderno ebbero fine. Il destino del libro scozzese durante i restanti anni di guerra non mi è noto. Secondo Steinhaus, questo documento è stato portato a Breslavia dal figlio di Banach, che ora è un fisico in Polonia. Molti dei superstiti matematici da Lwow continuano il loro lavoro a Wroclaw.
La tradizione dello Scottish Book continua. Dal 1945, i nuovi problemi sono stati formulati e scritti, e un nuovo volume è in corso. Un generale parola di spiegazione può essere qui in ordine: ho lasciato la Polonia tardi, ma nel 1935, prima della guerra, ho visitato Lwow ogni estate nel 1936, '37, '38, e '39.
L'ultima visita è stata durante l'estate precedente lo scoppio della Seconda Guerra Mondiale, e mi ricordo, solo un paio di giorni prima di lasciare la Polonia, circa il 15 agosto, la conversazione con Mazur sulla probabilità di guerra. Sembra che, in generale, le persone si aspettavano un'altra crisi come quella di Monaco di Baviera l'anno precedente, ma non erano preparati per l'imminente guerra mondiale.
Mazur, in una discussione relativa a tali possibilità, improvvisamente mi disse: "Potrebbe scoppiare una guerra mondiale. Che cosa dobbiamo fare con lo Scottish Book e i nostri manoscritti inediti? Presto partirai per gli Stati Uniti e presumibilmente sarai al sicuro. In caso di bombardamento della città, vorrei mettere tutti i manoscritti e lo Scottish Book in una cassa che seppellirò sotto terra". Decidemmo anche sulla posizione di questo nascondiglio segreto, che era vicino a una porta di un campo di calcio al di fuori della città. Non so se ciò è accaduto veramente.
Apparentemente, il manoscritto dello Scottish Book sopravvisse in buona forma sufficiente per avere un copia dattiloscritta, che il professor Steinhaus mi ha inviato l'anno scorso. L'esistenza di una tale raccolta di problemi è stata menzionata in numerose occasioni, nel corso degli ultimi 20 anni, da amici matematici in questo paese. Ho ricevuto, molte richieste di copie di questo documento.
È in risposta a tali richieste orali e scritte che ho scritto la presente traduzione in inglese.
Questa primavera, in un articolo, "Can We Grow Geniuses in Science?" which appears in che appare in Harper's June, 1957, L.L. Whyte accennò all'esistenza dello Scottish Book. Apparentemente, la diffusione di questo piccolo mistero divenne piuttosto diffusa, e ciò ha fornito un ulteriore incentivo per questa traduzione.
Prima di decidere di effettuare tale distribuzione informale, ho consultato il mio maestro e amico (e membro anziano del gruppo di autori dei problemi), il professor Steinhaus, circa la correttezza di far circolare questa raccolta. Con il suo accordo, ho tradotto il testo originale (l'originale è in gran parte in polacco), al fine di renderlo disponibile attraverso questa comunicazione privata.
Anche come autore o co-autore di alcuni dei problemi, ho sentito che l'unica cosa concreta e corretta da fare è stato quello di tradurre letteralmente. Non ho aggiunto spiegazioni né ho fatto riformulazione dei problemi.
Molti dei problemi hanno trovato la loro soluzione, alcuni sotto forma di articoli pubblicati. (So di alcuni dei miei problemi, le cui soluzioni sono state pubblicate in riviste, come ad esempio, Problem 17, l. Z. Zahorski, Fund. Math. 34 183-245 and Problem 77(a), RH Fox, Fund. Math. 34 278-287).
Seguire la letteratura scientifica nei vari settori con i quali affrontare i problemi sarebbe stato proibitivo per me. Aarebbe anche considerevole il tempo necessario per fornire le spiegazioni o definizioni di termini, tutti molto ben compresi tra matematici in Lwow, ma forse non in uso ormai corrente. Alcuni degli autori dei problemi non sono più in vita e poiché non si potrebbe trattare in modo uniforme tutto il materiale, ho deciso di non effettuare modifiche di sorta. Forse alcuni dei problemi presenta ancora un effettivo interesse per i matematici.
Almeno la raccolta dà un'idea degli interessi di un piccolo gruppo di matematica, un esempio del loro lavoro e pensieroe rispecchia le caratteristiche della vita informale in un centro vitale matematica.
Sarei grato se i destinatari di questa collezione saranno disposti a segnalare errori, fornire informazioni circa la soluzione dei problemi, o di indicare gli sviluppi recenti contenuti nella letteratura in argomenti connessi con i temi discussi i problemi.
E' con grande piacere che ringrazio Miss Marie Odell per un aiuto nella scrittura del manoscritto e al dottor Milton Wing per l'attento esame del manoscritto tradotto.
Articolo di: S. Ulam
Nota: Stanislaw Ulam (Leopoli, 13 aprile 1909 – Santa Fe, 13 maggio 1984) è stato un matematico polacco che partecipò al progetto Manhattan e propose il progetto Teller–Ulam per le armi nucleari. Egli inventò la propulsione nucleare ad impulso e sviluppò una serie di strumenti matematici per la teoria dei numeri e degli insiemi, per la teoria ergodica e per la topologia algebrica. (tratto da Wikipedia)
Una versione integrale dello Scottish Book si trova nel sito dedicato a Sefan Banach: http://banach.univ.gda.pl/e-scottish-book.html
Oggi, per motivi legati al mio lavoro (non matematici), stavo consultando la rivista "Le Scienze" dell'agosto 2006. Mi sono imbattuto in questo bellissimo articolo di Dario Bressanini. Lo cito qui di seguito sperando che piaccia a voi quanto è piaciuto a me.
L'influenza del lavoro di un gruppo di matematici polacchi, raccolto in un quaderno che si salvò dalla guerra grazie a un ingegnoso espediente, non è ancora spenta
di Dario Bressanini
Gli anni tra le due guerre mondiali furono un periodo di grande sviluppo per la matematica del XX secolo. Uno dei centri più vivaci era una cittadina polacca, Lwow (che oggi fa parte dell'Ucraina), dove operavano personaggi del calibro di Hugo Steinhaus, Marc Kac, Stanislaw Ulam e soprattutto Stefan Banach, uno dei padri fondatori della moderna analisi funzionale.
Il luogo di lavoro preferito non era, però, l'università, bensì i caffè del quartiere universitario: prima il Caffè Roma e in seguito il Caffè Scozzese, Kawiarnia Szkocka.
Quasi ogni giorno un gruppo di matematici, guidato da Banach, si ritrovava al caffè per passare ore e ore a discutere di matematica. I tavoli di marmo bianco venivano usati per scrivere formule, fare congetture e schizzare dimostrazioni. A volte qualcuno poneva un problema, e tutti restavano a lungo in silenzio, fissando il vuoto e meditando sulla questione tra lo stupore degli altri avventori.
Nel 1935 Banach portò al Caffè Scozzese un grosso quaderno da usare per ricopiare i problemi più interessanti sorti nelle discussioni, assieme ai risultati e alle dimostrazioni più notevoli. Il libro fu dato in custodia al gestore del locale: su richiesta del gruppo, veniva portato al tavolo da una cameriera e poi riconsegnato al proprietario del Caffè.
Alcuni problemi venivano risolti all'istante, mentre per la soluzione di altri si metteva in palio un premio. I premi, annotati sul quaderno, variavano da "un paio di birre piccole" a una "fonduta alla ginevrina", ma ce n'erano anche di più insoliti, per esempio "100 grammi di caviale" o "un'oca viva".
Nel corso degli anni vari famosi matematici, come Henri Lebesgue, John von Neumann e Waclaw Sierpinski, visitarono il gruppo di Lwow, e qualcuno dei problemi che proposero fu trascritto nel quaderno.
Il volume, una raccolta di 193 problemi, annotati dal 1935 al 1941, sarebbe poi divenuto famoso come "il libro scozzese", e avrebbe avuto una grande influenza nello sviluppo di molti settori della matematica. Il 1° ottobre 1939 le truppe sovietiche occuparono Lwow; dai problemi riportati nel quaderno sembra che alcuni matematici russi, come Sobolev, passarono a visitare Banach e colleghi. L'ultimo problema è datato 31 maggio 1941.
Di lì a pochi giorni le truppe naziste sarebbero entrate in città e, per ordine di Himmler, avrebbero assassinato decine di studiosi, scrittori e rappresentati della cultura. Banach, nonostante i suoi buoni rapporti con i sovietici, si salvò: morì di cancro nel 1945. Il libro però gli sopravvisse. Prima dell'inizio della guerra, infatti, Ulam e il collega Mazur si erano accordati sul da farsi per evitarne la distruzione o la perdita: in caso di bombardamento, Mazur doveva metterlo in una scatola e seppellirlo vicino alla rete del campo da calcio appena fuori città.
Dopo la guerra, il libro fu ritrovato dal figlio di Banach, che lo diede a Steinhaus il quale lo spedì a Ulam, trasferitosi a Los Alamos, negli Stati Uniti.
La fama del libro e dei problemi in esso contenuti è cresciuta col tempo. Nel 1957 Ulam ne fece delle copie per rispondere alle richieste sempre maggiori provenienti da matematici di tutto il mondo, fino a quando, nel 1977, ne fu preparata una prima edizione libraria.
A tutt'oggi è ancora irrisolto quasi un quarto dei problemi che vi sono esposti e l'influenza sullo sviluppo della matematica di quel quaderno scritto a mano tra tè, birre e caffè non si è ancora spenta.
Data creazione: dicembre 2008
Ultimo aggiornamento: dicembre 2008
xhtml 1.1
Sito Web realizzato da Gianfranco Bo