[HOME - BASE Cinque -
Appunti di Matematica ricreativa]
Appunti scolastici in forma
provvisoria e in continuo divenire.
Problemi additivi di base
Sei problemi elementari che stanno alla base di tutti i
problemi complessi
Definizione
Per "problema additivo di base" intendo un problema aritmetico che
si risolve con una sola operazione, che può essere:
una addizione
una sottrazione
Ne esistono sei tipi fondamentali, ciascuno dei quali può
presentarsi in tre modi diversi.
I tre aspetti dell'addizione
Partiamo da una semplicissima addizione:
a + b = c
In essa compaioni 3 termini: i due addendi e il totale.
L'addizione può essere scritta in tre modi diversi, che ci permettono di
calcolare un termine conoscendo gli altri due:
c = b + a
b = c - a
a = c - b
In altre parole, se poniamo come incognita uno dei tre
termini possiamo ottenere 3 diverse equazioni:
a + [n] = c
[n] + b = c
a + b = [n]
Ogni volta che si pensa ad una addizione è importante avere
ben presenti (attivare) questi tre punti di vista.
Il significato dei numeri in un contesto additivo
Che cosa possono rappresentare i dati numerici in un problema di tipo
additivo?
Una misura statica
Marco è alto 145 cm
Luigi ha 35 Euro
I numeri 145 e 35 rappresentano misure o dati statici.
Una trasformazione di misure
Marco ha perso 3 figurine
Marco è cresciuto di 5 cm
I numeri 3 e 5 rappresentano variazioni in aumento o
diminuzione. Ad esempio, non sappiamo quanto è alto Marco, ma soltanto
di quanto è cresciuto, di quanto si è trasformata la sua altezza.
E' importante notare che queste trasformazioni sono di tipo additivo e non,
ad esempio, moltiplicativo. Cioè non sono del tipo: raddoppia, triplica,
dimezza, etc.
Una relazione fra misure
Marco pesa 5 kg più di Maria.
Marco ha 3 euro meno di Giovanni.
I numeri 3 e 5 rappresentano una relazione che c'è fra due
misure. Ad esempio, non sappiamo quanti Euro hanno Marco e Giovanni ma
soltanto quanti ne ha Marco meno di Giovanni.
Anche in questo caso è importante notare che queste relazioni sono di tipo
additivo, cioè, in pratica, indicano una differenza e non un
rapporto.
I sei problemi di base
Ciascun problema additivo può presentarsi in tre modi diversi, corrispondenti
ai tre aspetti dell'addizione.
1. Composizione di misure statiche
- Carlo ha 35 Euro, Roberta ne ha 50, quanto hanno insieme Carlo e
Roberta?
Il calcolo da eseguire é:..............................
- Due libri sono costituiti complessivamente da 356 fogli. Il primo
volume è formato da 134 fogli. Da quanti fogli è costituito il secondo
volume?
Il calcolo da eseguire é:..............................
- Il babbo ha comprato arance e mele per un peso totale di 5 kg. Sapendo
che le arance pesano 3 kg, quanto pesano le mele?
Il calcolo da eseguire é:..............................
2. Trasformazione di una misura
- Marco aveva 12 Euro, poi ne ha regalato 5 a Roberta. Quanti Euro ha
Marco adesso?
Il calcolo da eseguire é:..............................
- Giovanni, l'anno scorso era alto 130 cm, ora è alto 142 cm. Di quanti
centimetri è cresciuto?
Il calcolo da eseguire é:..............................
- Diego, dopo aver speso 3 Euro è rimasto con 5 Euro. Quanti Euro aveva
all'inizio?
Il calcolo da eseguire é:..............................
3. Confronto fra due misure
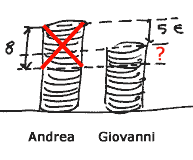
- Marco ha 7 Euro. Roberta ha 8 Euro più di Marco. Quanto ha Roberta?
Il calcolo da eseguire é:..............................
- Andrea pesa 43 kg, Guglielmo pesa 38 kg. Quanti chilogrammi pesa Andrea
più di Guglielmo
Il calcolo da eseguire é:..............................
- Marco ha 7 libri meno di Roberta. Roberta ha 36 libri. Quanti libri ha
Marco?
Il calcolo da eseguire é:..............................
4. Composizione di trasformazioni
5. Trasformazione di una relazione
6. Composizione di relazioni
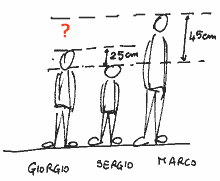
- Giorgio è 25 cm più alto di Sergio. Sergio è 45 cm più basso di Marco.
Marco è più basso o più alto di Giorgio? Di quanti centimetri
esattamente?
Il calcolo da eseguire é:..............................
Suggerimento: anche in questo caso, un disegno può aiutare a
risolvere il problema.
- Maria, Giuliana e Roberta fanno una gara di corsa. Vince chi corre i
cento metri nel minor tempo. Maria impiega 9 secondi meno di Roberta.
Giuliana impiega 6 secondi più di Roberta. Chi ha vinto la gara? Chi è
arrivato ultimo? Quanti secondi di differenza ci sono esattamente fra
Maria e Giuliana?
Il calcolo da eseguire é:..............................
Suggerimento: fai un disegno delle tre ragazze in ordine di
arrivo.
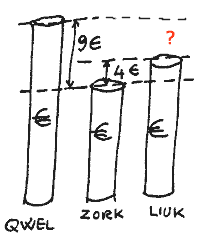
- Uno zork costa 4 Euro meno di un liuk. Un qwel costa 9 Euro più di uno
zork. Costa di più un liuk o un qwel? Di quanti euro esattamente?
Il calcolo da eseguire é:..............................
Osserva il disegno.
I problemi additivi complessi
I problemi additivi complessi in genere sono una combinazione di problemi
più semplici e si risolvono con due o più addizioni o sottrazioni.
Prima di risolvere un problema è bene avere un piano d'azione e spesso è
utile fare un disegno che illustri la situazione. Ecco un esempio:
- Marco deve percorrere tre tratti di strada. Il primo tratto è lungo 12
km e ciascuno dei successivi è lungo 4 km più del precedente. Quanto è
lungo complessivamente il tratto che Marco deve percorrere?
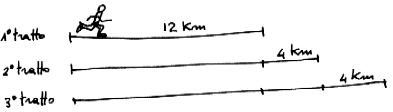
1° tratto: 12 km;
2° tratto: 12 + 4 =16 km;
3° tratto: 16 + 4 = 20 km;
Lunghezza complessiva: 12 + 16 + 20 = 48 km
Data creazione: dicembre 2003
Ultimo aggiornamento: aprile 2006
Sito Web realizzato da Gianfranco Bo