| Una piccola
premessa. Il mondo
additivo di cui parlo è quello dei numeri naturali,
delle addizioni e delle sottrazioni.
Come sono definiti i numeri
naturali in matematica?
Come sono definite le operazioni di addizione
e sottrazione?
Quali sono le loro proprietà
fondamentali?
A me piace l'impostazione di Giuseppe
Peano.
Egli definisce l'addizione ricorsivamente
(o induttivamente) e definisce la sottrazione come
operazione inversa dell'addizione.
Significato dei simboli usati:
N0
significa "numero", cioè è il
nome comune di 1, 2, 3, ...
0 significa "zero"
' significa "successivo".
Se a è un numero, a' è il
successivo di a
=> significa "implica
logicamente"
<> significa "diverso
da"
e significa "appartiene",
è il simbolo che indica l'appartenenza di un
elemento ad un insieme o classe
Gli assiomi dell'aritmetica
secondo Giuseppe Peano
N0, 0, '
indicano le tre idee primitive per mezzo delle quali
si possono definire tutte le altre idee
dell'aritmetica.
Possiamo definire matematicamente
queste tre idee?
Lo possiamo fare implicitamente,
attraverso un sistema di assiomi.

0. N0
e Cls (N0 è una
classe, un insieme)
1. 0 e N0
(Zero è un numero)
2. a
e
N0
=> a'
e N0
(Se a è un numero, allora il suo successivo
è un numero)
3. Principio di induzione:
a) se una condizione o proposizione P è soddisfatta
per n=0;
e se:
b) il fatto che sia soddisfatta per n implica che è
soddisfatta per n+1
allora tale proprietà è soddisfatta per ogni n.
4. a,b
e
N0
, a' = b'
=> a = b
(Se due numeri hanno successivi uguali, allora
sono uguali)
5. a
e
N0
=> a'
<> 0 (0 non è il successivo di alcun
numero)
Definizione di addizione
1. a e N0
=> a+0=a
2. a,b
e
N0
=> a+b'
= (a+b)'
Come si possono esprimere, a
parole, le espressioni 1. e 2.?
1. Se a è un numero, allora a+0
vale a.
2. Se a e b sono numeri, allora la
somma di a con il successivo di b
è uguale al successivo della somma di a con
b. Per "somma" si intende il
risultato dell'addizione.
L'addizione gode delle proprietà associativa
e commutativa.
Associativa
a,b,c
e
N0
=> (a+b)+c
= (a+b)+c
Questa proprietà deve essere dimostrata.
Per definizione: a+b+c = (a+b)+c
Commutativa
a,b
e
N0
=> a+b = b+a
Questa proprietà deve essere dimostrata.
Definizione di sottrazione
Scrivo la definizione "a parole".
Se a è un numero e b è un numero
maggore o uguale di a, allora b-a
indica quel numero x tale che x+a
vale b.
Un'altra possibile
assiomatizzazione dell'aritmetica
Ecco un'altra assiomatizzazione dell'aritmetica
espressa in una notazione più "moderna"
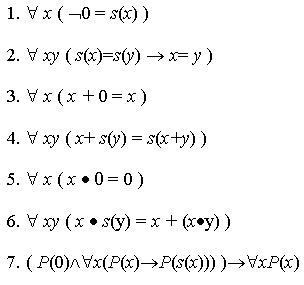
Da notare che gli
assiomi 3, 4 definiscono l'addizione, mentre gli
assiomi 5, 6 definiscono la moltiplicazione in N0.
L'assioma 7 è in realtà uno schema di
assiomi che esprime il principio di
induzione. Si chiama "schema di assiomi"
perché rappresenta non uno ma infiniti assiomi:
infatti al posto di P possono essere sostituite
infinite proposizioni.
|