[HOME - BASE Cinque -
Appunti di Matematica ricreativa]
Appunti scolastici in forma
provvisoria e in continuo divenire.
Il mondo moltiplicativo
Teoria minima
| Una piccola premessa.
Il mondo moltiplicativo di cui parlo è quello dei
numeri naturali, delle moltiplicazioni e delle divisioni.
Come sono definiti i numeri naturali in
matematica?
Come sono definite le operazioni di moltiplicazione e
divisione?
Quali sono le loro proprietà fondamentali?
A me piace l'impostazione di Giuseppe
Peano.
Egli definisce la moltiplicazione ricorsivamente (o
induttivamente), utilizzando anche l'addizione, e definisce la
divisione come operazione inversa della moltiplicazione.
Significato dei simboli usati:
N0 significa "numero", cioè è il
nome comune di 1, 2, 3, ...
0 significa "zero"
' significa "successivo". Se a è un numero,
a' è il successivo di a
=> significa "implica logicamente"
<> significa "diverso da"
e
significa "appartiene", è il simbolo che indica
l'appartenenza di un elemento ad un insieme o classe
Gli assiomi dell'aritmetica secondo Giuseppe
Peano
N0, 0, ' indicano le tre idee primitive
per mezzo delle quali si possono definire tutte le altre idee
dell'aritmetica.
Possiamo definire matematicamente queste tre idee?
Lo possiamo fare implicitamente, attraverso un sistema di
assiomi.

0. N0 e Cls
(N0 è una classe, un insieme)
1. 0 e N0 (Zero è un
numero)
2. a e N0 =>
a' e N0 (Se a è un numero, allora
il suo successivo è un numero)
3. Principio di induzione:
a) se una condizione o proposizione P è soddisfatta per n=0;
e se:
b) il fatto che sia soddisfatta per n implica che è soddisfatta per
n+1
allora tale proprietà è soddisfatta per ogni n.
4. a,b
e N0 , a' =
b' => a =
b (Se due numeri hanno successivi
uguali, allora sono uguali)
5. a e N0 =>
a' <> 0 (0 non è il successivo di
alcun numero)
Definizione di moltiplicazione
1. a e N0 =>
ax0=0
2. a,b e N0 =>
axb' =
(axb)+a
Come si possono esprimere, a parole, le espressioni
1. e 2.?
1. Se a è un numero, allora ax0 vale 0.
2. Se a e b sono numeri, allora il prodotto di
a per il successivo di b è uguale alla somma del
prodotto di a per b con a. Per "prodotto"
si intende il risultato della moltiplicazione.
La moltiplicazione gode delle proprietà
distributiva rispetto all'addizione, associativa,
commutativa.
Distributiva (x,+)
a,b,c e N0 =>
ax(b+c)
=
axb+axc
Questa proprietà deve essere dimostrata.
Associativa
a,b,c e N0 =>
(axb)xc
=
(axb)xc
Questa proprietà deve essere dimostrata.
Per definizione: axbxc =
(axb)xc
Commutativa
a,b e N0 =>
axb =
bxa
Questa proprietà deve essere dimostrata.
Definizione di divisione
Scrivo la definizione "a parole".
Se a è un numero e b è un numero diverso da zero,
allora b/a indica quel numero n tale che
nxa vale b.
Un'altra possibile assiomatizzazione
dell'aritmetica
Ecco un'altra assiomatizzazione dell'aritmetica espressa in una
notazione più "moderna"
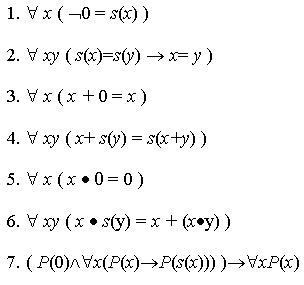
Da notare che gli assiomi 3, 4
definiscono l'addizione, mentre gli assiomi 5, 6 definiscono la
moltiplicazione in N0.
L'assioma 7 è in realtà uno schema di assiomi che esprime il
principio di induzione. Si chiama "schema di assiomi" perché
rappresenta non uno ma infiniti assiomi: infatti al posto di P
possono essere sostituite infinite proposizioni.
|
1. Moltiplicazione
Definizione
Moltiplicare due numeri naturali significa addizionare tanti addendi
uguali al primo numero quante sono le unità del secondo numero.
I simboli della moltiplicazione sono: x,
·(per)
5 x 4 = 5 + 5 + 5 + 5 = 20
5 x 4 = 20 oppure 5 4 = 20
a x b = a + a + a + ... + a (ripetuto b volte) =
c
Quando si utilizzano le lettere per rappresentare i numeri,
il segno di moltiplicazione può essere omesso.
a x b = c oppure a · b = c oppure
ab = c
I due termini della moltiplicazione si chiamano
fattori, o rispettivamente moltiplicando e
moltiplicatore, mentre il risultato si chiama
prodotto.

21
|
x
|
8
|
=
|
168
|
moltiplicando
|
|
moltiplicatore
|
|
prodotto
|
Il prodotto di tre o più numeri naturali, dati in un
certo ordine, è il numero che si ottiene moltiplicando il primo per il
secondo e il prodotto ottenuto per il terzo numero e così via.
3 x 5 x 6 x 10 = 15 x 6 x 10 = 90 x 10 = 900
2. Proprietà della moltiplicazione
Proprietà commutativa.
Il prodotto non cambia invertendo l'ordine dei fattori.
3 x 2 = 2 x 3
a x b = b x a
Proprietà associativa.
Il prodotto di tre o più fattori non cambia se a due o più di essi si
sostituisce il loro prodotto.
3 x 2 x 5 = (3 x 2) x 5 = 6 x 5 = 30
3 x 2 x 5 = 3 x (2 x 5) = 3 x 10 = 30
a x b x c = (a x b) x c = a x (b x c)
Proprietà dissociativa.
Il prodotto di due o più fattori non cambia se ad uno dei fattori si
sostituiscono due o più fattori, il cui prodotto sia uguale al fattore
sostituito.
6 x 5 = 3 x 2 x 5
(a x b) x c = a x b x c
Proprietà distributiva della moltiplicazione rispetto
all'addizione.
Per moltiplicare un'addizione per un numero, si può moltiplicare ciascun
addendo per quel numero e addizionare poi i prodotti così ottenuti.
(3 + 2) x 5 = 3 x 5 + 2 x 5
(a + b) x c = a x c + b x c
Proprietà distributiva della moltiplicazione rispetto
alla sottrazione.
Per moltiplicare una sottrazione per un numero, si possono moltiplicare il
minuendo ed il sottraendo per quel numero ed eseguire poi la sottrazione fra
i prodotti così ottenuti.
(3 - 2) x 5 = 3 x 5 - 2 x 5
(a - b) x c = a x c - b x c
Legge di annullamento del prodotto.
Il prodotto di più fattori è uguale a zero se almeno uno di essi è uguale a
zero e viceversa.
2 x 3 x 0 x 5 x 7 = 0
a x b x 0 x c x d = 0
3. Divisione
Definizione
Dividere un numero naturale per un secondo numero naturale diverso da
zero significa determinare un terzo numero naturale che moltiplicato per il
secondo numero dia per risultato il primo numero.
Il simbolo della divisione è:
15 : 3 = 5 perché 5 x 3 = 15
a : b = c; c x b = a
I termini della divisione si chiamano rispettivamente
dividendo e divisore, il risultato si chiama
quoziente.
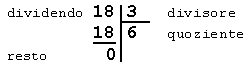
18
|
:
|
3
|
=
|
6
|
| dividendo |
|
divisore |
|
quoziente |
Quoziente approssimato e resto
Quando la divisione non è possibile perché non esiste un numero naturale
che moltiplicato per il divisore dia per risultato il dividendo si ha una
divisione con quoziente approssimato e resto.
Il quoziente approssimato è il più grande numero
naturale che moltiplicato per il divisore dà come risultato un numero che non
supera il dividendo.
38 : 5 = 7 perché 7 x 5 = 35 che è il multiplo di 5 più
vicino a 38 per difetto
Il resto è la differenza fra il dividendo e il
prodotto del divisore per il quoziente.
38 : 5 = 7 con resto = 3, perché
38 - (7 x 5) = 38 - 35 = 3
Si può anche dire:
quoziente x divisore + resto = dividendo
a : b = q, resto = r perché b x q + r = a

25
|
:
|
7
|
=
|
3
|
4
|
| dividendo |
|
divisore |
|
quoziente |
resto |
3
|
x
|
7
|
+
|
4
|
=
|
25
|
quoziente
|
|
divisore
|
|
resto
|
|
dividendo
|
La divisione n : 0
La divisione di un numero diverso da zero per zero è impossibile, cioè
il risultato non esiste.
7 : 0 = impossibile, perché non esiste nessun numero che moltiplicato per 0
dia 7
n : 0 = x (impossibile)
Infatti non esiste nessun numero che moltiplicato per 0 dia n, diverso da
0.
La divisione 0 : 0
La divisione di zero per zero è indeterminata, cioè il risultato
può essere qualunque numero.
0 : 0 = x (indeterminata)
Infatti qualunque numero moltiplicato per 0 (divisore) dà 0
(dividendo).
4. Proprietà della divisione
Proprietà invariantiva.
Moltiplicando o dividendo i due termini di una divisione per uno stesso
numero diverso da 0, il quoziente non cambia e il resto risulta moltiplicato
per quello stesso numero.
20 : 4 = 5
(20 x 3) : (4 x 3) = 60 : 12 = 5
(20 : 2) : (4 : 2) = 10 : 2 = 5
a : b = c
(a x m) : (b x m) = c (con m 0)
(a : n) : (b : n) = c (con n 0)
Proprietà distributiva della divisione rispetto
all'addizione.
Per dividere un'addizione per un numero (purché tutti i termini siano
divisibili per quel numero) si può dividere ciascun addendo per quel numero e
addizionare i quozienti ottenuti.
(36 + 20) : 4 = 36 : 4 + 20 : 4 = 9 + 5 = 14
(a + b) : c = a : c + b : c
Proprietà distributiva della divisione rispetto alla
sottrazione.
Per dividere una sottrazione per un numero (purché tutti i termini siano
divisibili per quel numero) si possono dividere il minuendo e il sottraendo
per quel numero e sottrarre i quozienti ottenuti.
(45 - 35) : 5 = 45 : 5 -35 : 5 = 9 - 7 = 2
(a - b) : c = a : c - b : c
5. I numeri 0 e 1 nella moltiplicazione e nella divisione
| Moltiplicazione
a x 0 = 0
0 x a = 0
a x 1 = a
1 x a = a
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
a x a = a2, il quadrato di a
|
Divisione
a : 0 = impossibile, cioè il risultato non
esiste
0 : a = 0
a : 1 = a
1 : a = il risultato non è in N, tranne nel caso a
= 1
0 : 0 = indeterminata, cioè il risultato può essere
qualsiasi numero
0 : 1 = 0
1 : 0 = impossibile
1 : 1 = 1
a : a = 1
|
6. Cenno ai numeri decimali (Razionali)
7. La media aritmetica
8. Progressioni aritmetiche
9. Progressioni geometriche
Dicembre 2003
Sito Web realizzato da Gianfranco Bo