[BASE Cinque - Appunti di Matematica ricreativa]

Foto di gruppo e altri problemi combinatori di Shakuntala Devi

1. Foto di gruppo

I miei amici Asha, Neesha, Vijay, Parveen e Seema e io stessa (Shakuntala) abbiamo deciso di farci una foto di gruppo nello studio.

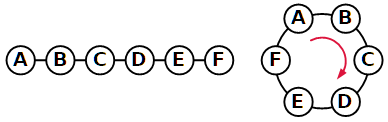
Abbiamo deciso di sederci in fila uno accanto all'altro.

In quante disposizioni diverse avremmo potuto sederci?

Più tardi siamo andati al ristorante. Il cameriere ci ha condotto a un tavolo rotondo.

In quanti modi diversi avremmo potuto sederci attorno al tavolo?

---

Note.

• Ho fatto una breve ricerca per individuare il genere dei nomi indiani delle persone: Vijay è maschile, gli altri sono femminili.
  Se avete informazioni più precise, vi prego di farmelo sapere.
• Questo problema aiuta a riflettere sulla differenza tra permutazioni lineari e permutazioni cicliche.
• Si può semplificare partendo dal caso di 3 persone invece di 6.

2. Bingo!

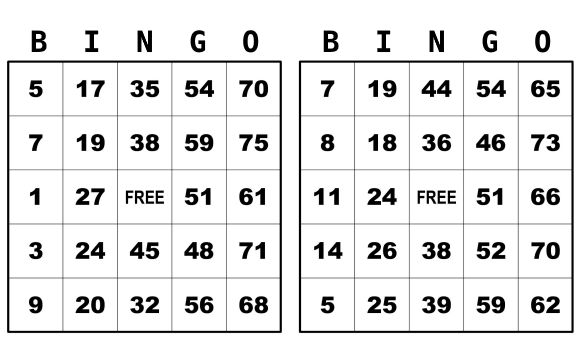
Giocando a Bingo ho notato una cosa molto interessante: ci sono diverse cartelle del Bingo tali che nessuna coppia di esse ha lo stesso insieme di numeri in due righe o in due colonne corrispondenti.

Il centro naturalmente è una casella vuota.

Nella figura ci sono due esempi.

Quante di queste cartelle sono possibili?

---

Nota.

I numeri nelle cartelle del Bingo sono scritti in base alle regole seguenti:

1. Le cartelle hanno cinque colonne di cinque quadrati ciascuna.
2. Ogni quadrato contiene un numero casuale compreso tra 1 e 75 (eccetto il quadrato centrale, che è designato come spazio "LIBERO-FREE").
3. Procedendo da destra verso sinistra, le colonne sono etichettate come
   "B" numeri casuali nell'intervallo [1-15],
   "I" numeri casuali nell'intervallo [16-30],
   "N" numeri casuali nell'intervallo [31-45],
   "G" numeri casuali nell'intervallo [46-60],
   "O" numeri casuali nell'intervallo [61-75].

3. Due pedine sulla scacchiera

Una scacchiera ha 64 caselle.

a) In quanti modi distinti si possono mettere due pedine diverse (una bianca e una nera) sulla scacchiera?

b) E se invece le pedine fossero uguali?

---

Problemi tratti e rielaborati da: Shakuntala Devi, More Puzzles to Puzzle You, 1985, 2000.

I problemi originali hanno un po' più narrazione.

Risposte & riflessioni

1. Foto di gruppo

Permutazioni lineari: 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720

Permutazioni cicliche: 6! : 6 = (6 - 1)! = 120

Basta osservare che a ogni disposizione di 6 persone intorno a un tavolo corrispondono 6 distinte permutazioni lineari.

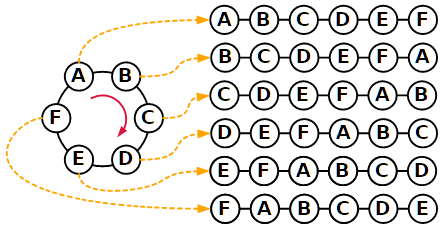
In generale, se le persone sono n, a ogni disposizione di n persone intorno a un tavolo corrispondono n distinte permutazioni lineari.

• Permutazioni di n oggetti distinti: P(n)= n!
• Permutazioni cicliche di n oggetti distinti: P-cicliche(n)= (n-1)!

2. Bingo!

Shakuntala considera la colonna centrale, N, che è la più restrittiva perché ha 4 possibilità invece di 5.

I quattro numeri devono essere scelti dall'insieme {31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45}

In quanti modi si possono scegliere 4 oggetti su 15?
Sono le combinazioni senza ripetizione di 15 oggetti a gruppi di 4 il cui numero è:

---

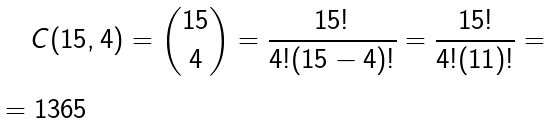
La formula per calcolare il numero delle combinazioni senza ripetizione di n oggetti a gruppi di k è:

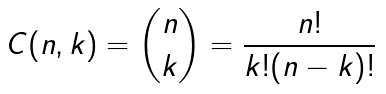
3. Due pedine sulla scacchiera

a) La prima pedina ha 64 posizioni possibili. Per ognuna di esse, la seconda pedina ha le rimanenti 63 posizioni libere.

Pedine diverse: 64 × 63 = 4032

b) Pedine uguali:  4032 : 2 = 2016 (i modi dimezzano)

.

.

---

Pace e bene a tutti.

GfBo

Data creazione: giugno 2021

Ultimo aggiornamento: giugno 2021

html5

Sito Web realizzato da Gianfranco Bo