[BASE Cinque - Appunti di Matematica ricreativa]
o più semplicemente: anello e manette
Ringrazio di cuore Leandro, Pietro Vitelli e Giobimbo, per i contributi a questo problema sul Forum di BASE Cinque.
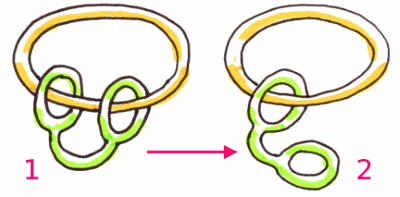
La figura rappresenta due forme intrecciate.
Immaginatele come due palloncini di gomma infinitamente elastica. Considerate solo la loro superficie.
Per la precisione sono superfici di tori, uno di genere 1 (un buco) e l'altro di genere 2 (due buchi).

Come si fa per trasformarle l'una nell'altra con una deformazione continua, senza fare né tagli né saldature?
Disegnate le varie fasi.
Nota storica. Come segnalato da Giobimbo nelle risposte, questo
problema è stato proposto da Martin Gardner sulla rivista Le Scienze n. 140,
pubblicato nella versione italiana del 1980.
Gardner lo definisce "Paradosso toroidale" e lo attribuisce a Herbert Taylor .
"Sono grato a Herbert Taylor per aver scoperto e avermi inviato questo sconcertante problema."
(se è quello che penso io, era molto giovane nel 1980, perché si è laureato
nel 1981 alla University of Southern California, il suo advisor era
Solomon Golomb)
(postato da Leandro al Forum)
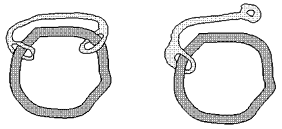
Le due figure qui sopra indicano due insiemi A, B in R , ciascuno costruito
utilizzando due corpi, "anello" e "manette".
I due corpi (tridimensionali e "pieni") sono realizzati con un materiale
illimitatamente elastico.
L'insieme B può essere ottenuto dall'insieme A mediante sole deformazioni
elastiche (cioè senza tagli, fori o incollature).
Indicare come, disegnando le varie fasi in sequenza. (18 punti)
(tratto dalle gare matematiche "Federigo Enriques", Dip. Mat. Uni. Milano, 16
gennaio 1997).
Attenzione. In questa versione i due oggetti sono "pieni", mentre nella versione di Taylor-Gardner si considera solo la loro superficie, come se fossero palloncini gonfiati.
(postato da Pietro Vitelli al Forum)
Non saprei come risolvere il problema (precedente), però colgo l'argomento per postare un problema molto simile al tuo presente su uno dei volumi di Martin Gardner. Sul volume è riportata anche la soluzione che però non ho mai capito. Ecco il problema e la soluzione presente sul volume:

Si tratta di separare i due "oggetti chiusi" senza tagliarli. La soluzione
riportata da Gardner è la seguente: "Le curve possono essere separate
facendo passare la curva ritorta attraverso se stessa nel punto A."
Come si fa?
Ecco una sintesi di due soluzioni.
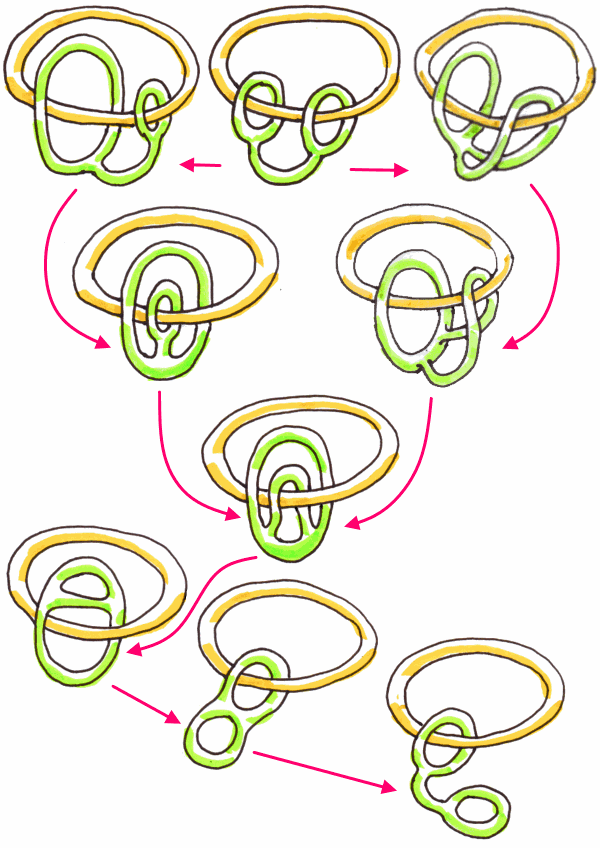
Il problema è equivalente a quello precedente.
Le illuminanti considerazioni di Giobimbo
Premesso che anche il problema delle manette viene da Martin Gardner, vedi la
sua rubrica nei numeri 140 e 141 della rivista "Le Scienze", bisogna dire che a
causare la perplessità di Admin è il fatto che nell'edizione italiana
manca la parola "taglio". Difatti, la didascalia originale, tratta dal
libro Hexaflexagons and Other Mathematical Diversions recita:
"Interlocked curves that can be separated without passing one through an opening in the other. The curves at the top may be separated by passing the twisted curve through a cut in itself at A, then rejoining the ends."
Siccome l'inglese Pietro lo sa, non sto a ritradurre in italiano, ma piuttosto vorrei fare un riassunto a beneficio degli interessati che non conoscono il problema.
Gardner parla di anelli agganciati tra loro, tipo gli anelli di una catena, che per essere liberati richiedono l'apertura di un anello e il passaggio dell'altro attraverso questa apertura. Ma, aggiunge poi, due curve chiuse possono essere agganciate in modo che la loro liberazione non richieda tale operazione, e qui cita l'esempio della figura. Nella figura, scrive, bisogna sempre aprire una curva ma a passare attraverso l'apertura stavolta non è l'altra curva ma la stessa curva in cui si è fatto il taglio. Nel punto A si incrociano due pezzi della curva intrecciata, uno passa sopra l'altro; dopo l'operazione di taglio e saldatura i due pezzi passano uno sotto l'altro e le due curve sono ora libere.
Di mio faccio notare che, a compensazione del comportamento anomalo delle due curve, se tagliamo una delle due e facciamo passare l'altra nell'apertura, dopo la saldatura del taglio le curve stavolta sono ancora agganciate.
Data creazione: dicembre 2006
Ultimo aggiornamento: giugno 2019
xhtml 1.1
Sito Web realizzato da Gianfranco Bo