[BASE Cinque - Appunti di Matematica ricreativa]
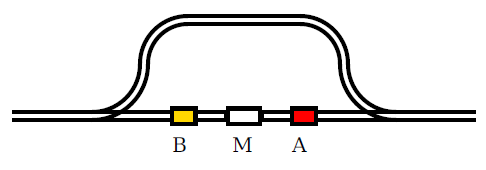
Riuscirà la locomotiva a scambiare i vagoni?
Qui sotto vedete un semplice circuito ferroviario.
Il compito è quello di scambiare il vagone A con il vagone B, lasciando tutto il resto immutato.
In pratica, dopo gli opportuni trasferimenti, si dovrebbe avere una situazione come quella seguente.
Stesso esercizio su questo circuito.
Stesso esercizio su questo circuito.
Il primo caso è un classico, abbastanza facile da risolvere.
Il terzo caso è più difficile, forse impossibile...?
In una stazione ferroviaria di una linea a binario unico, il binario si sdoppia in due tratti, a-d-b e a-c-b per permettere il passaggio di due treni come mostrato in fig. 7.
Su ciascuno dei due tratti c'è spazio per 20 vagoni.
In questa stazione, si incontrano due treni, A e B con 24 vagoni ciascuno.
Come possono passare e proseguire la propria corsa?
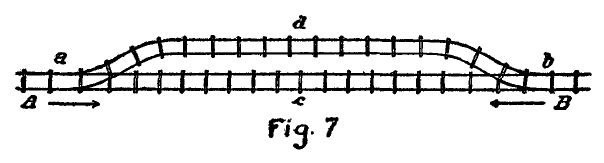
At a railroad station a single-track line, a-b, has a siding, d, as shown in Fig. 7. On each of the two tracks there is space for 20 cars. At this station, two trains, A and B meet with 24 cars each. How can they pass each other?
Joseph Degrazia, Math tricks, brain twisters, and puzzles, 1883 (pubblicato anche col titolo: Math is fun).
Nella figura qui sotto è disegnato un circuito ferroviario formato da un binario principale L, dal quale si staccano due derivazioni che vanno a unirsi in un breve tratto rettilineo che può contenere un vagone ma non la motrice.
Nei due tratti I e II si trovano rispettivamente i vagoni A (rosso) e B (giallo).
Sul binario principale si trova la motrice L (blu).
Come può fare l'autista per scambiare di posto ai due vagoni?
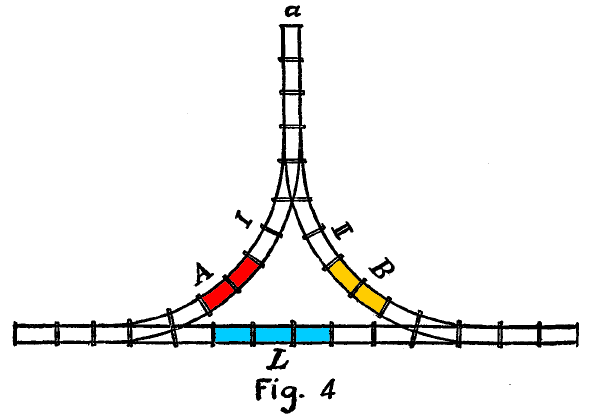
From the main track, two shunting tracks, I and II, branch off, both leading to a short track, a, which is just long enough to receive one car, though not an engine (Fig 4.)
Car A stands on I, Car B on II, while the donkey engine, L, stands ready on M. Now, how can L shunt A on to II and B on to I without cutting itself off from access to the main track?
Joseph Degrazia, Math tricks, brain twisters, and puzzles, 1883 (pubblicato anche col titolo: Math is fun).
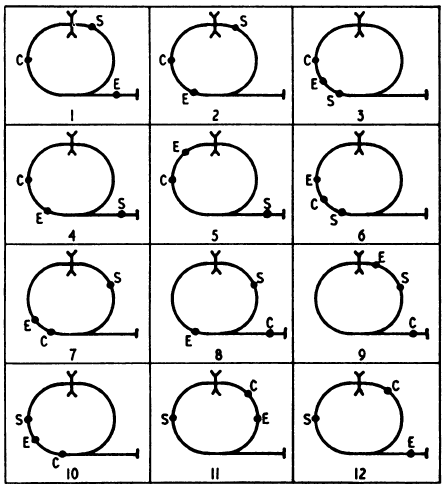
Anche in questo caso bisogna scambiare le posizioni dei vagoni C e S usando la motrice E.
C'è una piccola difficoltà: solo la motrice può passare sotto il ponte, i vagoni no.
Alla fine la motrice si deve trovare al posto iniziale.
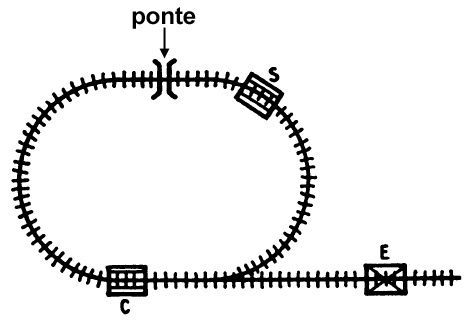
Here we show a small portion of the British Railways shunting yards at East Wapping (you do appreciate we cannot possibly show you all of it). Only the engine can pass under the bridge, and the problem is to reverse the positions of the truck containing sheep and that containing cattle, returning the engine to its present position.
P. M. H. Kendall and G. M. Thomas, Mathematical Puzzles for the Connoisseur, Thomas Y. Crowell Company New York, 1971.



Data creazione: gennaio 2011
Ultimo aggiornamento: gennaio 2011
xhtml 1.1
Sito Web realizzato da Gianfranco Bo