[HOME - BASE Cinque - Appunti di
Matematica ricreativa]
Il problema delle cinque camere
Il problema delle
cinque camere (A)
La figura qui sotto rappresenta la pianta di un appartamento.
Ricopiatela su un foglio di carta.

Come vedete, ci sono 5 camere, ciascuna delle quali
comunica con le altre adiacenti e con l'esterno. In totale ci sono
ben 15 porte.
|
Il problema chiede di
tracciare una linea continua tale che:
1) passi attraverso tutte le porte;
2) passi attraverso ciascuna porta esattamente una volta;
3) non abbia incroci.
L'esempio qui sotto serve soltanto a dare un'idea di
come si dovrebbe procedere ma non è una soluzione corretta.

|
Vi è sembrato facile? Bene, allora spostiamo un muro e
apriamo una nuova porta.
Il problema delle cinque camere (B)
Siete capaci di risolvere il problema in questo caso?

Il problema delle sei camere (C)
Siete capaci di risolvere il problema in questo caso?

Basta fare un po' di prove per rendersi conto dei fatti
seguenti.
|
Caso A

In questo caso il problema si può risolvere
soltanto partendo da un punto interno alla camera più grande o da un
punto esterno all'appartamento
|
Caso B

In questo caso il problema sembra essere
impossibile
|
Caso C

In questo caso il problema si può risolvere
partendo da qualunque punto
|
Domande
E' vero che il caso B è impossibile?
Come si può dimostrarlo?
Cosa c'é di sostanzialmente diverso fra i tre casi?
Come si possono distinguere i problemi possibili da
quelli impossibili?
Esiste una strategia che aiuti a risolvere i problemi
di questo tipo?
Una piccola sfida
Altri esercizi
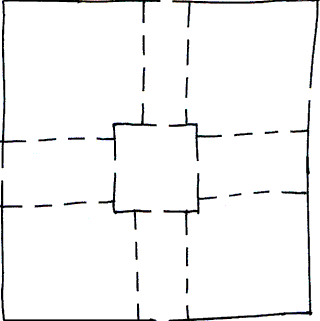
Esercizio 1
Grazie a Giovanni R., classe 1°B
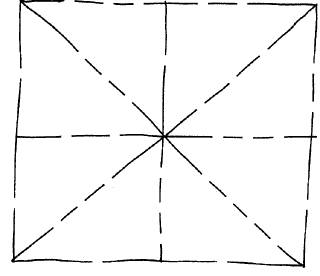
Esercizio 2
Grazie a Israel T., classe 1B
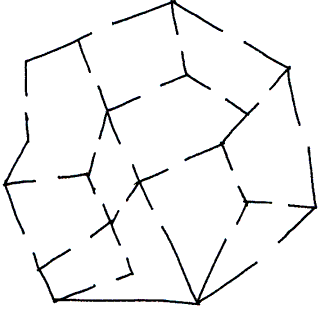
Esercizio 3
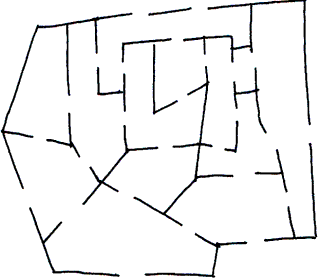
Esercizio 4
Data creazione: gennaio 2006
Ultimo aggiornamento: aprile 2006
Risposte & riflessioni
Il problema delle cinque camere (A)
Questa è una possibile soluzione del primo problema. La soluzione non può
essere rappresentata da una linea chiusa.
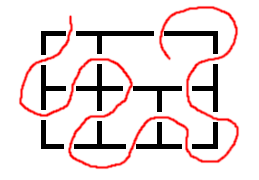
Il problema delle cinque camere (B)
Il secondo problema è un classico "problema impossibile". Non si può
risolvere sul piano. Naturalmente, tanto per cambiare, si può risolvere su un
toro! Ma il "buco della ciambella" deve essere in un punto ben preciso!
Il problema delle sei camere (C)
Il problema si può risolvere partendo da qualunque punto. Infatti la
soluzione può essere rappresentata da una linea chiusa.

Domande
Come si può dimostrare che il caso B è impossibile?
...?
Esiste un metodo semplice e veloce per distinguere i
problemi risolvibili da quelli impossibili?
Certamente! Ecco come procedere.
1) Prima di tutto notate che, se ci sono porte che si aprono
verso l'esterno, allora dovete considerare una camera in più. La
parte di piano esterna all'appartamento deve essere considerata come una
camera. Nel nostro caso avete quindi 6 camere.

Questo problema è impossibile perché ci sono
quattro camere con un numero dispari di porte
2) Scrivete all'interno di ogni camera il numero delle porte
che accedono ad essa.
3) E ora, finalmente, la regola:
a) se tutti i numeri che avete scritto sono pari, potete risolvere il
problema partendo da una camera qualsiasi;
b) se compaiono esattamente 2 numeri dispari, potete risolvere il problema
partendo da una delle due camere con un numero dispari di porte e terminando
nell'altra;
se compaiono più di 2 numeri dispari, il problema è impossibile.
Come si può dimostrare questa regola?
...?
Una piccola sfida
Credo che purtroppo sia impossibile disegnare un appartamento in cui una
sola camera abbia un numero dispari di porte e tutte le altre ne abbiano un
numero pari. Tuttavia i miei alunni (della scuola secondaria di 1° grado),
nei loro tentativi, sono arrivati a risultati interessanti, come il seguente
(grazie Walter P. (3° media)!).

Il problema è che passando attraverso la porta A non si
cambia camera ma si rimane all'interno della stessa camera.
Questo esempio ci aiuta a definire meglio il problema:
ogni porta deve mettere in comunicazione due camere diverse.
Grazie a Giordano B. (1° media) che mi ha inviato il
seguente bellissimo disegno.
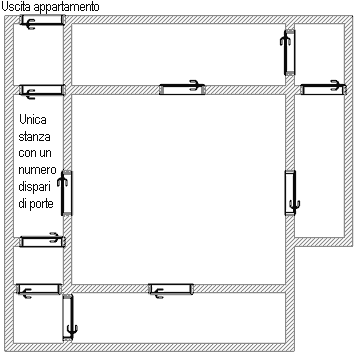
Effettivamente sembra esserci una una unica camera con un numero dispari
di porte (3).
Ma c'é anche una porta di uscita dall'appartamento.
In questo caso, anche la parte di piano ESTERNA all'appartamento deve essere
considerata come una camera. Ma QUESTA camera ha una porta, che è un numero
dispari.
In conclusione l'appartamento ha 2 camere con un numero dispari di porte.
Perciò il problema rimane ancora irrisolto.
Altri esercizi
Esercizio 1
E' risolvibile
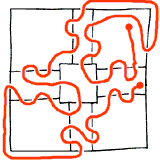
Esercizio 2
E' risolvibile
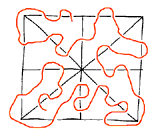
Esercizio 3
Non è risolvibile
Esercizio 4
E' risolvibile
Sito Web realizzato da Gianfranco Bo

















