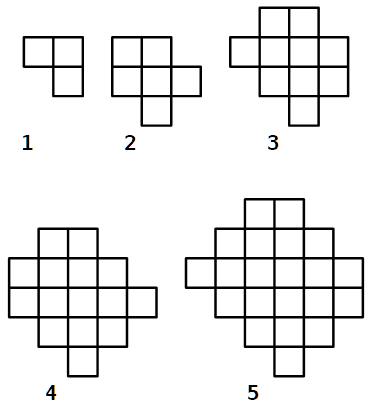
[BASE Cinque - Appunti di Matematica ricreativa]

Le reti dei bambini Kuba

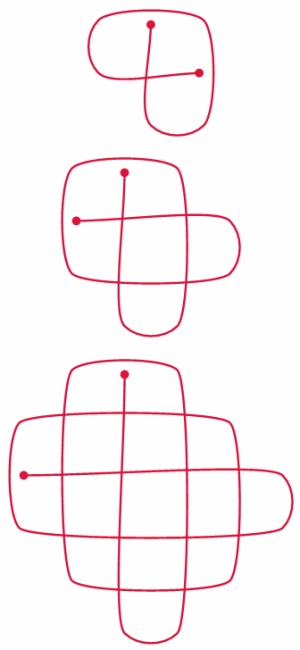
Ecco una sequenza di figure sempre più grandi.

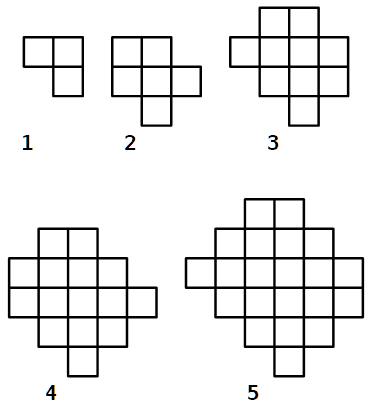
Provate a disegnare ciascuna figura seguendo queste regole:

1. non dovete mai staccare la penna dal foglio;
2. non dovete passare su un segmento più di una volta;
3. potete passare sugli incroci delle linee;
4. segnate il punto di partenza e quello d'arrivo.

Esplorazioni:

a) Quali sono i punti di partenza buoni? Quali i punti di arrivo?

b) C'è una regola per trovarli subito senza fare tentativi?

c) Continuate la sequenza disegnando figure più grandi.

d) Trovate un metodo facile da ricordare per tracciare velocemente queste figure, in modo da meravigliare chi vi sta osservando.

---

I bambini del popolo Kuba (Congo) sono abilissimi a tracciare questi disegni sulla sabbia usando un dito invece della penna.

---

Note.

Questa attività è proposta da Claudia Zaslavsky nel suo libro Multicultural Mathematics. Interdisciplinary Cooperative-Learning Activities, 1987,1993, pag. 115.

Claudia Zaslavsky racconta un aneddoto sull'antropologo culturale Emil Torday che visse alcuni anni tra i Kuba, in Congo, all'inizio del XX secolo.

Un giorno Torday vide alcuni bambini che facevano dei disegni nella sabbia.
Lo invitarono a copiare quei disegni senza mai alzare il dito dalla sabbia né passare su un segmento più di una volta.
Egli scrisse in un suo libro che erano "esercizi impossibili". 

Per altri esempi e per un approfondimento sui cammini euleriani nei grafi potete vedere: Senza staccare la penna dal foglio.

Risposte & riflessioni

a) Le figure si possono tracciare solo partendo da uno dei due punti segnati con un bollino e arrivando all'altro punto.

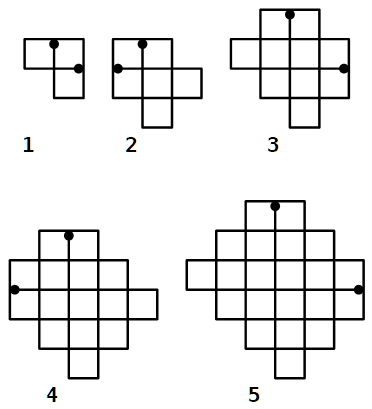
b) Possiamo interpretare questi disegni come grafi che hanno esattamente due nodi dispari, che sono quelli evidenziati.

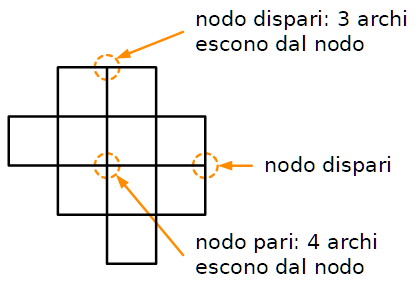
I grafi di questo tipo si possono percorrere con un unico tratto partendo da un nodo dispari e arrivando all'altro.

Un percorso che passa per tutti gli archi di un grafo una e una volta sola si chiama cammino euleriano.

d) Le seguenti figure indicano meglio il percorso della penna.
Ogni disegno si può tracciare velocemente se lo immaginiamo come una specie di spirale che si intreccia.

A seconda del punto di partenza, la "spirale" va tracciata in senso orario oppure anti-orario.

---

Pace e bene a tutti.

GfBo

Data creazione: maggio 2021

Ultimo aggiornamento: luglio 2021

html5

Sito Web realizzato da Gianfranco Bo