[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Giochi con l'anello di Moebius

C.M.Escher, Striscia di Moebius II, xilografia, 1963

1. Costruire un anello di Moebius
Ecco come potete costruire un anello di Moebius:
1) ritagliate una striscia di carta di circa 3x30 cm.
2) tenendola per le estremità datele una torsione di 180°
3) piegatela in modo da formare un anello, unite le estremità e incollatele.

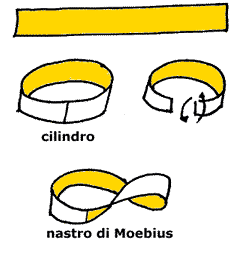
2. Stirare un anello di Moebius

3. Disegnare una linea lungo il cilindro
L'anello di Moebius è una superficie che ha una sola faccia. Per capire questa sua singolare proprietà si può metterlo a confronto con una superficie cilindrica. La superficie cilindrica ha due facce: quella esterna e quella interna. Se tracciate una linea continua lungo tutta la faccia interna di un cilindro, vi ritroverete al punto di partenza dopo aver descritto una linea chiusa che giace interamente sulla faccia interna del cilindro.

4. Disegnare una linea lungo l'anello di Moebius
Se invece tracciate una linea continua lungo tutto l'anello di Moebius, anche in questo caso tornerete al punto di partenza, ma se aprite l'anello vedrete con grande sorpresa che la penna ha percorso interamente entrambe le facce della striscia di carta. La conclusione matematica è che l'anello di Moebius non ha due facce, bensì una sola!

5. Tagliare a "metà" l'anello di Moebius
Se ritagliate un anello di Moebius lungo la linea mediana come illustrato nella fig.4, che cosa ottenete? Due anelli di Moebius? O forse due cilindri?

6. Anelli incrociati
Utilizzando due strisce di carta, preparate un modello come illustrato nella figura qui sotto e ritagliatelo lungo le linee tratteggiate. Che cosa ottenete?

7. Anelli incrociati 2
Utilizzando due strisce di carta, preparate un modello come illustrato nella figura qui sotto e ritagliatelo lungo le linee tratteggiate. Che cosa ottenete?

8. Costruire un doppio anello di Moebius
Provate a costruire un doppio anello di Moebius con due strisce di carta uguali sovrapposte. Date loro una torsione di 180° e incollate le estremità come illustrato nella figura qui sotto. Che cosa avete ottenuto? Due anelli di Moebius uno dentro l'altro? Per scoprirlo provate a separarli.

9. Colorare le mappe sull'anello di Moebius
Nel 1840 August Moebius pose il seguente problema sotto forma di favola:

"C'era una volta un re che aveva cinque figli. Egli stabilì che alla sua morte il regno fosse suddiviso tra i figli in cinque regioni in modo che ciascuna regione confinasse con le altre quattro. E' possibile esaudire la sua richiesta?"

Questa è la storia originale di Moebius.
Ma il re visse ancora a lungo ed ebbe un altro figlio. E' possibile dividere il regno in 6 regioni in modo che ciascuna di esse abbia almeno una linea di confine con ciascuna delle altre 5?

10. L'anello di Moebius e il logo del riciclaggio
Certamente tutti conoscete il simbolo del riciclaggio dei rifiuti. Tuttavia ad un'attenta osservazione si scopre che ne esistono versioni molto differenti dal punto di vista topologico. Potete vedere due esempi nelle figure qui sotto. Quale delle due rappresenta un anello di Moebius?

Nota storica: L'anello di Moebius è chiamato così in onore dell'astronomo tedesco August Ferdinand Moebius che per primo ne studiò le proprietà nel 1858.

Risposte & riflessioni

1. Costruire un anello di Moebius

2. Stirare un anello di Moebius

3. Disegnare una linea lungo il cilindro

4. Disegnare una linea lungo l'anello di Moebius

5. Tagliare a "metà" l'anello di Moebius

6. Anelli incrociati 1

7. Anelli incrociati 2

8. Costruire un doppio anello di Moebius

9. Colorare le mappe sull'anello di Moebius

10. L'anello di Moebius e il logo del riciclaggio

Sito Web realizzato da Gianfranco Bo