Un nodo magico

Il problema "Come appendere un quadro in modo stupido" posto da Francesco Veneziano al Forum mi ha fatto venire in mente questo gioco di prestigio di cui avevo letto tanti anni fa su un libro di Martin Gardner. Credo che fosse uno dei suoi volumi intitolati "Enigmi e giochi matematici".

Se volete provarlo, seguite le immagini e le istruzioni.
Per una buona riuscita è meglio essere in due e si può utilizzare una matita al posto dell'asta di legno.
Uno tiene la matita e la striscia di carta e l'altro manovra lo spago.

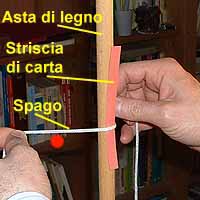1. Appoggiate una striscia di carta ad un'asta di legno e iniziate ad avvolgere lo spago. Il bollino rosso indica sempre lo stesso tratto dello spago. Nota bene: il tratto indicato dal bollino deve sempre essere avvolto SOPRA = PIU' IN ALTO (oppure SOTTO) dell'altro tratto di spago. Cioè deve rimanere sempre dalla stessa parte.	2. Fate con lo spago un giro completo attorno all'asta.
3. Proseguite fino a fare con lo spago due giri completi attorno all'asta.	4. Ripiegate, con l'aiuto di un amico, la striscia di carta sopra lo spago avvolto. Avvolgete lo spago alla striscia invertendo il senso della rotazione.
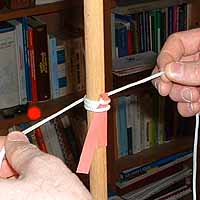5. Date ancora un giro di spago attorno all'asta. Ricordate che il tratto segnato dal bollino deve rimanere sempre al di sopra (più in alto) rispetto all'altro tratto di spago.	6. Impugnate saldamente lo spago ai due capi e tendetelo energicamente, con un forte strattone. La striscia di carta sarà strappata in due parti e cadrà a terra e lo spago non sarà più avvolto all'asta!

Abbiamo un quadro, due chiodi piantati in un muro e un filo sufficientemente lungo legato ai due angoli superiori del quadro.
Nella nostra perversione vogliamo appendere il quadro in modo che staccando dal muro uno qualunque dei due chiodi, il quadro cada.

La soluzione è "onesta" e non prevede che gli estremi del filo vengano staccati dagli angoli del quadro, né che i chiodi vengano estratti dal muro e ripiantati, né che il quadro venga appoggiato sui chiodi, che potrebbero anche essere disposti verticalmente.
Il filo è da considerarsi perfettamente liscio e privo di attrito, quindi eventuali nodi sono liberi di scorrere.

Il problema può essere generalizzato a n chiodi.

Risposte & riflessioni

Riporto la soluzione di Pasquale.
Caso semplificato di due chiodi orizzontali:

Appoggio il filo sui due chiodi.
Prendo il capo verticale discendente dal primo chiodo e, passando da sotto al primo chiodo, l'appoggio sul secondo chiodo
Prendo l'altro capo verticale discendente dal secondo chiodo ed opero simmetricamente come prima.
Con ognuna delle due operazioni libero un chiodo dalla regione chiusa filo-quadro, assimilabile topologicamente ad un cerchio: all'apparenza non sembra, ma togliendo un chiodo appare chiaro.

Con questi disegni mi sembra di interpretare la soluzione di Pasquale.
Nel caso A libero il chiodo 2. Se tolgo il chiodo 1 il quadro precipita.
Nel caso B libero il chiodo 1. Se tolgo il chiodo 2 il quadro precipita.
Nel caso C libero entrambi i chiodi. Se tolgo un chiodo qualsiasi il quadro precipita.