[BASE Cinque - Appunti di Matematica ricreativa]
Il pretzel o brezel è un tipo di pane formato da un cordoncino di pasta intrecciato come si vede nella figura qui sotto.
E' anche il nome della forma geometrica n.1, formata da due anelli incatenati collegati fra loro con un cilindro.
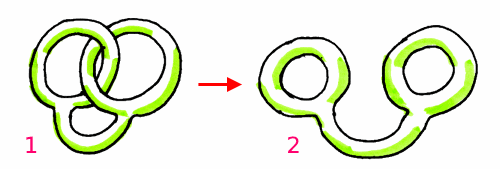
Le due forme sono topologicamente equivalenti, ma come si fa a trasformare la forma 1 nella forma 2 con una deformazione continua, senza tagliare un anello?
Prima di procedere, è meglio studiare il seguente articolo di Gino Fano per farsi un'idea di equivalenza topologica e di trasformazione continua.
Gino Fano. L'analysis situs I. Scientia, Vol. 36 (1924), p. 217–230 (PDF)
Intuitivamente, una trasformazione continua si realizza facendo deformazioni arbitrarie, purché fatte senza strappi o lacerazioni, né saldature nella superficie della forma.
Consideriamo solo la superficie delle forme, non il loro interno. Possiamo imaginarle come dei palloncini gonfiati, la cui superficie sia illimitatamente elastica.
Se due forme si possono trasformare l'una nell'altra con deformazioni continue, allora sono topologicamente equivalenti.
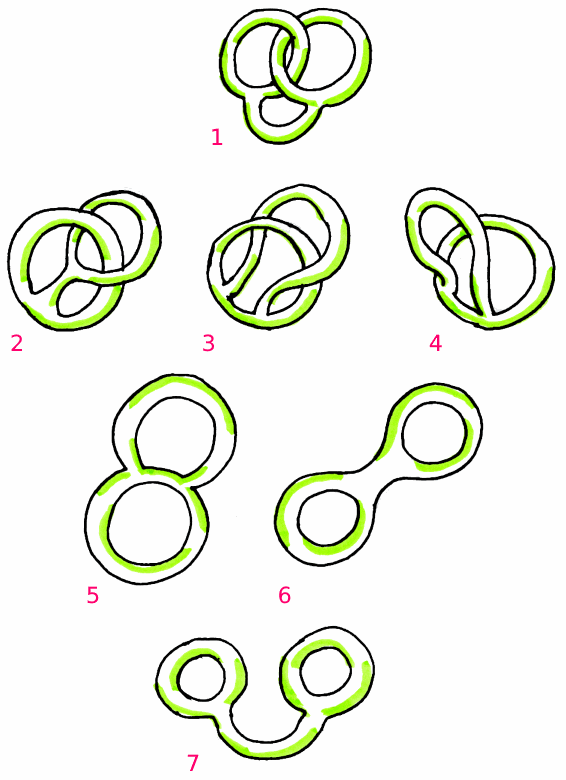
Per esempio, le seguenti forme 1, 2, 3 sono topologicamente equivalenti.
Da notare che il passaggio da 2 a 3 NON comporta lacerazioni della superficie.

Ecco una serie di figure topologicamente equivalenti al pretzel.
Provate a costruire mentalmente tutte le trasformazione dall'una all'altra.
In particolare, la n. 6 è un bi-toro (toro doppio) e la n. 8 è una sfera con 2 manici.
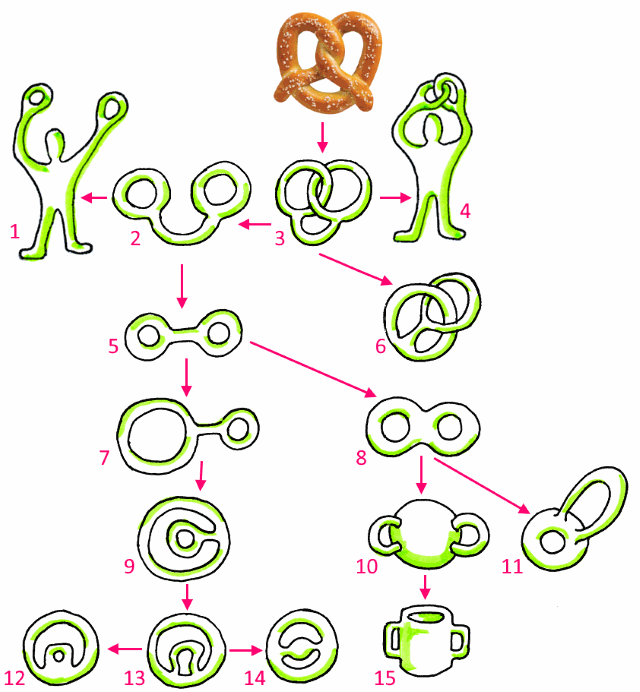
Ecco una possibile soluzione.
Ed ecco un'altra soluzione, scherzosa ma esatta.
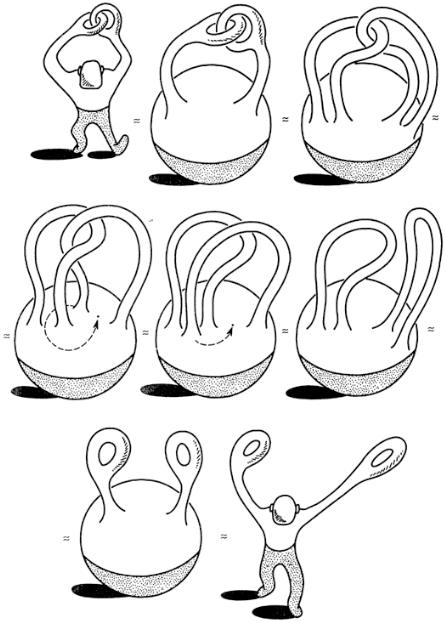
Credit: http://dfgm.math.msu.su/topics/topic07.php
Un'altra simile.
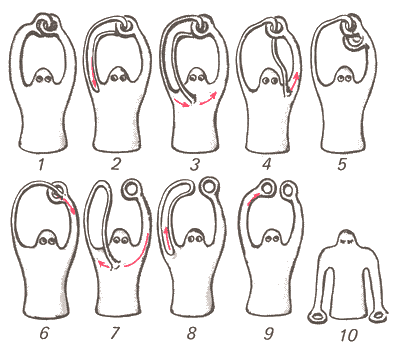
Credit: https://kvantik12.livejournal.com/6239.html
Ancora una, molto semplice da intuire.
Si legge in senso anti orario (mentre quello orario rappresenta la trasformazione inversa)
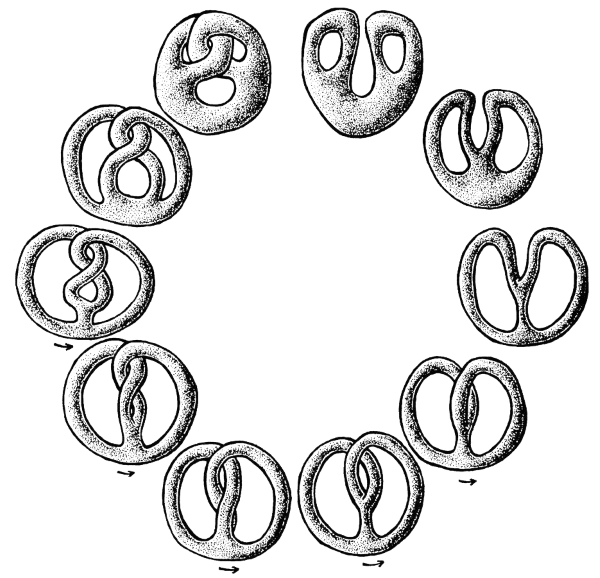
Credit: https://spring-of-mathematics.tumblr.com/
...
Pace e bene a tutti!
Gianfranco Bo
Data creazione: giugno 2019
Ultimo aggiornamento: giugno 2019
xhtml 1.1
Sito Web realizzato da Gianfranco Bo