[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Il teorema dei 4 colori
...ed oltre
| Ricordate quelle vecchie e
decoratissime carte geografiche dell'Italia, in cui
le varie regioni erano rappresentate con colori diversi?
Ne ho una davanti agli occhi. Il Lazio e la Puglia, che
non confinano fra di loro, sono gialle. L'Umbria e
il Molise sono verdi. La Toscana, che confina sia con l'Umbria
che con il Lazio, non deve essere né gialla né verde:
è colorata di rosa. Le Marche, che confinano con l'Umbria,
il Lazio e la Toscana, non devono essere né rosa né
verdi né gialle ed infatti sono colorate di marroncino. |

|
| Dal punto di vista
matematico la situazione può essere rappresentata con il
disegno qui sotto. La regola fondamentale per colorare le
mappe è che due regioni (o aree) confinanti non devono
essere colorate dello stesso colore. Due regioni che si
toccano solo per un punto non sono considerate confinanti. Quanti
colori servono, come minimo, per colorare una mappa
qualsiasi?
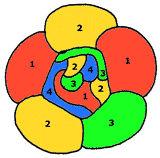
Il teorema dei 3 colori
Esistono mappe che richiedono più
di 3 colori.
Osservate il disegno: sareste capaci di colorarlo con
soli 3 colori?
Non è possibile perché ciascuna delle 4 regioni confina
con le altre tre.
|

|
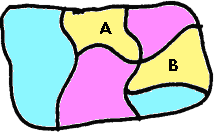
Questa mappa è colorata correttamente perché le
regioni A e B hanno in comune un solo punto.
|
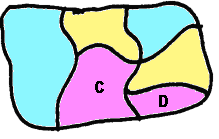
In questa mappa c'è un errore di colorazione
perché le regioni C e D confinano lungo una linea e
quindi devono essere di colori diversi.
|
Ed ora qualche esercizio. Colorate le cinque mappe con il
numero di colori indicato.
Prima di procedere alla colorazione conviene segnare le
regioni con numeri. In questo modo è più facile correggere
gli eventuali errori.
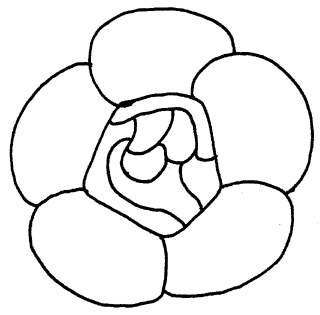
Con 2 colori

Questa mappa, anche se sembra complicata, è colorabile
con soli 2 colori
Sapete trovare un criterio generale per costruire mappe a due
colori?
Con 3 colori

Con 4 colori


Risposte & riflessioni

Il teorema dei 2 colori
Se una mappa è delimitata soltanto da linee che si
incrociano e nessuna linea si interrompe quando interseca un'altra
linea, allora due colori sono sufficienti per colorarla.
Con 3 colori

Con 4 colori
Il teorema dei 4 colori
Quattro colori sono sufficienti per colorare qualsiasi mappa
piana.
Come abbiamo visto, esistono
mappe colorabili con 2 o 3 colori soltanto. Ma non esiste
nessuna mappa piana che necessiti di più di quattro colori
diversi.
Il problema dei quattro colori
nacque nel 1852 quando Francis Guthrie, basandosi sull'esperienza
dei cartografi, formulò la congettura che 4 colori fossero
sufficienti per colorare qualsiasi mappa piana.
Il problema, a prima vista così
semplice, si rivelò invece molto difficile e solo nel 1976
Kenneth Appel and Wolfgang Haken dell'Università dell'Illinois
riuscirono a dimostrarlo con l'aiuto del computer.
Il teorema vale per le mappe disegnate sul
piano, ma che dire delle mappe disegnate su un anello di
Moebius o su un toro?
Sito Web realizzato da Gianfranco Bo