[BASE Cinque - Appunti di Matematica ricreativa]
Dove finisce il gioco e dove comincia la matematica "seria"?
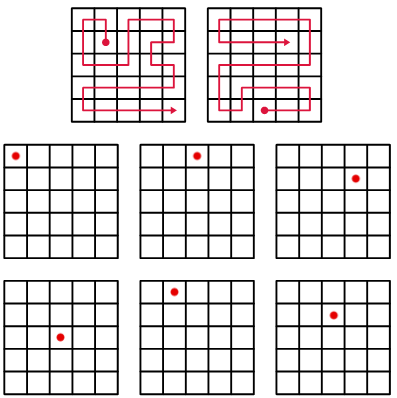
Ecco il problema, posto solo con un disegno, senza parole.

Questo tipo problema appartiene alla matematica ricreativa da almeno 100 anni ma la fonte principale che mi ha spinto a riprenderlo è l'articolo di James Tanton, Personal stories of discovering mathematics, su Medium, 2018.
...
Un po' di righe vuote.
...
La soluzione è più avanti.
...
La soluzione è solo una traccia di un possibile percorso.
...
...
...
I disegni sembrano un invito a tracciare un percorso continuo che attraversi tutti i quadratini della griglia (celle) una sola volta.
Il punto di partenza è irresistibilmente segnato con un bollino rosso.
Facciamo delle prove.
In quattro casi, troviamo una o più soluzioni.
In due casi, anche dopo molti tentativi, non riusciamo a trovare alcuna soluzione.
Almeno una cella rimane fuori dal percorso.
Con un po' di pazienza e usando le simmetrie scopriamo che ci sono 13 celle nella griglia dalle quali è possibile tracciare un percorso come quello richiesto.
Osserviamo che bastano solo i quattro esempi dati per trovare tutte le celle di partenza "buone".
Usando le simmetrie e le rotazioni, scopriamo che ci sono 12 celle per le quali NON riusciamo tracciare il percorso richiesto.
Anche in questo caso, i due esempi dati bastano per trovare tutte le celle di partenza "NON-buone".
A questo punto, definiamo meglio il problema.
Problema.
E' data una griglia quadrata di 5x5 celle.
Fra le 25 celle della griglia se ne sceglie una.
Si chiede di:
Il matematico la pensa così:
Nel nostro caso, sospettiamo che, partendo da alcune celle, non sia possibile trovare un cammino continuo che attraversi tutte le celle della grigila una sola volta.
Non è facile dimostrarlo per la griglia 5x5.
Allora facciamo come i matematici: partiamo da una situazione più semplice.
Esaminiamo per esempio le griglie di 2x2, 3x3, 4x4 celle e vediamo cosa succede.
Griglia 2x2
Osserviamo che si può tracciare un percorso chiuso (ad anello) che passa una sola volta per tutte le celle.
Quindi ogni cella può essere l'origine del cammino e la cosa funziona sempre.
Griglia 3x3
Come nel caso 5x5 ci sono punti di partenza buoni e punti non buoni.
Griglia 4x4
Osserviamo che, come nella griglia 2x2, si può tracciare un cammino chiuso perciò, anche qui tutte le celle sono "buone" come punti di partenza.
Ci viene il sospetto che per n pari il problema è sempre risolvibile.
Decidiamo di studiare il caso 3x3, più semplice del 5x5.
Sia qui, sia nel caso del 5x5 salta agli occhi che le celle "buone" e quelle "non buone" formano una scacchiera.
Prendiamo lo spunto e coloriamo le celle di bianco e grigio, come una scacchiera.
Sappiamo per esperienza che, nella colorazione qui sotto, le celle grigie sono "non buone". Teniamolo presente.
Osserviamo che:
Immaginiamo di "distendere" un percorso mettendo in riga le celle via via attraversate.
Se si parte da una cella bianca, la cosa funziona perché si inizia dal bianco e si termina sul bianco.
Se invece si inizia da una cella grigia, la cosa NON può funzionare.
Infatti, l'ottava (9-1) cella del cammino è necessariamente bianca e quindi l'ultima dovrebbe essere grigia, ma sulla griglia è rimasta solo una cella bianca. Quelle grigie le abbiamo già percorse tutte.
Quindi il cammino non si può completare secondo le regole date.
Lo stesso ragionamento si estende facilmente e tutte le griglie n x n, con n dispari.
Ecco un problema posto da Henry Ernest Dudeney.
La figura è una mappa geografica. I quadrati rappresentano 64 città e i segmenti rappresentano le strade che collegano le città.
Il quadrato nero è la città di partenza.
Il compito è quello di tracciare il percorso di un pellegrinaggio che parta dalla città di partenza e passi attraverso tutte le altre città, ciascuna una sola volta.
La linea che descrive il cammino deve essere formata da 15 segmenti.
In fondo manca un segmento. L'omissione è intenzionale, non è un errore.
Ecco il testo originale.
The gentle Pardoner, "that straight was come from the court of Rome," begged to be excused; but the company would not spare him. "Friends and fellow-pilgrims," said he, "of a truth the riddle that I have made is but a poor thing, but it is the best that I have been able to devise. Blame my lack of knowledge of such matters if it be not to your liking." But his invention was very well received. He produced the accompanying plan, and said that it represented sixty-four towns through which he had to pass during some of his pilgrimages, and the lines connecting them were roads. He explained that the puzzle was to start from the large black town and visit all the other towns once, and once only, in fifteen straight pilgrimages. Try to trace the route in fifteen straight lines with your pencil. You may end where you like, but note that the omission of a little road at the bottom is intentional, as it seems that it was impossible to go that way.
Tratto da: The Project Gutenberg eBook of The Canterbury Puzzles, by Henry Ernest Dudeney
Ed ecco la soluzione.
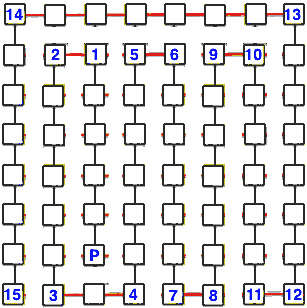
Grazie a Giobimbo per la soluzione dal Forum.
Dipende.
Lascio la risposta a ciascuno di voi.
La mia risposta è: il gioco non finisce mai e la matematica seria comincia subito.
Purtroppo ci sono situazioni in cui si usa la matematica per scopi malvagi: in tal caso il gioco non comincia mai e la matematica seria finisce subito.
---
Pace e bene a tutti!
Gianfranco Bo
Data creazione: gennaio 2019
Ultimo aggiornamento: gennaio 2019
xhtml 1.1
Sito Web realizzato da Gianfranco Bo