[BASE Cinque - Appunti di Matematica ricreativa]
1 GENNAIO 2019
Cari amici, ho consultato l'OEIS a proposito del 2019 e vi comunico con piacere che:
perciò possiamo stare tranquilli: il 2019 sarà un anno felice e forunato per tutti!
Ecco altre due curiosità.
E' un numero semprimo cioè è il prodotto di due soli numeri primi (https://oeis.org/A001358):
2019 = 3 × 673
E' un numero composto tale che ogni concatenazione dei suoi fattori primi è un numero primo (https://oeis.org/A217263)
3673 è primo, 6733 è primo.
BASE Cinque augura un prospero 2019 all'OEIS, inesauribile miniera di preziose informazioni per i matematici di tutto il mondo.
The On-Line Encyclopedia of Integer Sequences® (OEIS®)
12 DICEMBRE 2018
Si possono proporre esercizi di matematica ricreativa su Twitter, usando non più di 280 caratteri + una figura?
Catriona Shearer ci riesce benissimo con i suoi deliziosi puzzles di geometria. (twitter.com/Cshearer41)
Ne ho scelto tre che si possono fare a mente. Ho anche confrontato il numero di caratteri in inglese e italiano. Se qualcuno sa essere più breve, è il benvenuto.
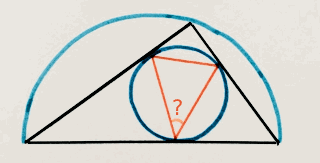
Puzzle 1.
Un triangolo in un cerchio in un triangolo in un semicerchio... quanto è ampio l'angolo?
(88 caratteri)

A triangle in a circle in a triangle in a semicircle... what’s the angle? (73 caratteri)
Puzzle 2.
Quale frazione dell'esagono è colorata? L'esagono è regolare, i punti sono disposti a intervalli regolari sul suo perimetro.
(124 caratteri)
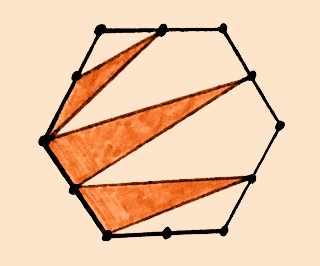
What fraction is shaded? The hexagon is regular, with equally spaced dots around its perimeter. (95 caratteri)
Puzzle 3.
Tre rettangoli congruenti di area 4 sono sovrapposti come vedi nella figura. I punti neri indicano i punti medi dei lati corti.
Quale area totale è coperta dai tre rettangoli? (175 caratteri)
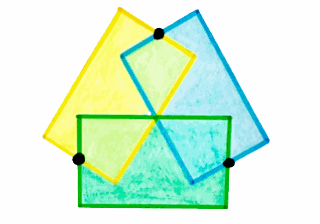
These three overlapping rectangles are congruent, each wth area 4. The black dots mark the midpoints of the short sides. What total area is covered by this design? (163 caratteri).
11 NOVEMBRE 2018
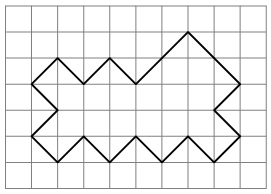
Questo problema è tratto dal Monday Puzzle di Alex Bellos su "The Guardian" del 22 ottobre 2018. (www.theguardian.com/science/series/alex-bellos-monday-puzzle)
Siete capaci di tagliare la forma in due parti congruenti fra loro e simili alla figura di partenza?
Potete usare solo una linea, non necessariamente retta.
10 OTTOBRE 2018
Ci sono molti esercizi sul teorema di Pitagora NEL cubo.
Questo è un esercizio sul teorema di Pitagora FUORI DAL cubo.
La figura rappresenta una struttura di 8 cubi uguali, di lato 10 cm.
Una mosca ideale fa un volo perfettamente rettilineo dal vertice A al vertice B.
Quanto è lungo il volo della mosca?
24 SETTEMBRE 2018
Segnalo un'iniziativa molto promettente per migliorare l'insegnamento e l'apprendimento delle materie scientifiche.

http://www.dowellscience.eu/project/
Il progetto europeo DoWellScience è finanziato dal programma Erasmus+, KA2 – Parternariati Strategici nell’ambito della Formazione Scolastica.
Ha l'obiettivo di migliorare i risultati e le performance degli studenti di scuola superiore nelle discipline STEM (scienza, tecnologia, ingegneria e matematica).
E' coordinato scientificamente dal Liceo Statale Niccolò Machiavelli di Firenze, in partnership con il Dipartimento di Matematica dell'Università di Genova, il Technological Educational Institute (TEI) di Messolongi (Grecia), la Södertörn University (Svezia), la John Atanasoff Vocational High School of Electronics (Bulgaria), la Zinev Art Technologies Ltd. (Bulgaria), l'Arsakeio Lyceum of Patra (Grecia),
8 AGOSTO 2018
Ho già parlato di speranza matematica nella Mini-teoria della probabilità.
Qui vi propongo alcuni problemi nuovi.
---
PROBLEMA 1 (UNA VINCITA POSSIBLE)
Consideriamo il gioco seguente.
Regole:
Quanto puoi sperare di vincere a questo gioco?
ATTENZIONE: la domanada NON è quanto puoiì sperare di vincere se giochi una volta. In questo caso c'è poco da sperare: o vinci 5 € o perdi. La probabilità è 50%-50%.
Il senso della speranza matematica invece è: se giochi moltissime partite, quanto puoi sperare di vincere in media in ogni partita?
Precisiamo meglio la domanda: quale vincita media ti aspetti per ogni partita giocata?
Per rispondere, usiamo questa definizione:
| Speranza matematica (1).
La speranza matematica E di una vincita X è il prodotto del valore x della vincita per la probabilità di vincerla p(x). E(X) = x·p(x) |
La speranza matematica si chiama anche media o valore atteso di una variabile casuale.
Nel nostro caso, in una partita possiamo vincere 5 € con probabilità 1/2,
perciò la speranza matematica è:
E(X) = 5 · 1/2 = 2,50 €
---
PROBLEMA 2 (DUE VINCITE E UNA PERDITA POSSIBILI).
Consideriamo il gioco seguente.
Regole:
Qual è la speranza matematica di vincita?
Estendiamo la precedente definizione.
Speranza matematica (2). La speranza matematica E di una vincita X è la somma dei prodotti del valore xi di ogni possibile vincita per la rispettiva probabilità di vincerla pi. E(X) = x1·p1 + x2·p2 + x3·p3 + ... |
Nel nostro caso, in una partita possiamo vincere 5 € con
probabilità 1/4 oppure vincere 2 € con probabilità 1/2
oppure perdere 7 € con probabilità 1/4, perciò la speranza
matematica è:
E(X) = 5 · 1/4 + 2 · 1/2 + (-7) · 1/4 = 0,50 €
Come si vede, anche se rischiamo di perdere ogni tanto 7 €, la speranza matematica di vincere a questo gioco è positiva.
Facendo molte partite, vinceremo in media 0,50 € a partita.
---
PROBLEMA 3 (CONTINUA FIN QUANDO PERDI).
Consideriamo il gioco seguente.
Regole:
In altre parole il gioco va avanti e continui a vincere fino a quando esce "GAME OVER"
Qual è la speranza matematica di vincita a questo gioco?
In questo caso, la risposta è più difficile perché in una partita può
capitare di far girare la ruota una o più volte, illimitatamente.
Allora, come si fa?
In attesa della continuazione, potete dare un'occhiata al Forum, qui: Vincita attesa.
7 LUGLIO 2018
Questo teorema è una piccola sorpresa che, a prima vista, sembra difficile da dimostrare. In realtà, se ci giocate un po', una dimostrazione arriva facilmente.
---
Teorema: La somma dei quadrati di due numeri di Fibonacci consecutivi è un numero di Fibonacci.
(Fn)2 + (Fn+1)2 = F2n+1
Questa proprietà si può rappresentare con un triangolo rettangolo, così.
Cissà se ci sono collegamenti più profondi...
---
Memo. Ricordo la sequenza di Fibonacci:
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Ogni numero (dal 3° in avanti) è la somma dei due numeri che lo precedono:
Fn = Fn-1 + Fn-2
Attenzione a non fraintendere: i tre numeri di Fibonacci assomigliano a una terna pitagorica ma non lo sono!
Anzi, non esistono tre numeri di Fibonacci che formano una terna pitagorica (a parte un caso particolare).
Tratto dal blog di John D. Cook, https://www.johndcook.com/blog/2018/07/13/fibonacci-meets-pythagoras/
6 GIUGNO 2018
Una capra è legata a un angolo esterno di un fienile quadrato di lato 10 m.
Tutto intorno c'è un immenso pascolo pianeggiante.
Qual è l'area massima che la capra può pascolare (esternamente al fienile) se la corda è lunga x?
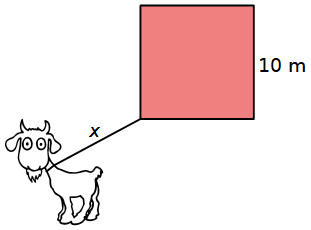
Chiave di ricerca per questa classe di problemi: "grazing area math problem".
La versione più vecchia che ho trovato in Internet è del 1995 e si trova sul Math Forum:
http://mathforum.org/dr.math/faq/faq.grazing.html
Se la lunghezza x della corda va da 0 a 10 m, la superficie massima che la capra può pascolare è pari a 3/4 di un cerchio di raggio x.
Se la lunghezza x della corda va da 10 a 20 m, la superficie massima di pascolo è pari a 3/4 di un cerchio di raggio x più mezzo cerchio di raggio (x-10).
Se la lunghezza x della corda supera il doppio del lato, per esempio è 30 m, il problema si complica perché ci sono superfici che si sovrappongono.
In questo caso la superficie massima di pascolo è formata da 3/4 di un cerchio di raggio x più due settori uguali di raggio (x-a) più un quadrilatero deltoide concavo.
Bisogna concentrarsi sull'area del quadrilatero, il resto è semplice.
5 MAGGIO 2018
Le seguenti forme sono costruite usando soltanto dei rettangoli.
La sfida è trovare il valore mancante segnato con un punto interrogativo.
Ecco un esempio con una strategia risolutiva.
Esistono altre strategie, create la vostra.
Ecco altri quattro esercizi.
1. Il capostipite
2. Con due rettangoli
3. Scaletta
4. Un po' più difficile
E' interessante risolvere questi esercizi mentalmente, senza carta né matita né calcolatrice.
4 APRILE 2018
Quanto fa la somma S di questa serie formata da una sequenza illimitata di +1 e -1?
Allora, se uso la proprietà associativa (illimitatamente) così:
S = (1 - 1) + (1 - 1) + (1 - 1) + ... = 0 + 0 + 0 + ... = 0
Se invece la uso così:
S = 1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + ... 1 + 0 + 0 + 0 + ... = 1
Se uso la proprietà commutativa (illimitatamente) e quella associativa così:
1 + 1 - 1 + 1 - 1 + 1 - 1 + ... =
S = (1 + 1) + (-1 + 1) + (-1 + 1) + ... = 1 + 1 + 0 + 0 + 0 + ... = 2
OK, posso ottenere qualunque numero naturale come risultato della somma.
Ma posso ottenere anche 0,5 con i più svariati ragionamenti.
Per esempio, se applico (illimitatamente) la proprietà distributiva della moltiplicazione rispetto all'addizione ottengo:
S = 1 - 1 + 1 - 1 + 1 - 1 + 1 - ... ma anche...
S = 1 - (1 - 1 + 1 - 1 + 1 - 1 + ... ) = 1 - S
Da cui:
S = 1 - S
2S = 1
S = 1/2 = 0,5
Qual è la morale di tutto ciò?
La morale è che non si possono applicare impunemente le proprietà delle operazioni in modo illimitato per calcolare la somma di una serie infinita. Tali proprietà valgono soltanto per un numero limitato di termini.
Ma se voglio sapere qual è la somma della serie?
Si deve estendere la definizione di somma in modo che dia un risultato anche in questi casi strani. Però tale nuova definizione deve essere compatibile con la vecchia definizione.
Per chi vuole approfondire:
a) la serie 1 - 1 + 1 - 1 +... si chiama serie di Grandi.
b) il metodo più semplice e corretto di calcolare la somma della serie di Grandi è la somma di Cesàro.
c) e finalmente, il valore corretto della somma è 1/2.
A me è piaciuto molto questo articolo: Luca Lussardi, Sommare le serie non convergenti: istruzioni per l’uso, Matematicamente.it, Magazine Numero 23 - Settembre 2014
3 MARZO 2018
Nei seguenti schemi si chiede di trovare 4 punti che siano i vertici di un dato quadrilatero e disegnarlo.
Seguono alcuni esercizi tratti da http://inabapuzzle.com/study/zukei_q.pdf di Inaba Naoki.
Ma la domanda è: se vuoi creare uno di questi puzzles, qual è la strategia corretta per avere la sicurezza che la soluzione sia unica?
Un'altra domanda potrebbe essere: quanti punti al massimo si possono segnare in una griglia 5x5 affinchè ci sia un solo quadrato (o rombo o rettangolo, etc.)?
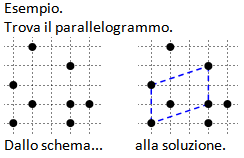
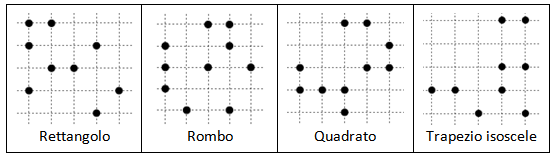
Una soluzione parziale è data da Max Goldstein che ha creato uno Zukei Puzzle Solver online (https://bl.ocks.org/mgold/2ef3afcedd3b41cf355290e7daa7e42c).
Genera sttutture casuali di punti e trova tutti i parallelogrammi, rettangoli, quadrati, rombi che si possono formare con i punti della struttura. Ogni tanto si trovano strutture con una soluzione unica.
Un problema simile (per i rettangoli) è stato trattato nel Forum, vedi Ordine nel caos, grazie gnugnu!
2 FEBBRAIO 2018
La seconda pallina.
In un sacchetto ci sono due palline colorate (i colori possibili sono soltanto bianco e nero).
Se ne pesca una ed è bianca.
Qual è la probabilità che anche l'altra sia bianca?
Generalizzazione.
Sappiamo che in un sacchetto ci sono soltanto palline bianche e palline nere.
Non sappiamo quante sono le palline.
Dal sacchetto estraiamo n palline, una di seguito all'altra, e sono tutte bianche.
Qual è la probabilità che anche la prossima pallina estratta sia bianca?
Indagini.
Furio Honsell, L'algoritmo del parcheggio, Mondadori, 2007.
Kai Lai Chung, Chance & choice memorabilia, World Scientific Publishing Company, 2004. Il primo capitolo del libro si intitola Will the Sun Rise Again? ed è una dimostrazione della regola di successione di Laplace usando il modello dell'urna e delle palline bianche e nere.
Questo problema è stato posto e risolto anche nel Forum, vedi Semplici probabilita ancora piu semplici, grazie Panurgo!
1 GENNAIO 2018
Cari amici, auguro a tutti voi un anno pieno di pace, bene e di ogni cosa bella che desiderate! Assieme all'augurio, vi propongo la tradizionale sfida di inizio anno.
Vedete queste quattro forme?
Stampatele su un cartoncino e ritagliatele. Le parti bianche dentro le forme sono fori da ritagliare. Anche la linea interna nella terza forma è da ritagliare.
Un quadretto della griglia tratteggiata dovrebbe misurare almeno 4x4 cm.
Qual è la sfida? Dovete riuscire a piegare ciascuna forma in modo da costruire la superficie di un cubo il cui lato abbia la stessa lunghezza dei quadrati nelle forme.
Sono ammesse piegature solo lungo le linee della griglia o le diagonali dei quadrati.
Con la prima forma si può costruire un cubo senza sovrapposizioni.
Con le altre forme invece ci sono delle sovrapposizioni.
Fonti: Oswin Aichholzer e altri, Folding Polyominoes into (Poly)Cubes (https://arxiv.org/abs/1712.09317v1) e un post di David Eppstein.
1 GENNAIO 2016
Cari amici, BASE Cinque ha bisogno di riposare un po'.
Per un periodo imprecisato di tempo non inserirò nuovi articoli.
Il sito tuttavia rimane attivo e tutti i suoi contenuti sono raggiungibili consultando l'archivio o il motore di ricerca interno.
Se avete un problema interessante o divertente, non esitate: inviatelo al forum.
Pace e bene a tutti!
Pace e bene a tutti!
Gianfranco Bo
Data creazione: gennaio 2019
Ultimo aggiornamento: gennaio 2019
xhtml 1.1
Sito Web realizzato da Gianfranco Bo