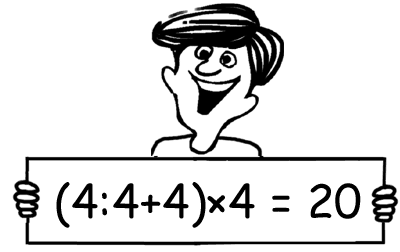
[BASE Cinque - Appunti di Matematica ricreativa]
Scheda PDF dei primi due esercizi.
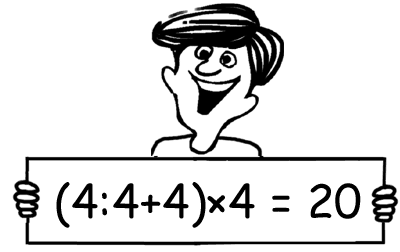
Roberto ha dimostrato come si possono usare quattro 4, le operazioni aritmetiche e le parentesi per ottenere 20.
Utilizzando quattro 4, i segni delle quattro operazioni ed eventualmente le parentesi, sei capace di ottenere tutti i numeri interi da 0 a 10?
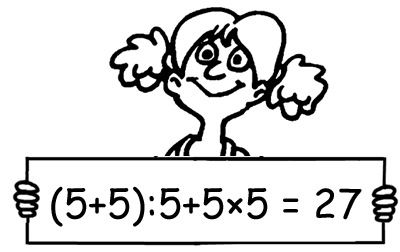
Giulia ha dimostrato come si possono usare cinque 5, le operazioni aritmetiche e le parentesi per ottenere 27.
Utilizzando cinque 5, i segni delle quattro operazioni ed eventualmente le parentesi, sei capace di ottenere tutti i numeri interi da 0 a 10?
Harry dice a Edmund: "Io sono capace di sistemare quattro 1 e alcune
operazioni aritmetiche in modo da ottenere esattamente 12."
Tu sei capace?
Nicolas Pike, A New and Complete System of Arithmetic, composed for the Use of the Citizens of the United States, 1788.
Jack dice a suo fratello Harry: "Io sono capace di sistemare quattro 3 in
modo da ottenere esattamente 34."
Tu sei capace di fare altrettanto?
Thomas Dilworth, Schoolmaster's Assistant, 1743.
Utilizzando quattro 3 e le operazioni aritmetiche ottenere i seguenti numeri:
1/243
1/27
1/3
3
27
243
Esprimere 6,5 con quattro 5
Esprimere 100 con quattro 9.
Mettere assieme tre 6 in modo da ottenere 7.
Thomas Rayner Dawson, nel 1916, fu (forse) il primo a porre il problema dei quattro quattro in termini più generali.
E' possibile, utilizzando quattro R e le operazioni/funzioni aritmetiche, esprimere i numeri interi da 0 a 10?
R indica un numero intero positivo.
Sono ammesse le quattro operazioni, i radicali, l'elevamento a potenza, il fattoriale, il punto decimale.
Questo problema è spostato nella pagina dedicata: Il problema delle quattro R
Esprimere tutte le cifre del sistema decimale utilizzando tre 3.
Come operazioni sono ammesse l'elevamento a potenza, l'estrazione di radice e il
fattoriale.
Inserire opportunamente dei segni di operazioni o funzioni matematiche in
modo da ottenere sempre 6.
1 1 1 = 6
2 2 2 = 6
3 3 3 = 6
4 4 4 = 6
5 5 5 = 6
6 6 6 = 6
7 7 7 = 6
8 8 8 = 6
9 9 9 = 6
Inserire segni matematici noti nella sequenza:
0 1 2 3 4 5 6 7 8 9
in modo da ottenere 100
Inserire segni matematici noti nella sequenza:
9 8 7 6 5 4 3 2 1 0
in modo da ottenere 100
Con le nove cifre, da 1 a 9, disposte sia in ordine crescente che in ordine
decrescente si può ottenere 100. Ma si può fare di più.
Ricordate quanto valgono pi-greco, "e" e la radice quadrata di 2?
pi = 3,14159265359...
e = 2,718281828459...
√2 = 1,414213562373...
Si tratta di tre numeri irrazionali, perciò non potranno mai essere ottenuti a
partire dai numeri interi e dalle quattro operazioni.
Però ci si può avvicinare.
Ecco il problema: utilizzando i numeri da 0 a 9 esattamente una volta, le
operazioni aritmetiche +, -, x, /, le parentesi ( ) e la virgola decimale,
scrivere una espressione il cui risultato sia il più vicino possibile al numero
pi greco.
Stesso esercizio per i numero "e" e la radice quadrata di 2.
Utilizzando soltanto monete da 50 centesimi, 20 centesimi e 5 centesimi è
possibile formare 2 euro con 20 monete?
E 3 Euro?
E 5 euro?
Per farla più facile: Pierino ha a disposizione tre scatole: la prima contiene
100 monete da 500 lire, la seconda contiene 100 monete da 200 lire e la terza
contiene 100 monete da 50 lire. Pierino deve comporre 2000 lire utilizzando
esattamente 20 monete prese dalle tre scatole.
Riuscirà nell'impresa?
Riuscirà a comporre 3000 con 20 monete?
E a comporre 5000 lire?
Inserisci negli spazi fra le cifre il segno opportuno di operazione aritmetica in modo che il risultato di ciascuna riga sia 1.
E' permesso usare le parentesi.
Esempio: (1 + 2) : 3 = 1
1 2 3 4 = 1
1 2 3 4 5 = 1
1 2 3 4 5 6 = 1
1 2 3 4 5 6 7 = 1
1 2 3 4 5 6 7 8 = 1
1 2 3 4 5 6 7 8 9 = 1
Esprimete tutti i numeri da 1 a 100 ed oltre... utilizzando quattro 4 e le regole ammesse nei newsgroups per risolvere questo tipo di problemi.
The Year Game (http://mathforum.org/yeargames) è una sfida posta ogni anno sul Math Forum (https://www.nctm.org/mathforum).
Bisogna esprimere i numeri da 1 a 100 usando le cifre dell'anno in corso e le comuni operazioni/funzioni aritmetiche.
Our rules: use the digits in the year 2019 and the operations +, -, x, : , ^ (raised to a power), sqrt (square root), and ! (factorial), along with grouping symbols, to write expressions for the counting numbers 1 through 100. This year we will also allow the use of decimal points and double-digit numbers.
Chiunque può partecipare.
Esprimere qualsiasi numero, intero e positivo, usando solo tre 2 e segni matematici.
In questo caso è ammesso l'uso dei logaritmi.
Usando i numeri 3, 3, 8, 8, alcune fra le quattro operazioni aritmetiche +, -, ×, : e le parentesi, sei capace di ottenere 24?
Nelle figure vedi come Giulia e Roberto hanno ottenuto due numeri vicini a 24.
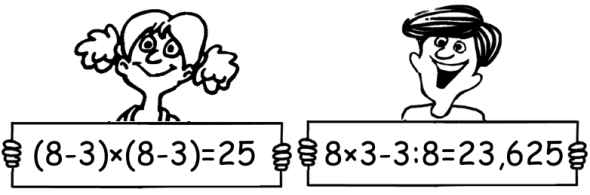
---
Precisazioni:
a) devi usare due volte 3 e due volte 8;
b) puoi scegliere fra le quattro operazioni quelle che ti servono;
c) puoi usare le parentesi;
d) NON puoi usare trucchi del tipo unire i numeri (es. 8 e 3 per ottenere 83) né inserire la virgola decimale né usare radici, fattoriali e così via.
1. I quattro 4
0 = 4 + 4 - 4 - 4
1 = 44/44
2 = 4/4 + 4/4
3 = (4 + 4 + 4)/4
4 = (4 - 4) x 4 + 4
5 = (4 x 4 + 4)/4
6 = (4 + 4)/4 + 4
7 = 4 + 4 - 4/4
8 = 4 + 4 + 4 - 4
9 = 4 + 4 + 4/4
2. I cinque 5
0 = (5 + 5 - 5 - 5) x 5
1 = (5 + 5 x 5)/5 - 5
2 = 5 - (5 + 5 + 5)/5
3 = 5 - 5/5 - 5/5
4 = 5 - 55/55
5 = 5 - 5 + 5 - 5 + 5
6 = 5 + 55/55
7 = 5 + 5/5 + 5/5
8 = 5 +(5 + 5 + 5)/5
9 = (5 x 5 - 5)/5 + 5
3. I quattro 1
1 x 1 + 11 = 12
4. I quattro 3
3/3 + 33 = 34
5. Ancora i quattro 3
3-3 : 3 : 3 = 1/243
(3/3)/33 = 1/27
33-3/3 = 1/3
(3 + 3 + 3)/3 = 3
3 - 3 + 33 = 27
3 x 3 x 3 x 33 = 243
Un particolare ringraziamento a Fausto Belardi per la seguente soluzione.
1/243 = 3^(3/3-3!)
1/27 = 3^-(3/3*3)
1/3 = 3^-(3^(3-3))
3 = 3*3^(3-3) oppure rad cubica (3*3*3)
27 = 3^(3/3*3)
243 = 3^(3!-3/3)
6. I quattro 5
5,5 + 5/5 = 6,5
7. I quattro 9
99 + 9/9
8. I tre 6
6 + 6/6
9. Esprimere i numeri interi da 0 a 10 utilizzando quattro R
Questo problema è spostato in nella pagina dedicata: Il problema delle quattro R
10. I tre 3
0 = 3! - 3 - 3
1 = 3!/(3 + 3)
2 = 3 - 3/3
3 = 3 - 3 + 3
4 = 3 + 3/3
5 = 3! - 3/3
6 = 3! + 3 - 3
7 = 3! + 3/3
8 = 3! + 3!/3
9 = 3 + 3 + 3
11. Sempre e soltanto 6
(1 + 1 + 1)! = 6
2 + 2 + 2 = 6
3! + 3 - 3 = 6
(4 - 4/4)! = 6
5 + 5/5 = 6
6 + 6 - 6 = 6
7- 7/7 = 6
((radq(8 + 8))!/8)! = 6
9 - 9 + (radq(9))! = 6
12. Le nove cifre danno 100
0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 x 9
13. Le nove cifre danno ancora 100
9 x 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0
14. Avvicinarsi a Pi greco
Ad esempio:
1,6924/0,5387 = 3,14163...
Non c'è male, è pi greco a meno di un millesimo. Ma la seguente è mille volte
più precisa.
(347+8)/(5+12+96) = 355/113 = 3,14159292...
15. Formare 2 euro con 20 monete (o 2000 lire)
Un particolare ringraziamento a Giorgio Tumelero, autore della seguente risoluzione.
Sinteticamente possiamo scrivere:
500x + 200y + 50z = 2000 (equazione 1)
1x + 1y + 1z = 20 (equazione 2)
Moltiplichiamo l'equazione 2 per -50 e sommiamola all'equazione 1, otteniamo:
450x + 150y = 1000
ovvero, dividendo tutto per 50:
9x + 3y = 20 (equazione 3)
ovvero: y = 20/3 - 3x
Ma per qualsiasi valore intero di x avremo sempre un valore frazionario di y (e
quindi di z); quindi il problema e' irrisolvibile.
Lo stesso se cerchiamo di ottenere 3000 o 5000 lire. Con 4000 lire invece
avremmo che l'equazione 3 diventa:
9x + 3y = 60 ovvero, semplificando:
3x + y = 20 (equazione 3')
ovvero: y = 20 - 3x
da cui si ottengono le sette soluzioni (x, y, z) = (0,20,0), (1,17,2), (2,14,4),
ecc.
Uno studioso delle frazioni continue avrebbe subito detto:
"L'equazione diofantea ax + by = c ha soluzioni se e solo se il coefficiente c
e' divisibile per il M.C.D. dei coefficienti a e b. Quindi l'equazione 3 e'
irrisolvibile."
16. Sempre uno
1 x 2 + 3 - 4 = 1
1 - 2 + 3 + 4 - 5 = 1
1 x [2 - (3 - 4) x (5 - 6)] = 1
(1 + 2) : [3 x (4 - 5) x (6 - 7)] = 1
1 x [2+ (3 - 4) x (5 - 6) x (7 - 8)] = 1
1 x (2 - 3) x (4 - 5) x (6 - 7) x (8 - 9) = 1
17. I record dei 4 4
Nei newsgroup di matematica ricreativa si è formato a poco a poco un sistema di regole ammesse per risolvere problemi di questo tipo.
Sono ammesse le seguenti operazioni e funzioni matematiche:
+, -, *, /, estrazione di radice quadrata, elevamento a potenza, fattoriale)
E' inoltre possibile utilizzare le notazioni:
Non è ammesso l'uso del logaritmo perché in tal caso sarebbe possibile ottenere qualsiasi numero e allora non ci sarebbe più da divertirsi!
Perché con il logaritmo, assieme alla radice quadrata, si può esprimere qualunque numero intero con 4 4?
Ecco perché:
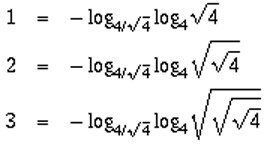
In pratica le espressioni sono del tipo:
- log2 [ log4
(4(1/2)n) ] =
- log2 [ (1/2)n) log4 4 ] =
- log2 (1/2)n =
- n log2 (1/2) =
n
Ed ecco i risultati da 1 a 200 e oltre!
Vi ricordo che:
sqrt(4) =
√4 = 2
4! = 24
.4 = 4/10
.4~ = .(4) = .44444444...(periodico) = 4/9
| Numero | Espressione con quattro 4 |
| 0 | 4 - 4 + 4 - 4 |
| 1 | (4/4) / (4/4) |
| 2 | 4/4 + 4/4 |
| 3 | (4+4+4) / 4 |
| 4 | [ (4/4) ^4 ] * 4 |
| 5 | [ 4*4 +4 ] / 4 |
| 6 | [ (4+4) /4 ] +4 |
| 7 | 4 + 4 - (4/4) |
| 8 | 4*4 - 4 - 4 |
| 9 | 4/4 + 4 + 4 |
| 10 | 4 + 4 + 4 - sqrt(4) |
| 11 | 44 / (sqrt(4) + sqrt(4)) |
| 12 | 4 + 4 + sqrt(4) + sqrt(4) |
| 13 | 4!/(sqrt(4)) + 4/4 |
| 14 | 4+4+4 + sqrt(4) |
| 15 | (44/4)+4 |
| 16 | 4*4*4 / 4 |
| 17 | 4*4 + 4/4 |
| 18 | 4*4 + 4 / sqrt(4) |
| 19 | 4! - 4 - 4/4 |
| 20 | 4 * 4 + sqrt(4) + sqrt(4) |
| 21 | 4! - 4 + 4/4 |
| 22 | 4! - (4! / 4 - 4) |
| 23 | 4! - 4^(4-4) |
| 24 | 4 * [ 4 + 4/sqrt(4) ] |
| 25 | 4! + 4^(4-4) |
| 26 | 4! + (4! / 4 + 4) |
| 27 | 4! + 4 - 4/4 |
| 28 | 4! + 4 * (4/4) |
| 29 | 4! + 4 + 4/4 |
| 30 | (4 + 4/4)! / 4 |
| 31 | (4! + 4)/4 +4! |
| 32 | 4*4 + 4*4 |
| 33 | (4 - .4)/.4 + 4! |
| 34 | 4*4 * sqrt(4) + sqrt(4) |
| 35 | 4! + 44/4 |
| 36 | 4*4 * sqrt(4) + 4 |
| 37 | 4! + (4! + sqrt(4)) / sqrt(4) |
| 38 | 44 - 4 - sqrt(4) |
| 39 | 4! + 4! - 4/.4~ |
| 40 | 44 - sqrt(4) - sqrt(4) |
| 41 | (4*4 + .4) / .4 |
| 42 | 44 - 4/sqrt(4) |
| 43 | 44 - 4/4 |
| 44 | 44 + 4 - 4 |
| 45 | 44 + 4/4 |
| 46 | 44 + 4/sqrt(4) |
| 47 | 4! + 4! - 4/4 |
| 48 | 44 + sqrt(4) + sqrt(4) |
| 49 | 4! + 4! + 4/4 |
| 50 | 44 + 4! / 4 |
| 51 | (4! - 4 + .4) / .4 |
| 52 | 44 + 4 + 4 |
| 53 | 44 + 4 / .4~ |
| 54 | 4! + 4! + (4! / 4) |
| 55 | {4! - [ 4 / sqrt(4) ] } / .4 |
| 56 | 44 + 4! / sqrt(4) |
| 57 | 4! + 4! + 4/.4~ |
| 58 | 4! + 4! + 4/.4 |
| 59 | 4!/.4 - 4/4 |
| 60 | 44 + 4 * 4 |
| 61 | 4!/.4 + 4/4 |
| 62 | (4 + 4) ^ (sqrt(4)) - sqrt(4) |
| 63 | (4! + sqrt4) / .4 - sqrt(4) |
| 64 | 4 * 4 * sqrt(4) * sqrt(4) |
| 65 | (4^4 +4) / 4 |
| 66 | (4 + 4) ^ [sqrt(4)] + sqrt(4) |
| 67 | [4! + sqrt(4)] / .4 + sqrt(4) |
| 68 | (4 + 4) ^ (sqrt(4)) + 4 |
| 69 | (4!+4-.4)/.4 |
| 70 | 44 + 4! + sqrt(4) |
| 71 | (4 + 4! + .4) / .4 |
| 72 | [ (4! / 4) ^ sqrt(4) ] * sqrt(4) |
| 73 | [4! * sqrt(4) + sqrt(.4~)] / sqrt(.4~) |
| 74 | 4! + 4! + 4! + sqrt(4) |
| 75 | (4! + sqrt(4) + 4) / .4 |
| 76 | 4!*4 - 4! + 4 |
| 77 | (4/.4~) ^ sqrt(4) - 4 |
| 78 | sqrt(4 / .4~) * [4! + sqrt(4)] |
| 79 | (4/.4~) ^ (sqrt(4)) - sqrt(4) |
| 80 | 4! * 4 - 4*4 |
| 81 | (4/.4~) * (4/.4~) |
| 82 | (4! / .4) + 4! - sqrt(4) |
| 83 | (4/.4~) ^ (sqrt(4)) + sqrt(4) |
| 84 | 4! * 4 - 4! / sqrt(4) |
| 85 | (4/.4~) ^ (sqrt(4)) + 4 |
| 86 | 4!*4 - 4/.4 |
| 87 | 4! * 4 - 4/.4~ |
| 88 | 4! * 4 - 4 - 4 |
| 89 | 4! + [4! + sqrt(4)]/.4 |
| 90 | 4! * 4 - 4! / 4 |
| 91 | 4 * 4! - (sqrt(4) / .4) |
| 92 | 4! * 4 - sqrt(4*4) |
| 93 | 4 * 4! - [ sqrt(4) / sqrt (.4~) ] |
| 94 | 4! * 4 - 4/sqrt(4) |
| 95 | 4! * 4 - 4/4 |
| 96 | 4! * 4 + 4 - 4 |
| 97 | 4! * 4 + 4/4 |
| 98 | 4! * 4 + 4/sqrt(4) |
| 99 | [4!*sqrt(4)-4] / .4~ |
| 100 | 4! * 4 + sqrt(4*4) |
| 101 | 44/.4~ + sqrt(4) |
| 102 | 4! * 4 - 4! / 4 |
| 103 | (44 / .4~) + 4 |
| 104 | 4*4!+4+4 |
| 105 | 4! * 4 + 4/.4~ |
| 106 | [4!+sqrt(4)] *4 +sqrt(4); |
| 107 | (4! + 4! - .4~) / .4~ |
| 108 | 4! * 4 + 4! / sqrt(4) |
| 109 | (4! + 4! + 4~) / .4~ |
| 110 | (4! + 4! - 4) / .4 |
| 111 | 444 / 4 |
| 112 | 4! * 4 + 4*4 |
| 113 | |
| 114 | 44/.4 + 4 |
| 115 | [4! + 4! - sqrt(4)] / .4 |
| 116 | (4+ 4/4)! - 4 |
| 117 | (4! + 4! + 4) / .4~ |
| 118 | (4+ 4/4)! - sqrt(4) |
| 119 | (4! + 4! -.4) / .4 |
| 120 | (4! * 4!) / 4 - 4! |
| 121 | (4! + 4! + .4) / .4 |
| 122 | (4+ 4/4)! + sqrt(4) |
| 123 | (44 / .4~) + 4! |
| 124 | (4+ 4/4)! + 4 |
| 125 | [4! * sqrt(4) + sqrt(4)] / .4 |
| 126 | (4^4) / sqrt(4) - sqrt(4) |
| 127 | [ 4^4 - sqrt(4) ] / sqrt(4) |
| 128 | (4^4) * sqrt(4) /4 |
| 129 | [4^4 + sqrt(4)] / sqrt(4) |
| 130 | (4^4) / sqrt(4) + sqrt(4) |
| 131 | 4! / (.4 * .4~) - 4 |
| 132 | (4^4) / sqrt(4) + 4 |
| 133 | 4! / (.4~*.4) - sqrt(4) |
| 134 | (44 / .4) + 4! |
| 135 | 4! / [(sqrt(.4 * .4)) * .4~] |
| 136 | (4 / .4 + 4!) * 4 |
| 137 | 4! / (.4~*.4) + sqrt(4) |
| 138 | (4!^sqrt(4) - 4!) / 4 |
| 139 | 4! / (.4*.4~) + 4 |
| 140 | 4! * 4 + 44 |
| 141 | [4*4! - sqrt(4)] / sqrt(.4~) |
| 142 | 4! * 4! /4 - sqrt(4) |
| 143 | (4!^sqrt(4) - 4) / 4 |
| 144 | [ 4!^(4 / sqrt(4)) ] / 4 |
| 145 | (4!^sqrt(4) + 4) / 4 |
| 146 | [4!/(.4 * .4)] - 4 |
| 147 | [4*4! + sqrt(4) ] / sqrt(.4~) |
| 148 | (4*4!) / sqrt(.4~) + 4 |
| 149 | ( 4!/.4 - .4 ) / .4 |
| 150 | (4!*4!+4!)/4 |
| 151 | [(4!/.4) + .4] / .4 |
| 152 | [4! / (.4 * .4)] + sqrt(4) |
| 153 | (44 + 4!) / .4~ |
| 154 | 4! / (.4 * .4) + 4 |
| 155 | [(4!/.4) + sqrt(4)] / .4 |
| 156 | 4! * [4! + sqrt(4)] / 4 |
| 157 | |
| 158 | sqrt(sqrt(sqrt(4^(4!)))) / .4 - sqrt(4) |
| 159 | 4!/(.4~ * .4) + 4! |
| 160 | 4 * 4 * 4 / .4 |
| 161 | [sqrt(sqrt(sqrt(4^(4!)))) + .4] / .4 |
| 162 | (4! + 4! + 4!) / .4~ |
| 163 | |
| 164 | sqrt(sqrt(sqrt(4^(4!)))) / .4 + 4 |
| 165 | 44 / [sqrt(.4~) * .4] |
| 166 | |
| 167 | |
| 168 | [44 - sqrt(4)] * 4 |
| 169 | { [ 4! + sqrt(4) ] / sqrt(4) } ^ sqrt(4) |
| 170 | (4! + 44) / .4~ |
| 171 | |
| 172 | 44 * 4 - 4~ |
| 173 | |
| 174 | 44 * 4 - sqrt(4) |
| 175 | (4!+4) / (.4*.4) |
| 176 | 44 * sqrt(4) * sqrt(4) |
| 177 | {sqrt(4)/.4]! - sqrt(4)} / sqrt(.4~) |
| 178 | 44 * 4 + sqrt(4) |
| 179 | [ (4!/4)! - 4] / 4 |
| 180 | (4! - 4) * 4 / .4~ |
| 181 | [(4!/4)! + 4] / 4 |
| 182 | [(4!/4)!] / 4 + sqrt(4) |
| 183 | ((sqrt(4)/.4)! + sqrt(4)) / sqrt(.4~) |
| 184 | [44 + sqrt(4) ] * 4 |
| 185 | |
| 186 | |
| 187 | |
| 188 | 4! * sqrt(4) * 4 - 4 |
| 189 | (4! + 4!/ .4) / .4~ |
| 190 | 4! * sqrt(4) * 4 - sqrt(4) |
| 191 | |
| 192 | (44+4) * 4 |
| 193 | |
| 194 | 4! * sqrt(4) * 4 + sqrt(4) |
| 195 | (4!/.4~ + 4!) / .4 |
| 196 | 4! * sqrt(4) * 4 + 4 |
| 197 | |
| 198 | 44 * sqrt(4) / .4~ |
| 199 | |
| 200 | (4!*4 + 4) * sqrt(4) |
| 201 | |
| 202 | 4^4 - 4 / .4~ |
| 203 | |
| 204 | (4!/4)! / 4 + 4! |
| 205 | |
| 206 | |
| 207 | (4*4! - 4) / .4~ |
| 208 | 4^4 - 4!*sqrt(4) |
| 210 | 4 * [4! - sqrt(.4~)] / .4~ |
| 212 | 4^4 - 44 |
| 214 | 4 * 4! / .4~ - sqrt(4) |
| 215 | (4 * 4! - .4~) / .4~ |
| 216 | 4 * (4! + 4!) + 4! |
| 217 | (4 * 4! + .4~) / .4~ |
| 218 | 4 * 4! / .4~ + sqrt(4) |
| 220 | 44 * sqrt(4) / .4 |
| 222 | 444 / sqrt(4) |
| 224 | (4! + 4) * (4 + 4) |
| 225 | (4 * 4! + 4) / .4~ |
| 228 | 4^4 - 4! - 4 |
| 230 | (4 * 4! - 4) / .4 |
| 236 | [ (4 * 4!) / .4] - 4 |
| 241 | (4! * 4 + .4) / .4 |
| 242 | 4! / .4~ / .4~ / sqrt(4) |
| 264 | 44 * 4! / 4 |
| 575 | (4^4 - .4~) / .4~ |
| 577 | (4^4 + .4~) / .4~ |
| 639 | (4^4 - .4) / .4 |
| 641 | (4^4 + .4) / .4 |
| 704 | 44 * 4 * 4 |
18. The year game
...
19. Qualunque numero con tre 2

Soluzione inviata da Pietro Vitelli al Forum
20. Il problema 3388
La difficoltà del problema sta nel fatto che bisogna usare un doppio livello nella precedenza fra le operazioni.
8 : (3 - 8 : 3) = 8 : (1/3) = 8 * 3 = 24
E' anche il problema più interessante di questo tipo con i numeri da 1 a 9.
---
Pace e bene a tutti.
GfBo
Data creazione: luglio 2000
Ultimo aggiornamento: maggio 2021
html 5
Sito Web realizzato da Gianfranco Bo