
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Questa pagina è stata realizzata con la collaborazione degli alunni della
Scuola Media di Cogorno, gruppo giochi matematici, classi seconda e terza
media.
Un particolare ringraziamento a Pietro Vitelli per la soluzione degli ultimi 3
esercizi.
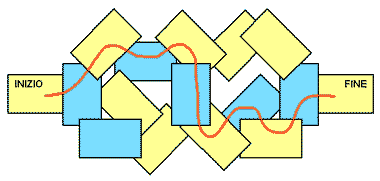
Nella figura vedete 16 carte disposte su un tavolo. Ogni carta
è colorata di giallo oppure di celeste.
Partite dall'INIZIO (carta gialla) e passate sulla carta celeste a contatto con
essa. Poi passate su una carta gialla a contatto con la precedente. Poi passate
su una carta celeste. Continuate così, giallo, celeste, giallo, celeste,
...fino a raggiungere la FINE del percorso (carta gialla).
Potete passare più volte su una stessa carta.

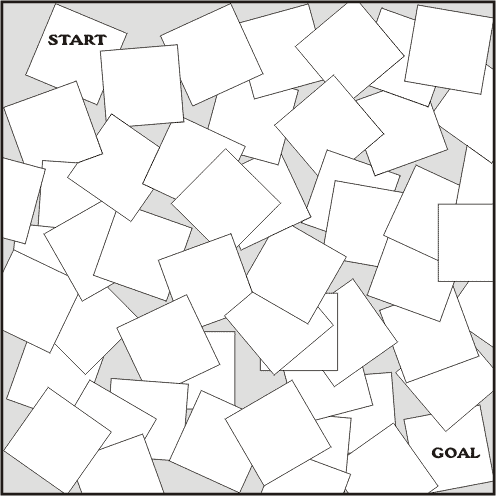
Nella figura vedete 16 carte disposte su un tavolo. Ogni carta
può essere sopra oppure sotto un'altra carta.
Partite dall'INIZIO e SALITE sulla prima carta. Poi SCENDETE su una carta che
sta sotto. Poi SALITE su una carta che sta sopra. Continuate così, andando SU,
GIU', SU, GIU', ...fino a raggiungere la FINE del percorso.
Potete passare più volte su una stessa carta.
Una piccola difficoltà in più: trovate un percorso che attraversi tutte le
carte.

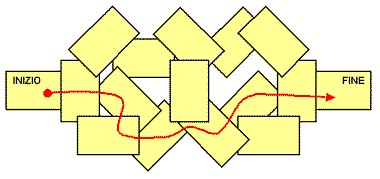
Ripetete lo stesso esercizio con queste 16 carte.
(di Adrian Fisher)

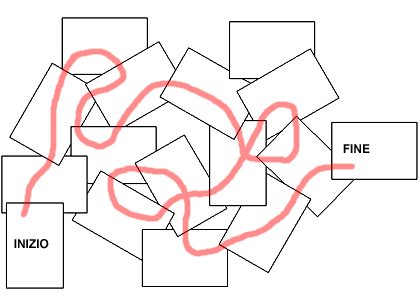
Il seguente esercizio è di Nobuyuki Yoshigahara (1936-2004)
definito da Serhiy Grabarchuk un guru giapponese dei puzzles logico
matematici.
La seguente figura è tratta da:
http://www.ageofpuzzles.com/Masters/NOB/NOB.htm
Per la risposta di questo labirinto, vi rimando al seguente articolo:
Carte sopra, carte sotto di
Nobuyuki Yoshigahara
Gli ultimi tre si chiamano labirinti multistato.
Quando siete SCESI su una carta potete immaginare di essere nello stato BASSO;
in questo stato dovete cercare una carta su cui SALIRE.
Quando siete SALITI su una carta potete immaginare di essere nello stato ALTO;
in questo stato dovete cercare una carta su cui SCENDERE.
Ripassando su una stessa carta potreste trovarvi in due stati diversi, a
seconda della carta da cui siete provenuti.
Il labirinto carte gialle e carte celesti non è multistato perché ogni
carta corrisponde ad un solo stato, determinato dal suo colore.
Nella figura vedete 25 cerchi colorati (A = rosa, B =
giallo, C = celeste), collegati da un reticolo di vie.
Partite dall'INIZIO (cerchio rosa) e passate su un cerchio giallo collegato ad
esso. Poi passate su un cerchio celeste e quindi ancora su un cerchio
giallo.
Continuate ripetendo la sequenza A - B - C - B,... fino a raggiungere la FINE
del percorso (cerchio celeste).
Potete passare più volte su uno stesso cerchio.

Partite dalla casella S (start).
Fate 1 passo in una direzione (nord, sud, est, overst).
Poi 2 passi nella stessa o in un'altra direzione.
Poi 3 passi nella stessa o in un'altra direzione.
Ripetete 1, 2, 3 passi, e così di seguito fino a giungere alla casella F
(finish).
Mentre fate i 2 e i 3 passi, sono eclusi il dietro-front e il cambio di
direzione.

Questo esercizio, ideato da Erich Friedman è simile al
precedente.
Partite dalla casella S (start).
Fate 1 passo in una delle 4 direzioni cardinali (nord, sud, est, ovest).
Poi 2 passi nella stessa o in un'altra delle 4 direzioni cardinali.
Poi 3 passi nella stessa o in un'altra delle 4 direzioni cardinali.
Poi 4 passi nella stessa o in un'altra delle 4 direzioni cardinali.
Poi 5 passi nella stessa o in un'altra delle 4 direzioni cardinali.
Ripetete 1, 2, 3, 4, 5 passi, e così di seguito fino a giungere alla casella F
(finish).

I totali parziali della vostra passeggiata devono sempre
essere dei numeri primi (2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67
71 73 79 83 89 97 101 103 107 109 113 127 131...).
Non sono ammessi dietro-front.
Siete capaci, partendo dallo START, di terminare realizzando un totale di
97?
Esempio: alla partenza trovate un 5. Andare a nord è scorretto perché (5+4=9,
non primo), mentre andare a est (5+2=7) e a sud (5+6=11) sono entrambe
soluzioni accettabili.


Per la risposta di questo labirinto, vi rimando al seguente articolo:
Carte sopra, carte sotto di Nobuyuki Yoshigahara
Il labirinto ABC

Pietro Vitelli
La soluzione minima si ottiene percorrendo 12 quadretti, che equivalgono a:
12 = 1+2+3+1+2+3
Ecco due possibili soluzioni con 12 quadretti:

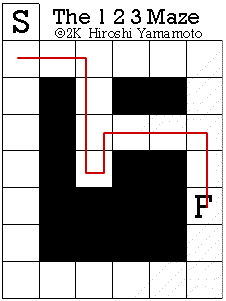
Pietro Vitelli
La soluzione minima si ottiene percorrendo 15 quadretti; equivalenti a:
15 = 1+2+3+4+5
Ecco una possibile soluzione con 15 quadretti:

Pietro Vitelli

Il percorso ci da:
5+2=7+4=11+2=13+4=
17+6=23+8=31+6=
37+4=41+2=43+4=
47+6=53+8=61+6=
67+4=71+2=73+6=
79+4=83+6=89+8=
97,
dove i numeri in rosso sono tutti primi.
.
.
Pace e bene a tutti!
Gianfranco Bo
Data creazione: 2003
Ultimo aggiornamento: aprile 2019
html 4.01
Sito Web realizzato da Gianfranco Bo