[BASE Cinque - Appunti di Matematica ricreativa]

Ordine nel caos

E' vero che il disordine completo è impossibile?

E' vero che un insieme totalmente casuale, purché sufficientemente grande, contiene sicuramente un sottoinsieme che presenta qualche regolarità?

Ebbene sì, è vero, ma al di là di questa banale risposta vi propongo di risolvere alcuni problemi usando ragionamenti matematici. Senza però scomodare la teoria di Ramsey ma utilizzando soltanto il principio dei cassetti.

Problema 1 - Un insieme di 5 numeri interi positivi

Scegliete in modo del tutto casuale 5 numeri interi positivi. Non ci sono limiti alla grandezza dei numeri. Sono ammesse ripetizioni.

Dimostrate che in questo insieme di 5 numeri, comunque siano stati scelti, ce ne sono sicuramente alcuni (da 1 a 5) la cui somma è divisibile per 5.

Soluzione.

Facciamo dapprima un esempio. Scriviamo un insieme di 5 numeri naturali.

{9, 132, 14, 72, 29}

Il metodo inutile

Nessuno dei numeri è divisibile per 5.

Nessuna coppia è divisibile per 5.

Potremmo esaminare pazientemente tutte le terne e le quaterne e la cinquina e alla fine troveremmo per esempio che:

29 + 9 + 72 = 110, divisibile per 5.

Questo metodo di ricerca della soluzione non va bene perché funziona solo in questo caso particolare e non aiuta a trovare un ragionamento generale.

Inoltre, se i numeri, invece di 5 fossero 50, la ricerca di tutte le combinazioni sarebbe decisamente troppo lunga.

Un metodo buono

• Scriviamo i numeri in ordine (non è obbligatorio ma poi vedremo perché è importante)

9, 14, 29, 72, 132

• Scriviamo le seguenti sequenze e le relative somme e osserviamole.

9 = 9

9 + 14 = 23

9 + 14 + 29 =52

9 + 14 + 29 + 72 = 124

9 + 14 + 29 + 72 + 132 = 256

E' un caso davvero sfortunato, nessuna di esse è divisibile per 5.

• Scriviamo allora tutti i risultati in modulo 5, cioè calcoliamo tutti i resti della divisione per 5.

9 = 9 = 4 mod 5

9 + 14 = 23 = 3 mod 5

9 + 14 + 29 =52 = 2 mod 5

9 + 14 + 29 + 72 = 124 = 4 mod 5

9 + 14 + 29 + 72 + 132 = 256 = 1 mod 5

• Osserviamo che ci sono 5 somme distinte ma i resti distinti delle divisioni possono essere soltanto 4, perché abbiamo escluso il resto 0.

• Dunque, per il principio dei cassetti, devono esistere almeno due moduli (resti) uguali. In questo caso sono:

9 + 14 + 29 + 72 = 124 = 4 mod 5

9 = 9 = 4 mod 5

• Per un noto teorema, la differenza fra le due somme è divisibile per 5.

9 + 14 + 29 + 72 - 9 = 14 + 29 + 72 = 115 = 0 mod 5

• E ora viene la conclusione.
  L'insieme di numeri che abbiamo ottenuto {14, 29, 72} è sicuramente un sottoinsieme dell'insieme numerico di partenza {9, 14, 29, 72, 132}

Nota.

Grazie a Pietro Vitelli per aver proposto al Forum di BASE Cinque una soluzione valida di questo problema (http://www.base5forum.it/esercizi-sul-principio-dei-cassetti-n-10-somma-divisibile-per-5-t841.html)

Somma e prodotto di uno o zero termini?

In generale, il problema 1 chiede di dimostrare che: in qualunque insieme di n numeri interi positivi, ce ne sono alcuni la cui somma è divisibile per n.

Aggiungo qui qualche precisazione.

• Con il termine "alcuni", si intende "da 1 a n";

Come è definita la somma di un solo addendo?

E il prodotto di un solo fattore?

E la somma e il prodotto di 0 (zero) termini?

Abbiamo discusso ampiamente l'argomento in questa pagina del Forum, perciò qui riporto soltanto le conclusioni.

• La somma di un solo addendo è uguale all'addendo stesso.
• La somma di zero addendi è uguale a 0 (zero).
• Il prodotto di un solo fattore è uguale al fattore stesso.
• Il prodotto di zero fattori è uguale a 1 (uno)

Generalizziamo il problema precedente al caso di n numeri.

Problema 2 - Sequenza nella sequenza

Scegliete in modo del tutto casuale n numeri interi positivi. Non ci sono limiti alla grandezza dei numeri. Sono ammesse ripetizioni. Dimostrate che in questo insieme di n numeri, comunque siano stati scelti, ce ne sono sicuramente alcuni (da 1 a n) la cui somma è divisibile per n.

Soluzione.

• Indichiamo gli n numeri con le lettere:
  a₁, a₂, a₃, ..., a_n
  e supponiamo che siano in ordine crescente.
• Consideriamo le seguenti somme.
  s₁ = a₁
  s₂ = a₁ + a₂
  s₃ = a₁ + a₂ + a₃
  .
  .
  .
  s_n = a₁ + a₂ + a₃ + ... + a_n
• Se una delle somme è divisibile per n, abbiamo concluso.
• Supponiamo però che nessuna di esse sia divisibile per n.
  Scriviamo allora tutti i risultati in modulo 5, cioè calcoliamo tutti i resti della divisione per n.
• Osserviamo che ci sono n somme distinte ma i resti distinti delle divisioni possono essere soltanto n-1, perché abbiamo escluso il resto 0.
• Dunque, per il principio dei cassetti, devono esistere almeno due moduli (resti) uguali.
  Indichiamoli con s_h e s_k, dove s_h < s_k
• Per un noto teorema, la loro differenza, cioè s_k - s_h è divisibile per 5.
  Cioè:

  a_h+1 + a_h+2 + ... + a_k = 0 mod n

• E ora viene la conclusione.
  L'insieme di numeri che abbiamo ottenuto:
  {a_h+1, a_h+2, ... , a_k}
  è sicuramente un sottoinsieme dell'insieme numerico di partenza:
  {a₁, a₂, a₃, ..., a_n}

Abbiamo dimostrato qualcosa di più di quanto richiesto

In realtà abbiamo dimostrato che:

Problema 3 - Griglia di punti colorati

Considerate una griglia rettangolare formata da 3 × 9 punti.

Ogni punto è colorato di bianco o di nero, in modo del tutto casuale.

Dimostrate che in tale griglia, comunque siano colorati i punti, esiste un rettangolo che ha i vertici dello stesso colore.

Si assume che i lati del rettangolo sono paralleli ai lati della griglia

Quali sono le dimensioni minime, a × b, della griglia affinchè tale rettangolo esista?

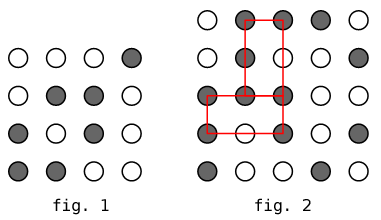
In figura 1 si vede una griglia di 4×4 punti snza nessun rettangolo con i vertici dello stesso colore.
In figura 2 c'è una griglia 5×5 con due rettangoli evidenziati in rosso.

Pace e bene a tutti!

Gianfranco Bo

Data creazione: settembre 2014

Ultimo aggiornamento: ottobre 2014

xhtml 1.1

Sito Web realizzato da Gianfranco Bo