[BASE Cinque - Appunti di Matematica ricreativa]
Il teorema di Tolomeo è ricordato alcune volte su BASE Cinque, per esempio nelle pagine:
E' un teorema semplice, potente e bello a cui purtroppo si dà poca importanza a scuola. Merita una maggiore attenzione.
Allora gli dedico una pagina, prendendo spunto da un problema postato al Forum da Panurgo.
Esagono in un cerchio.
Un esagono con i lati di lunghezza 2, 7, 2, 11, 7, 11 è inscritto in un cerchio di raggio...?
Ricordiamo che: quadrilatero ciclico = quadrilatero inscritto in una circonferenza.
---
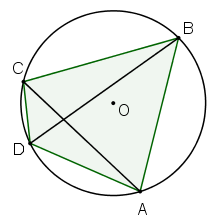
Teorema di Tolomeo. In un quadrilatero ciclico, il prodotto delle misure delle diagonali è uguale alla somma dei prodotti delle misure dei lati opposti.

AC · BD = AD · CB + DC · AB
---
Se il quadrilatero è inscritto in una semicirconferenza, allora si formano due triangoli rettangoli. Una proprietà in più che potrebbe essere utile.
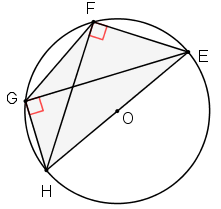
Se il quarilatero è un rettangolo, scopriamo che il teorema di Tolomeo è una generalizzazione del teorema di Pitagora.
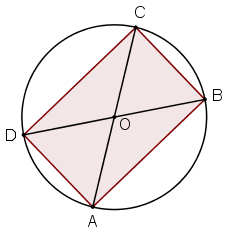
AC · BD = AD · BC + CD · AB
Sostituiamo, tenendo conto delle seguenti uguaglianze:
AC2 = AD2 + CD2
Dimostrazione del teorema di Tolomeo.
Scegliere sulla diagonale AC un punto E tale che l'angolo AED sia uguale all'angolo BCD.
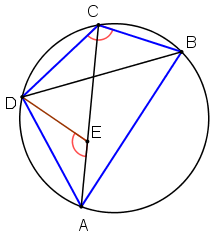
Osservare.
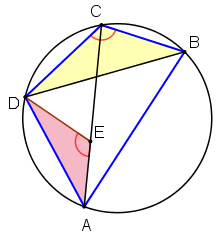
I triangoli AED e BCD sono simili.
Quindi: AE · BD = AD · BC
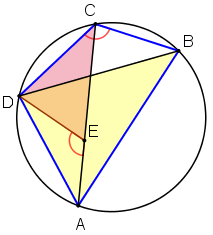
I triangoli DAB e DEC sono simili.
Quindi: CE · BD = CD · AB
Concludere.
Sommando le due uguaglianze:
AE · BD = AD · BC +
CE · BD = CD · AB =
----------------------------
AE · BD + CE · BD = AD · BC + CD · AB =
(AE + CE) · BD = AD · BC + CD · AB =
AC · BD = AD · BC + CD · AB
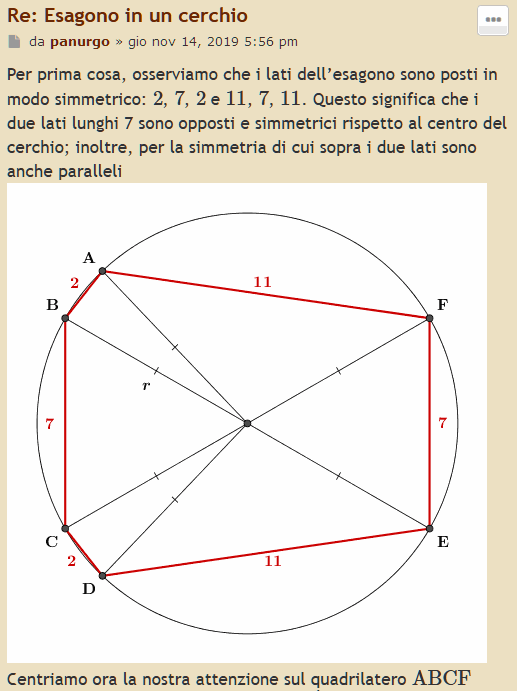
Esagono in un cerchio.
Un esagono con i lati di lunghezza 2, 7, 2, 11, 7, 11 è inscritto in un cerchio di raggio...?
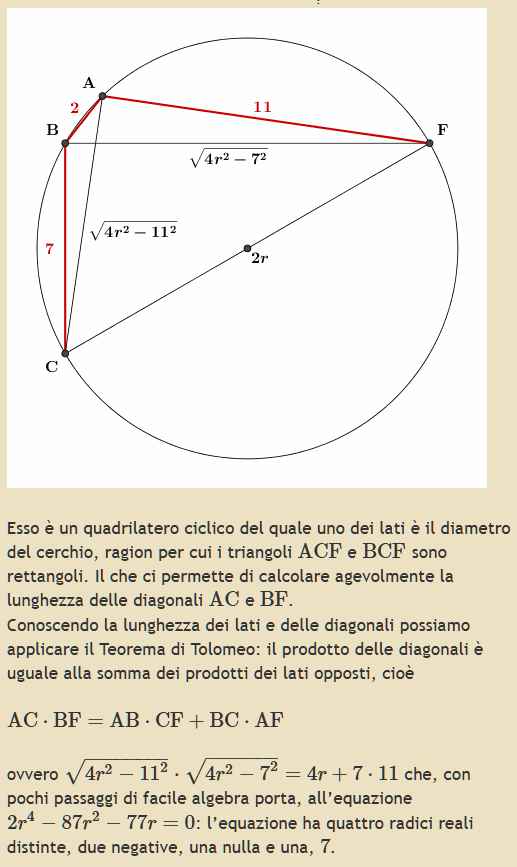
Il problema si può risolvere usando la trigonometria, ma la soluzione geometrica che usa il teorema di Tolomeo è decisamente più carina.
Data creazione: 2019
Ultimo aggiornamento: 2019
xhtml 1.1
Sito Web realizzato da Gianfranco Bo