[BASE Cinque - Appunti di Matematica ricreativa]

Zio Hamming ti sgamma

Da un gioco di divinazione binaria al codice di Hamming

Sette domande, una menzogna

Come si può indovinare un numero pensato, ponemdo il numero minimo di domande che hanno risposte del tipo sì/no e correggendo un errore o una menzogna?

La seguente attività è tratta da Sette domande, una menzogna..., di Andrea Caranti, Matteo Zendron, Maurizio Marinelli, Matteo Corazza, Francesco Prantil, Lorenzo Valdan, Dipartimento di Matematica e Corso di Laurea in Matematica, Facoltà di Scienze Matematiche, Fisiche e Naturali Università di Trento.(http://www-math.science.unitn.it/~caranti/).

Pensate un numero da 0 a 15 compresi.

• Io vi farò sette domande su questo numero.
• Le domande ammettono solo risposta sí oppure no.
• Potete rispondere sempre correttamente, oppure mentire una volta sola.
• Io mi impegno a indovinare comunque il numero.

Le domande sono:

1. È maggiore di 7?
2. È uno fra 4; 5; 6; 7; 12; 13; 14; 15?
3. È uno fra 2; 3; 6; 7; 10; 11; 14; 15?
4. È dispari?
5. È uno fra 2; 3; 4; 5; 8; 9; 14; 15?
6. È uno fra 1; 2; 4; 7; 9; 10; 12; 15?
7. È uno fra 1; 3; 4; 6; 8; 10; 13; 15?
   

Le domande 1, 2, 3, 4 chiedono i quattro bit che esprimono in base 2 il numero pensato (vedi la pagina Divinazione binaria).

Le domande 5, 6, 7 servono a individuare la menzogna, ovvero l’errore.

I codici a correzione d’errore servono proprio a correggere gli errori che inevitabilmente si verificano nel corso di una trasmissione di dati.

Ai dati da trasmettere (in questo caso, le quattro domande originali, che già da sole determinerebbero il numero) vengono aggiunti dati che sarebbero ridondanti, ma che permettono di rivelare o magari di correggere uno o più errori.

Un gioco geometrico rivela l'errore

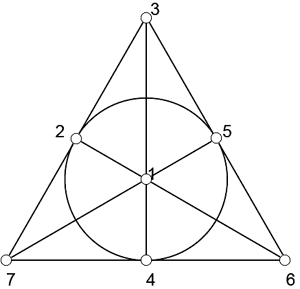
L'errore si può scoprire con un piccolo gioco geometrico. Si disegna uno schema come quello della figura qui sotto. Ogni punto rappresenta la risposta ad una domanda. I punti sono numerati secondo lo stesso ordine delle domande.

Mentre voi rispondete alle domande, io segno sul piano un punto nero per ogni “sí”, e un punto bianco per ogni “no”.

Se non avete mentito ci sono 4 possibilità:

• Ci sono tre punti neri e quattro bianchi, e i tre punti neri stanno su una retta.
• Ci sono tre punti bianchi e quattro neri, e i tre punti bianchi stanno su una retta.
• Tutti i punti sono neri. (Quando il numero è 15.)
• Tutti i punti sono bianchi. (Quando il numero è 0.)
  

Se avete mentito (una volta), c’è un unico modo di cambiare un punto in modo da ricondursi a una di queste situazioni.

Questo punto corrisponde alla risposta inesatta.

Per "indovinare" il numero pensato, si guardano i colori dei punti 1, 2, 3, 4. Ad ogni punto corrisponde un bit:

• bianco = 0
• nero = 1
  

Facciamo qualche prova.

1. Supponiamo di pensare 4 e di non mentire mai. Il gioco si sviluppa così.

2. Supponiamo di pensare 11 e di mentire alla domanda 4. Il gioco si sviluppa così.

Una curiosità: e se mento a una domanda di controllo?

3. Supponiamo di pensare 7 e di mentire alla domanda 5. Il gioco si sviluppa così.

4. Supponiamo di pensare 13 e di mentire alla domanda 7. Il gioco si sviluppa così.

Risposta

Il sistema è in grado di correggere qualsiasi menzogna. Purché sia una sola!

Materiali per fare esperimenti

Se necessario, fotocopiate più volte questa pagina.

Zio Hamming ti sgamma

Esistono almeno due tipi di codici ridondanti.

• Codici a rivelazione di errore - Consentono di individuare la presenza di un errore.
• Codici a correzione di errore - Consentono non solo di individuare la presenza di un errore, ma anche di identificarne la posizione in modo da poterlo correggere.
  

Un esempio di codice a rivelazione d'errore.

Codice BCD (binary coded decimal) con bit di parità

Per costruire un codice BCDa rivelazione di errore, si può aggiungere ad ogni parola codice(=sequenza di 4 bit)un bit ridondante detto di parità.

Il bit di paritàviene posto a 0 o a 1, in modo tale che la somma degli "1" nella parola codice sia pari.

Esempio di codice a correzione d'errore.

Codice di Hamming Autocorrettivo (4+3)

Per ogni 4 bit d'informazione si hanno 3 bit di controllo di parità.

Si possono disporre i 4 bit d'informazione e i 3 bit di parità nel seguente modo:

Spiegazione:

• il bit 5 (P1) controlla la parità dei bit 1, 2, 3
• il bit 6 (P2) controlla la parità dei bit 2, 3, 4
• il bit 7 (P3) controlla la parità dei bit 1, 2, 4
  

Esempi senza errori.

Esercizio.

Inserite il bit mancante secondo il codice di Hamming presentato in questa pagina.

Una curiosità: i bit di controllo devono stare proprio nelle posizioni 3, 4, 5?

Non necessariamente. Possono stare anche in altre posizioni, ad esempio possono occupare le posizioni:

• 1, 2, 4
• 4, 6, 7

Inoltre possono controllare la parità di gruppi di bit diversi da quelli indicati.

Il disegno in questa medaglia suggerisce che i bit di controllo possono verificare le parità seguenti: bit5 - 1, 2, 3 bit6 - 1, 2, 4 bit7 - 1, 3, 4

Richard Wesley Hamming e il suo gatto.

Esempio con un errore da correggere.

Proviamo a correggere la sequenza errata esaminando tutti i casi possibili.

Soltanto nel caso in cui il bit 2 è errato, la sequenza si può "mettere a posto" cambiando un solo bit. Quindi nella sequenza 1001001, il bit errato è il secondo (da sinistra).

Con il triangolo di Fano, correggere l'errore è più veloce e divertente.

Ricorda: 1 = punto nero, 0 = punto bianco.

Ci sono 4 punti bianchi e 3 neri, ma i 3 neri non sono allineati. Ciò significa che c'è stato un errore. L'unico modo per rientrare in uno dei casi possibili è annerire il punto 2. Il bit errato è il secondo e la sequenza esatta è: 1101001.

Una curiosità: ma il computer, per correggere i bit, disegna il triangolo? O esamina tutti i casi possibili?

No, il computer può soltanto esaminare i bit e confrontarli fra di loro. Perciò deve esistere un algoritmo di correzione degli errori basato soltanto sull'esame dei bit. Vogliamo trovarlo?

Un'altra curiosità: il codice di Hamming è in grado di correggere anche se stesso? Cioè, che cosa accade se è errato un bit di controllo?

Lo verificheremo rispondendo alla domanda precedente.

Ecco un possibile algoritmo.

Dato il seguente codice di Hamming:

Esamino soltanto i tre bit di controllo: P1, P2, P3.

Ricorda che:

• il bit 5 (P1) controlla la parità dei bit 1, 2, 3
• il bit 6 (P2) controlla la parità dei bit 2, 3, 4
• il bit 7 (P3) controlla la parità dei bit 1, 2, 4
  

Dalla tabella si deduce facilmente che:

• Se esattamente 1 di essi è errato allora quello è l'unico errore e i 4 bit d'informazione sono esatti.
• Se sono errati P1 e P2 allora è errato il bit 3
• Se sono errati P1 e P3 allora è errato il bit 1
• Se sono errati P2 e P3 allora è errato il bit 4
• Se sono errati P1, P2 e P3 allora è errato il bit 2
  

E' quindi evidente che il codice di Hamming "corregge anche se stesso" o meglio corregge un qualunque bit errato su 7.

Tre citazioni di zio Hamming

• The purpose of computing is insight, not numbers.
• It is better to do the right problem the wrong way than the wrong problem the right way.
• If you don't work on important problems, it's not likely that you'll do important work.
  

Data creazione: aprile 2006

Ultimo aggiornamento: aprile 2006

xhtml 1.1

Sito Web realizzato da Gianfranco Bo