
[BASE Cinque - Appunti di Matematica ricreativa]
Gianfranco Bo
1. Il commissario Thomas Bayes e la macchina della verità
1b. Il caso del test diagnostico
Una illuminante spiegazione di Enrico Delfini al Forum di BASE Cinque
3b. Caccia al cinghiale
3c. I tre arcieri
4b. Una possibile generalizzazione
4c. Mentire con due sole alternative
Vuoi conoscere la teoria?
Vai alla pagina dell'introduzione alla regola di Bayes, che contiene:
1. Introduzione
2. La regola
3. Se le ipotesi sono più di due?
4. Se qualche dato è variabile?
Nel Paese degli Onesti e dei Sinceri, qualcuno ha rubato la marmellata della nonna.
Baldo è sospettato di aver commesso tale grave delitto.
Poiché non ci sono prove decisive a carico di Baldo, il commissario Thomas Bayes decide di sottoporlo alla Macchina della Verità.
La Macchina della Verità registra alcuni parametri del corpo umano che indicano lo stato d'ansia di una persona: il ritmo della respirazione, la sudorazione delle mani, le pulsazioni cardiache. Sulla base di questi dati, la Macchina stabilisce se l'individuo mente o dice la verità, per mezzo di due luci colorate.
Purtroppo la Macchina della Verità non è perfetta, può sbagliare la valutazione.
Baldo appartiene a una popolazione in cui 5 persone su 1000 sono mentitori, mentre 995 dicono la verità.
Ecco un rapporto dell'interrogatorio di Baldo.
Domanda del commissario: "Baldo, sei stato tu a rubare la marmellata della nonna?"
Risposta di Baldo: "No, io non ho rubato la marmellata della nonna."
Si accende la luce rossa. Ciò significa che Baldo ha mentito.
Il commissario, pensieroso, si domanda: "Qual è la probabilità che Baldo abbia effettivamente mentito dato l'esito positivo della Macchina della Verità?"

Credit immagine: wikiHow (Creative Commons-Attribution-NonCommercial-ShareAlike)
Costruiamo il grafo della situazione.
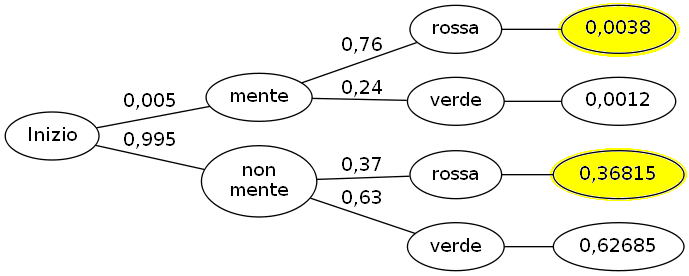
Osserviamo il grafo e rispondiamo alle seguenti domande.
Qual è la probabilità a priori che Baldo sia un mentitore?
La ricaviamo dalle statistica sulla popolazione.
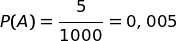
Noi però abbiamo una informazione aggiuntiva:
E = Si è accesa la luce rossa (il test ha dato esito positivo).
Qual è la probabilità totale che si accenda la luce rossa?
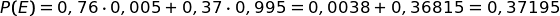
Qual è la probabilità (condizionata) che si accenda la luce rossa nel caso Baldo abbia mentito?
La ricaviamo dalla sensibilità della macchina.
P(E | A) = 0,76
Vogliamo ora calcolare la probabilità a posteriori dell'ipotesi:
P(A | E) = Baldo ha mentito, dato l'esito positivo della Macchina della Verità.
Applichiamo la formula di Bayes:
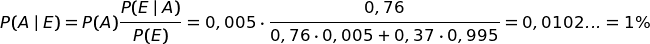
Il grafo ci aiuta a giungere allo stesso risultato con un calcolo più semplice.
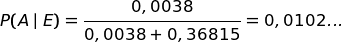
In conclusione, nonostante si sia accesa la luce rossa, l'ipotesi che Baldo abbia mentito è poco probabile (1%) mentre Baldo ha detto la verità al 99%.
Interessante, vero?
A questo punto sarebbe opportuno interrogare la nonna!
Note.
Questo problema è tratto e adattato da Fabio Fagnani, Introduzione alla probabilità in 4 lezioni, Dipartimento di Matematica Politecnico di Torino.
Il funzionamento della Macchina della Verità è molto più complesso di come descritto in questo problema.
Un tipo di problema analogo riguarda l'attendibilità dei test medici diagnostici.
La probabilità che un soggetto abbia una certa malattia è pari a 0,01 (1%).
La diagnosi della malattia è effettuata mediante un test clinico che ha le seguenti caratteristiche:
sensibilità = 0,80 (80% probabilità che un soggetto infetto risulti positivo al test);
specificità = 0,904 (90,4% probabilità che un soggetto sano risulti negativo al test).
1) Qual è la probabilità che un soggetto sia malato dato che è risultato positivo al test?
2) Qual è la probabilità che un soggetto sia malato dato che è risultato negativo al test?
Costruiamo il grafo della situazione.
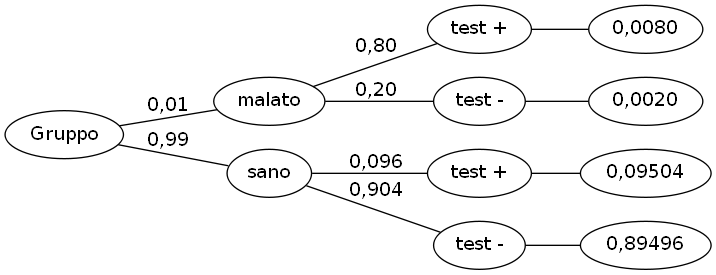
Rispondiamo alla domanda 1)
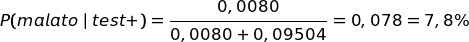
Strano, vero?
Il test dice che uno è malato, ma la probabilità che sia veramente malato - dato il risultato del test - è minore del 10%.
Come si spiega?
Il test dà un falso positivo il 9,6% delle volte e il 99% delle persone sono sane.
Se mettiamo assieme l'alto numero di persone sane e l'abbastanza alta percentuale di falsi positivi, abbiamo come conseguenza una bassa probabilità che chi ha avuto un test positivo sia davvero malato.
Rispondiamo alla domanda 2)
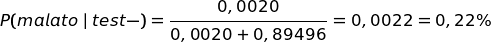
Questo risultato è meno strano di quello precedente. Se il test dice che uno è sano, rimane una probabilità minore dell'1% che l'individuo sia in realtà malato.
Bayes e tutti i problemi e le conseguenze correlate, sono la delizia, ma soprattutto la croce, per chi cerca di insegnare anche solo i rudimenti della statistica applicata alla medicina agli studenti e agli specializzandi.
E anche parlando con colleghi esperti e competenti, che conosco e ammiro da decenni, mi capita spesso (troppo spesso) di incontrare sacche di "ignoranza" che sono dure a morire.
In medicina, il tipo di problema che si deve spesso affrontare, è quello di interpretare il risultato di un test; magari uno screening per identificare tumori e altre patologie.
Ogni test ha due coefficienti: specificità e sensibilità.
Con il primo termine (specificità) si intende la percentuale dei casi che risultano positivi al test e che sono realmente affetti dalla patologia. Più alto è questo numero, minore è la percentuale di "falsi positivi".
La sensibilità, invece, esprime la percentuale dei casi realmente affetti che risultano positivi all'esame. Più alto è questo parametro, minore sarà il numero di "falsi negativi".
Purtroppo, i due parametri sono, in un certo senso, mutualmente escludenti. Se pretendiamo di massimizzarne uno, dobbiamo cedere qualcosa nel secondo. Un certo numero di falsi positivi e di falsi negativi sono ineliminabili.
Oggi, esistono molti test ed esami, che esibiscono valori di sensibilità e specificità apparentemente ottimi e rassicuranti: 90-95-98 %
Ma è giusto sentirsi rassicurati?
L'esempio classico che faccio ai giovani colleghi specializzandi è qualcosa del tipo:
Un certo test per identificare l'infezione da HIV ha una sensibilità del 99,5 % e una specificità del 98%.
Un paziente riceve un test positivo; qual è la probabilità che sia affetto dal morbo? Messa in questi termini, la domanda...non ha risposta. Proprio perché (Bayes insegna), non conosciamo la probabilità a priori; ovvero, in termini clinici, non sappiamo a quale categoria di rischio appartenga il paziente.
Facciamo due esempi, estremi.
A) il paziente è un omosessuale cinquantenne tossicodipendente promiscuo, che vive in Sudafrica
B) una suora di clausura ottantenne che vive da oltre mezzo secolo in un convento abruzzese.
Senza cadere nel pecoreccio e nel cattivo gusto, possiamo prendere per ragionevole una stima di rischio "a priori" del 40% nel primo caso e dello 0,1% nel secondo. Facciamo un paio di conti. Su mille omosessuali, ce ne sono 400 che sono affetti; solo in 2 di questi (lo 0,5%) non verrà scoperto; per contro, dei seicento "sani", il 2%, cioè 12, risulterà erroneamente malato. In totale vedremo 298+12=410 test positivi, per cui la probabilità che il paziente positivo sia davvero malato è 398/410, cioè oltre il 97%.
Passando alle suorine, abbiamo una sola persona realmente malata, che sarà identificata come positiva nel 99,5% dei casi; diciamo per semplicità che viene scoperta. Delle altre 999, ben 20 risulteranno invece falsamente positive. Ricevere un referto positivo, significa ben poco: 20 volte su 21, si tratta di un errore di laboratorio.
Morale? Ogni test ha senso ed è utile se e solo se sappiamo a chi viene rivolto.
E' uno (non il solo) motivo per cui certi test di screening non vengo proposti "a tutti", ma solo a sottogruppi di popolazione. La mammografia, secondo gli epidemiologi più accorti, non dovrebbe essere proposta prima dei 45 anni (secondo alcuni, anche 50); e così la colonscopia per il tumore al colon, eccetera...
Spesso si sente dire che queste scelte sono stupide, sbagliate, che tengono conto solo dei costi... Non è così. Un eccessivo numero di falsi positivi, oltre ad essere un costo, espone un alto numero di persone a stress, esami anche invasivi e potenzialmente rischiosi, con un limitato aumento di casi identificati. Inoltre, e questo raramente viene preso in considerazione, c'è il problema della expertise e della possibile demotivazione del personale impiegato.
Nessuno si augura di fare continuamente diagnosi di cancro, ma oggettivamente il problema esiste. Il radiologo che legge le mammografie, o l'endoscopista che fa la colonscopia, deve poter "contare" su un certo numero di casi positivi ogni mese, per mantenere la competenza e la bravura per identificare le lesioni anche più piccole e difficili. Nessuno può diventare mammografista esperto, vedendo un caso ogni 6-10-12 mesi.
Tornando al caso delle monache, per una popolazione a rischio così basso, sarebbe più conveniente un esame che fosse meno sensibile, ma molto più specifico.
Immaginiamo un test con solo l'80% di sensibilità, ma il 99,9% di specificità.
La suorina malata verrebbe, molto probabilmente, scoperta lo stesso, ma solo un'altra risulterà falsamente positiva. Cosicché, a posteriori, il test positivo sarà corretto nel 50%.
Un simile esame sarebbe molto meno ragionevole proporlo alla popolazione ad altissimo rischio; nel caso A, avremmo al massimo un falso positivo (forse nessuno; e sarebbe un ottimo risultato); ma 80 malati sfuggirebbero all'identificazione.
Baldo è un arciere che centra il bersaglio 1 volta su 6 e dice la verità 4 volte su 5.
Oggi ha lanciato una freccia e ha dichiarato "CENTRO!"
Qual è la probabilità che abbia fatto davvero centro?
Attenzione: in questo contesto, le uniche dichiarazioni che Baldo può fare dopo ogni tiro sono "CENTRO" oppure "NON CENTRO".

Costruiamo il grafo della situazione.
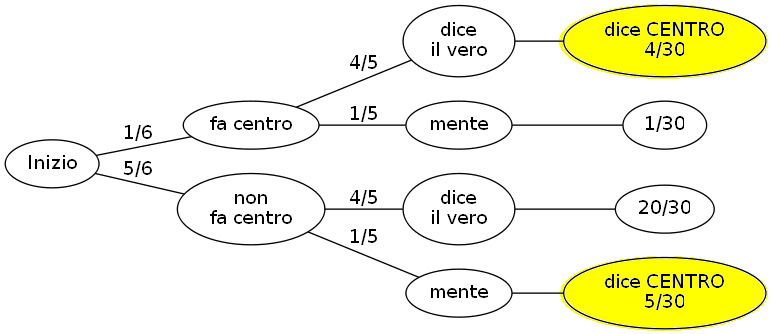
La probabilità a priori che Baldo abbia fatto centro è 1/6.
Vogliamo calcolare la probabilità a posteriori che Baldo abbia fatto centro sapendo che ha dichiarato di aver fatto centro.
Calcoliamo la probabilità dell'ipotesi applicando la formula di Bayes (probabilità composta).
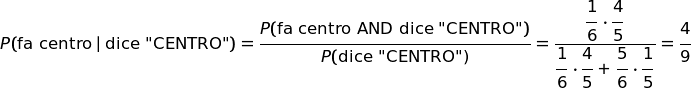
Calcoliamo nuovamente la probabilità con un ragionamento statistico.
Dal grafo risulta che Baldo, in media, dice di aver fatto CENTRO 9 volte su 30 tiri. Ma solo 4 di queste volte ha fatto veramente centro.
Da qui deriva il calcolo:
![]()
Due cacciatori, Aldo e Baldo, durante una partita di caccia, vedono un orso e gli sparano contemporaneamente.
L'orso muore, ma c'é un solo foro di proiettile sul suo corpo.
Nelle condizioni del caso:
I due amici vendono la pelle dell'orso per 70 rubli.
Qual è il modo matematicamente corretto di dividere la somma di denaro fra Aldo e Baldo?

Conveniamo di considerare impossibile che i due proiettili siano entrati in uno stesso foro. Si deduce quindi che uno solo dei due cacciatori ha colpito l'orso. Ma non si sa chi è stato. E non si saprà mai con certezza.
Conveniamo allora di dividere i soldi in parti proporzionali alle probabilità a posteriori che ciascuno dei due amici sia stato la causa della morte dell'orso.
Indichiamo con E, A, B, rispettivamente gli eventi:
E = "Uno solo dei due cacciatori ha colpito l'orso."
Aldo = "Solo Aldo ha colpito l'orso."
Baldo = "Solo Baldo ha colpito l'orso."
Le probabilità a priori sono le seguenti:
La probabilità totale dell'evento E = "Uno solo dei due cacciatori ha colpito l'orso" è:
P(E) = 0,48 + 0,08 = 0,56
Cominciamo col calcolare la probabilità a posteriori della seguente ipotesi:
P(Aldo | E) = probabilità che "Aldo ha centrato l'orso, dato che uno solo dei due cacciatori ha colpito l'orso"
Applichiamo la formula di Bayes.
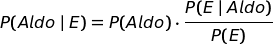
C'è un piccolo problema: quanto vale P(E | Aldo)?
P(E | Aldo) = probabilità che "Uno solo dei due cacciatori ha colpito l'orso" dato che "Solo Aldo ha colpito l'orso"
In questo caso, è evidente che Aldo implica E, perciò:
P(E | Aldo) = 1
Finalmente possiamo calcolare le probabilità a posteriori.
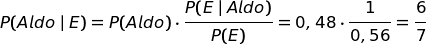
E di conseguenza:
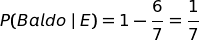
Segue la risposta alla domanda del problema:
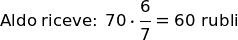
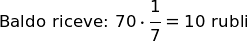
Note.
Questo problema è tratto da: E. S. Wentzel, Probability Theory - First Steps, MIR, Moscow, 1977, 1982 (translated from the Russian by N. Deineko).

Quali sono le origini di questo problema?
Andando a caccia di notizie sull'origine di questo problema ho trovato che un problema simile si trova nel testo:
Aram Arutiunovich Sveshnikov, Problems in Probability Theory, Mathematical Statistics, and Theory of Random Functions, pubblicato per la prima volta (?) in russo nel 1965 e tradotto in inglese nel 1968. (alcune pagine si possono consultare su google books).
A pag 29, il problema 7.9 parla di tre cacciatori che sparano contemporaneamente a un cinghiale. Una sola pallottola colpisce il cinghiale. Le probabilità di fare centro da parte di ciascuno dei cacciatori sonop rispettivamente 0.2, 0.4 e 0.6.
Si chiede di calcolare la probabilità che il proiettile che ha colpito il cinghiale sia rispettivamente del primo, del secondo e del terzo cacciatore.

Un'altra variante del problema della caccia all'orso è il seguente.
Tre frecce vengono lanciate contemporaneamente contro un bersaglio da tre arcieri.
Poiché i tre arcieri sono a distanza diversa dal bersaglio, si stima in:
Se una e una sola freccia colpisce il bersaglio, qual è la probabilità che sia dell'arciere A?
Precisiamo che le frecce sono identiche e non ci sono testimoni che ne hanno seguito le traiettorie. Perciò non è possibile stabilire con prove certe a chi appartiene la freccia che ha colpito il bersaglio.
Risposta: 3/13=23% circa
Il problema dei tre arcieri è stato risolto dettagliatamente:
a) da Giorgio Pietrocola, nel sito Maecla (http://www.maecla.it/matematica/iperproblema/index.htm)
b) da Panurgo, nel FORUM di BASE Cinque (http://www.base5forum.it/tre-arcieri-tre-freccie-una-freccia-t7760.html).
Baldo dice la verità 4 volte su 5.
Baldo estrae a caso un numero della tombola e afferma che è uscito il 35 (I numeri della tombola sono i numeri interi da 1 a 90)
Qual è la probabilità che sia davvero uscito il 35 | sapendo che Baldo ha detto "35"?

Prima di procedere dobbiamo chiarire cosa intendiamo per "dire la verità" e "mentire", in questa situazione.
In particolare, nei casi in cui il numero uscito NON è 35, chi mente dice "35" con probabilità 1/89.
Costruiamo il grafo della situazione.
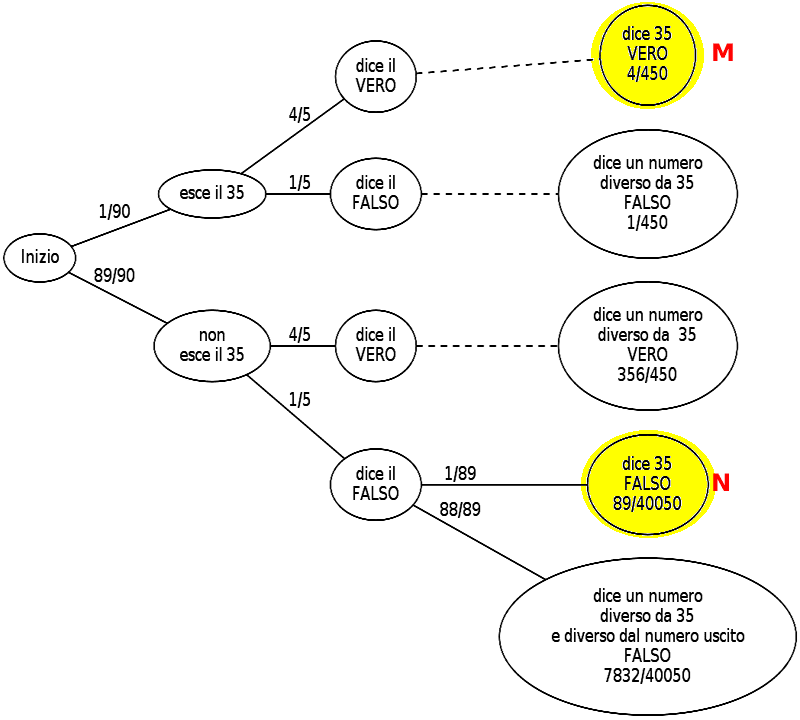
Chiariamo bene la domanda: vogliamo calcolare la probabilità dell'ipotesi:
A = "E' uscito il 35."
condizionata al fatto che:
E = "Baldo ha detto che è uscito il 35."
In simboli:
P(A | E) = Probabilità che "E' uscito il 35" sapendo che "Baldo ha detto che è uscito il 35."
Applichiamo la regola di Bayes (con la probabilità composta).
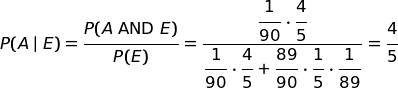
Rifacciamo il calcolo con un ragionamento di tipo statistico-proporzionale.
Osserviamo il grafico, e rispondiamo alle domande.
Con quale probabilità Baldo dice "E' uscito il 35"?
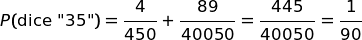
Con quale probabilità è uscito davvero il 35 quando Baldo dice che è uscito il 35?

La probabilità della nostra ipotesi è il rapporto delle due probabilità e risulta 4/5.
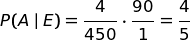
Oppure possiamo ragionare statisticamente così: su 450 prove, Baldo dice "E' uscito il 35" 5 volte, ma solo 4 di queste volte è uscito davvero il 35. La probabilità della nostra ipotesi è data dal rapporto fra i due numeri.
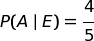
In che modo il grafo può aiutarci per semplificare e generalizzare il calcolo?
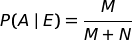
Nel problema precedente, abbiamo visto che i numeri abbastanza alti, che esprimevano probabilità legate alla tombola, si semplificano tutti e alla fine il risultato sembra dipendere soltanto dalla probabilità con cui Baldo dice il vero o mente.
Proviamo allora a generalizzare così:
Riprendiamo il grafo precedente intoducendo le variabili al posto dei numeri.
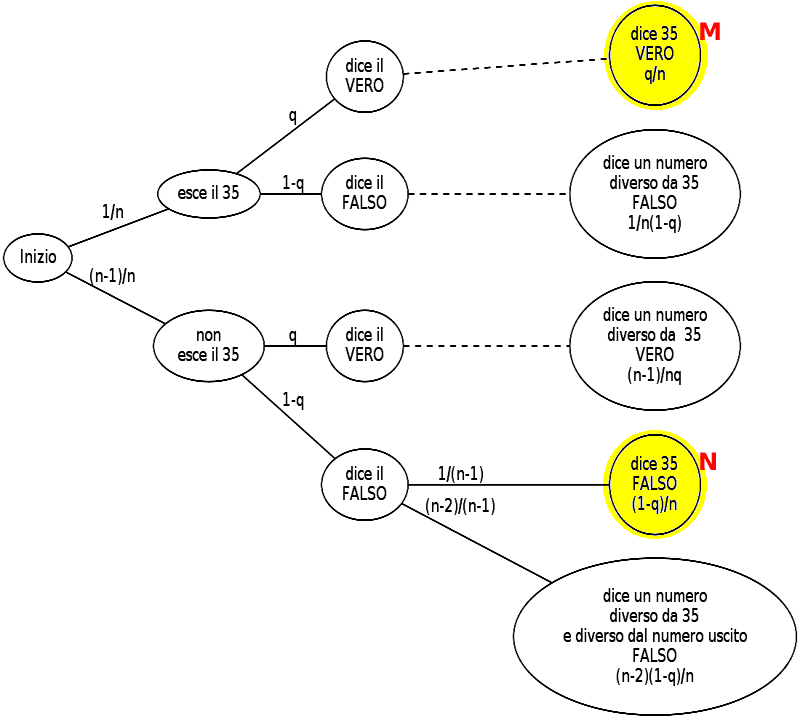
Passiamo senza indugio al calcolo finale, osservando che non dipende da n, anzi è proprio q.
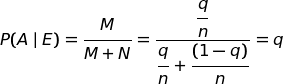
Nota.
La soluzione di questo problema è discutibile.
Infatti, se ammettiamo che quando NON esce il 35 e Baldo mente, possa mentire in un solo modo, dicendo sempre che è uscito il 35, allora la soluzione di questo problema evidentemente cambia.
Un esempio di questa impostazione si trova in: Autori Vari, Xam Idea Mathematics, FK Publications, New Delhi, 2009.
La risposta è 3/8, mentre con il metodo visto sopra dovrebbe essere 3/4.
Il punto dove c'é differenza fra le due soluzioni è quello tra le parentesi arancione.

Se Baldo ha soltanto due possibilità di esprimersi, per esempio A oppure NON-A (vero o falso), allora la soluzione del problema è come quella dell'esempio citato nella nota precedente.
Consideriamo per esempio il seguente problema.
Il grafo della probabilità è il seguente.
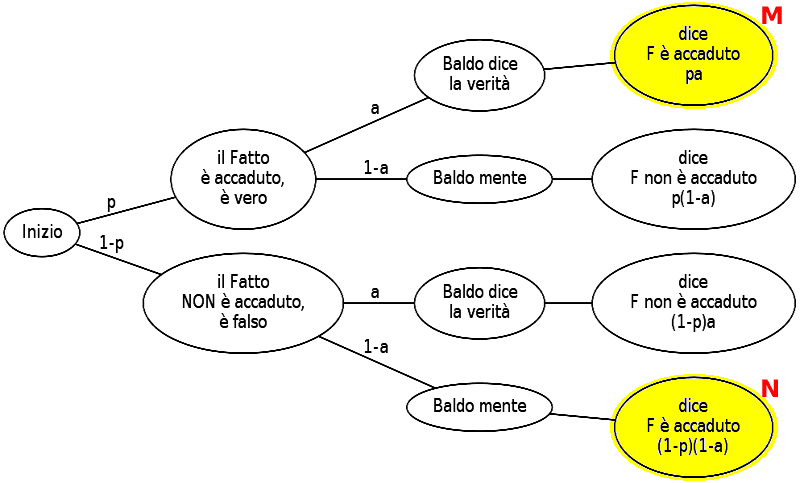
Indicando con:
bisogna calcolare il rapporto:
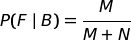
che, con le variabili in gioco, diventa:
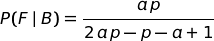
Per esempio, se:
allora:
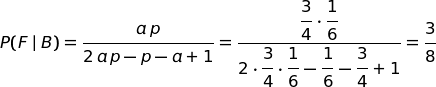
Aldo dice la verità 3 volte su 4 (e quindi mente 1 volta su 4).
Baldo dice la verità 7 volte su 10 (e quindi mente 3 volte su 10).
Un dado viene lanciato sotto gli occhi di Aldo e Baldo.
Entrambi testimoniano che è uscito il 6.
Calcola la probabilità che sia davvero uscito il 6 | sapendo che entrambi i testimoni hanno dichiarato che è uscito il 6.

Prima di tutto dobbiamo chiarire cosa intendiamo per "dire la verità" e "mentire", in questa situazione.
Costruiamo il grafo della situazione. Attenzione, ho scritto solo i dati necessari a risolvere il problema.
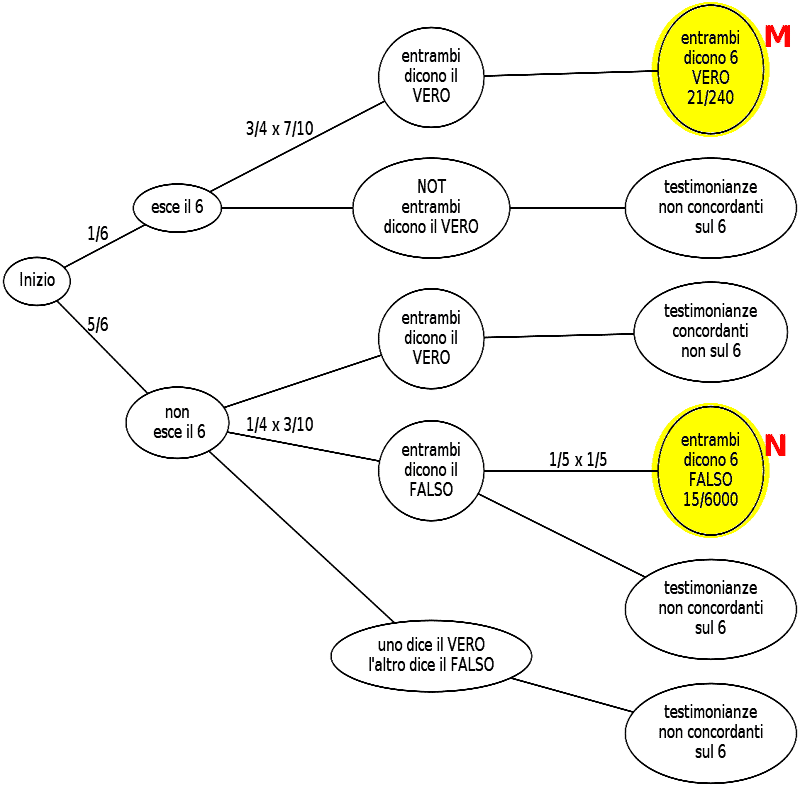
L'ipotesi iniziale è:
A = "E' davvero uscito il 6."
La sua probabilità a priori è ovviamente 1/6.
Ma noi abbiamo un'informazione in più:
E = "Entrambi i testimoni hanno dichiarato che è uscito il 6."
Dobbiamo calcolare la probabilità a posteriori della nostra ipotesi:
P(A | E) = "E' davvero uscito il 6 sapendo che entrambi i testimoni hanno dichiarato che è uscito il 6."
Osserviamo il grafico e applichiamo la regola di Bayes.
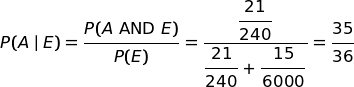
Ripetiamo il calcolo con un ragionamento statistico. Osserviamo il grafico, e rispondiamo alle domande.
Con quale probabilità entrambi dicono che uscito il 6?
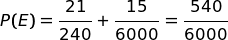
Con quale probabilità è uscito davvero il 6 quando entrambi dicono che è uscito il 6?
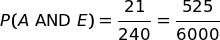
Ora, possiamo ragionare statisticamente così: su 6000 prove, entrambi i testimoni dicono "6" 540 volte, ma solo 525 di queste volte è uscito davvero il 6. La probabilità della nostra ipotesi condizionata è data dal rapporto fra i nue numeri.
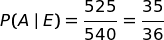
Qual è il modo più breve per calcolare la probabilità richiesta?
Sempre osservando il grafo, abbiamo:
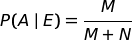
Nota.
Il problema è tratto e adattato da Henry Sinclair Hall, Samuel Ratcliffe Knight, Higher Algebra a Sequel to Elementary Algebra for Schools, Macmillan, 1894.
Parti del libro si possono consultare su Google books.

.
Pace e bene a tutti.
GfBo
Data creazione: 28 luglio 2014
Ultimo aggiornamento: 26 agosto 2014
xhtml 1.1
Sito Web realizzato da Gianfranco Bo