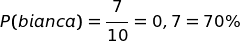
[BASE Cinque - Appunti di Matematica ricreativa]
Ovvero la probabilità delle cause o delle ipotesi.
Gianfranco Bo
Esempio 1 - Problema diretto - facile
Esempio 2 - Problema diretto - difficile
Esempio 3 - Problema inverso (finalmente!)
Dalla soluzione a una formula particolare
Dalla formula particolare a quella generale
Lessico bayesiano
Ripasso
Esempio 4 - Chi ha suonato la campana?
3. Se le ipotesi sono più di due?
Esempio 5 - Il sacchetto misterioso
4. Se qualche dato è variabile?
Esempio 6 - L'ultimo soldato
Vai alla pagina degli esercizi, che contiene:
1. Il commissario Thomas Bayes e la macchina della verità
2. L'arciere bugiardo
3. Caccia all'orso
4. Mentire sulla tombola
5. I due testimoni
Dopo aver studiato la probabilità condizionata, se vogliamo fare un passo avanti significativo, potremmo imparare la formula di Bayes.
In realtà, è molto di più di una formula. E' un modo di pensare che permette di affrontare problemi inversi di probabilità.
Cosa significa?
Cominciamo con tre esempi.
In una scatola ci sono esattamente 7 palline bianche e 3 nere.
Se estrai una pallina a caso, qual è la probabilità che sia bianca?
Soluzione.
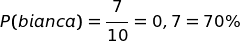
Due scatole, chiamate A, B, contengono 10 palline ciascuna.
Qualcuno sceglie una scatola a caso, lanciando una moneta, e da questa estrae una pallina a caso.
Qual è la probabilità che la pallina sia nera?
Soluzione.
Qui bisogna applicare le formule della probabilità composta e della probabilità totale, che dovresti già sapere.
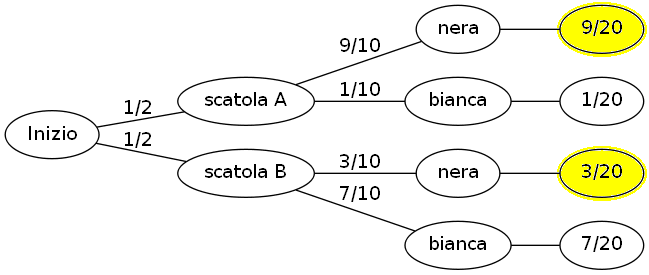
Disegniamo il grafo ad albero delle probabilità in questa situazione. 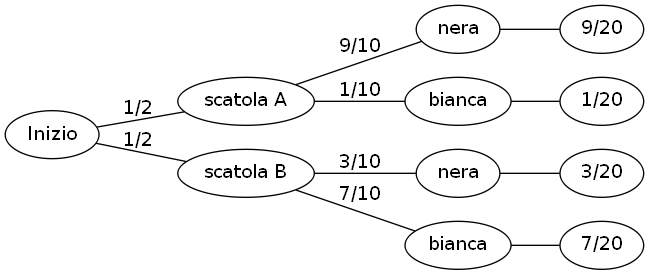
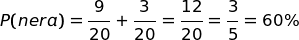
Nota bene.
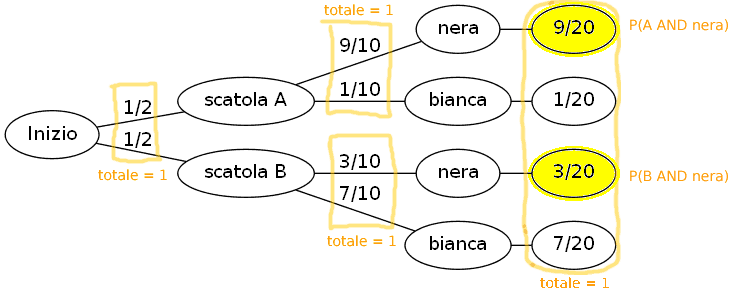
Due scatole, chiamate A, B, contengono 10 palline ciascuna.
Qualcuno sceglie una scatola a caso e da questa estrae una pallina a caso.
La pallina estratta è nera.
Da quale scatola è stata estratta?
Soluzione.
Ammettetelo: sospettate che la pallina nera provenga dalla scatola A, perché ce ne sono 9 su 10, mentre nell'altra ce ne sono molto meno. Questa è un'ipotesi.
Se però voi non sapeste che la pallina estratta è nera dovreste fare due ipotesi a pari merito.
In mancanza di altre informazioni si conviene di assegnare a entrambe le ipotesi la stessa probabilità iniziale che in questo caso è 1/2. Questa si chiama probabilità a priori.
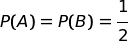
Però abbiamo una informazione in più: la pallina estratta è nera.
Questa nuova informazione ci fa propendere per l'ipotesi A.
Ma di quanto?
Riprendiamo il grafo delle probabilità.

La probabilità totale di estrarre una pallina nera, è:
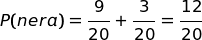
La probabilità (scegliere la scatola A) AND (estrarre una pallina nera) è:

Questi due risultati significano che se facciamo moltissime estrazioni, otterremo statisticamente che:
Quindi possiamo concludere che la probabilità che una pallina nera provenga dalla scatola A è:
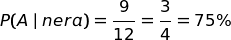
Per scrivere quest'ultimo risultato basta applicare la definizione classica di probabilità di un evento E:
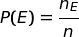
dove nE = numero dei casi favorevoli all'evento E, n = numero dei casi possibili.
Nota bene.
Ripassiamo la soluzione dell'esempio 3 cercando di ricavare una formula matematica.
Usiamo la seguente notazione:
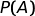 =
probabilità a priori di scegliere la scatola A,
=
probabilità a priori di scegliere la scatola A,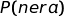 = probabilità
incondizionata di estrarre una pallina nera.
= probabilità
incondizionata di estrarre una pallina nera.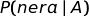 = probabilità di
estrarre una pallina nera condizionata al fatto che si è
scelta la scatola A.
= probabilità di
estrarre una pallina nera condizionata al fatto che si è
scelta la scatola A.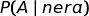 =
probabilità a posteriori che la scatola sia A
condizionata al fatto che la pallina estratta è nera.
=
probabilità a posteriori che la scatola sia A
condizionata al fatto che la pallina estratta è nera.Il nostro procedimento si può sintetizzare con la seguente formula:
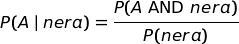
da cui deriva:
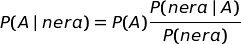
Proviamo ora a generalizzare.
Abbiamo una certa stima della probabilità a priori di un evento A, che possiamo chiamare ipotesi o causa.
Veniamo a sapere che si è verificato l'evento E, che possiamo chiamare effetto.
Allora la probabilità a posteriori dell'evento A, una volta acquisita l'informazione E, é:
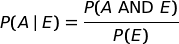
da cui deriva: 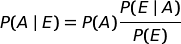 |
Questa è la cosiddetta formula di Bayes.
Da quel che ho capito, ci sono diversi punti di vista filosofici quando si affrontano problemi di probabilità inversa.
Perciò, alcune cose si possono chiamare con nomi diversi.
Dal punto di vi vista matematico, invece, non cambia nulla.
L'evento A si chiama causa e l'evento B effetto.
Quindi, quando calcoliamo 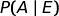 stiamo calcolando la probabilità della causa A in relazione all'effetto E.
stiamo calcolando la probabilità della causa A in relazione all'effetto E.
Questa definizione mette in evidenza l'aspetto oggettivo del calcolo.
L'evento A si chiama ipotesi e l'evento B è una informazione che utilizziamo per valutare l'ipotesi.
Quindi, quando calcoliamo 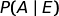 stiamo calcolando l'attendibilità dell'ipotesi A in relazione
all'informazione E.
stiamo calcolando l'attendibilità dell'ipotesi A in relazione
all'informazione E.
Questa definizione mette in evidenza l'aspetto soggettivo del calcolo.
Si chiama così in onore di Thomas Bayes (1702-1761), il matematico e ministro presbiteriano britannico, che (probabilmente?) fu il primo a dimostrarla. La sua dimostrazione fu pubblicata postuma nel 1763.
Stephen Mack Stigler, nell'articolo "Who discovered Bayes's theorem?", The American Statistician, 37, 1983, sostiene che in realtà il teorema di Bayes fu scoperto da Nicholas Saunderson (1682-1739).

Thomas Bayes (?) (1702-1761) |

Nicholas Saunderson (1682-1739) |
Osserviamo amorevolmente la formula:
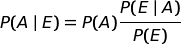
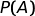 =
probabilità a priori, è la probabilità dell'ipotesi A
prima di sapere che è accaduto E.
=
probabilità a priori, è la probabilità dell'ipotesi A
prima di sapere che è accaduto E.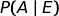 =
probabilità a posteriori, è la probabilità dell'ipotesi
A dopo aver saputo che è accaduto E.
=
probabilità a posteriori, è la probabilità dell'ipotesi
A dopo aver saputo che è accaduto E.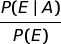 = fattore di
aggiornamento, permette di correggere la probabilità a priori
trasformandola in probabilità a posteriori.
= fattore di
aggiornamento, permette di correggere la probabilità a priori
trasformandola in probabilità a posteriori.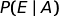 =
verosimiglianza, è la probabilità che accada E
nell'ipotesi A.
=
verosimiglianza, è la probabilità che accada E
nell'ipotesi A.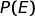 = costante
di normalizzazione, è la probabilità totale che accada E sotto
ogni ipotesi.
= costante
di normalizzazione, è la probabilità totale che accada E sotto
ogni ipotesi.Aldo e Baldo sono due monelli che si divertono a lanciare palline di gomma contro le campane per farle suonare.
Hanno un sacchetto che contiene 4 palline bianche e 6 nere.
Estraggono una pallina a caso: se è bianca, la tira Aldo, se è nera, la tira Baldo.
Si sa che:
Oggi hanno fatto il loro gioco con la campana della chiesa e si è sentito "DONNN".
Chi ha suonato la campana?
Soluzione
Disegniamo il diagramma ad albero delle probabilità.
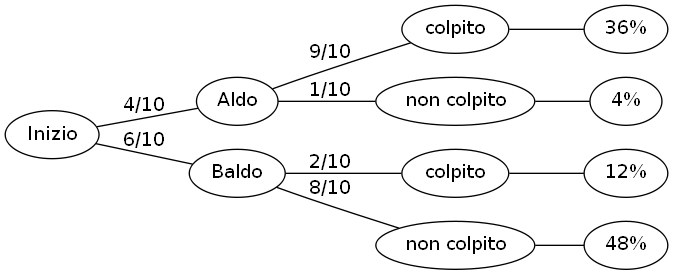
Possiamo fare 2 ipotesi che hanno le seguenti probabilità a priori.
Inoltre sappiamo che:
E = la campana ha suonato.
Valutiamo l'ipotesi A.
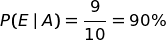 , è la probabilità
che la campana abbia suonato nell'ipotesi che abbia tirato Aldo.
, è la probabilità
che la campana abbia suonato nell'ipotesi che abbia tirato Aldo.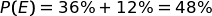 , è la probabilità
totale che la campana abbia suonato sotto ogni ipotesi.
, è la probabilità
totale che la campana abbia suonato sotto ogni ipotesi.Applichiamo la formula di Bayes
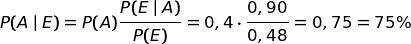
Calcoliamo con lo stesso procedimento l'ipotesi che sia stato Baldo.
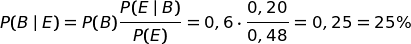
Non dobbiamo applicare la cosiddetta regola di Bayes in modo meccanico. Dobbiamo invece cercare di capire bene la situazione.
Si poteva arrivare agli stessi risultati con altri due metodi.
Medodo 2. Usare la formula delle probabilità composta (normalizzata)
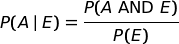
Metodo 3. Usare un ragionamento frequentistico
Dal diagramma delle probabilità si deduce che, in media, ogni 100 lanci la campana suona 36 + 12 = 48 volte.
Di questi 48 "DONNN", 36 sono causati da Aldo e 12 da Baldo.
Quindi, in proporzione:
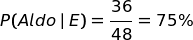
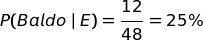
Facile, vero?
| Priori | Posteriori | |
| Ipotesi Aldo | 40% | 75% |
| Ipotesi Baldo | 60% | 25% |
C'é un sacchetto che contiene delle palline, sai che sono 4.
Ci sono alcune palline bianche e alcune nere, ma non sai quante di ogni colore.
Non ci sono palline di altri colori.
Hai diritto a 3 estrazioni, rimettendo ogni volta la pallina estratta nel sacchetto.
Devi scoprire la composizione delle palline nel sacchetto, cioè quante palline nere e quante bianche ci sono.
Come fai?
Soluzione
Facciamo le tre estrazioni ed escono due palline bianche e una nera, {b, b, n}.
Riguardo alla composizione del sacchetto, a priori, abbiamo tre ipotesi equiprobabili che corrispondono alle possibili combinazioni.
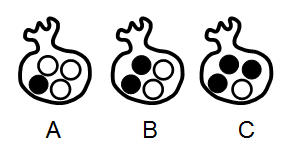
Indichiamo con P(b) la probabilità che esca una pallina bianca e con P(n) la probabilità che esca una pallina nera.
| Ipotesi A | 3 bianche + 1 nera | P(b) = 3/4 | P(n) = 1/4 |
| Ipotesi B | 2 bianche + 2 nere | P(b) = 2/4 | P(n) = 2/4 |
| Ipotesi C | 1 bianca + 3 nere | P(b) = 1/4, | P(n) = 3/4 |
Ma abbiamo un'informazione in più che è il risultato delle tre estrazioni: {b, b, n}.
Calcoliamo la probabilità di questa terna nelle tre ipotesi, applicando la regola della probabilità composta.
Ricordiamo che la terna {b, b, n} (combinazione) può comparire in tre disposizioni diverse: (b, b, n), (b, n, b), (n, b, b), perciò la probabilità di una disposizione va moltiplicata per 3.
| Ipotesi A | 3 b + 1 n | 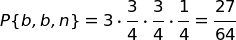 |
| Ipotesi B | 2 b + 2 n | 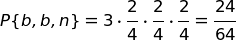 |
| Ipotesi C | 1 b + 3 n | 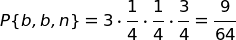 |
Detto questo, disegniamo il grafo della situazione.
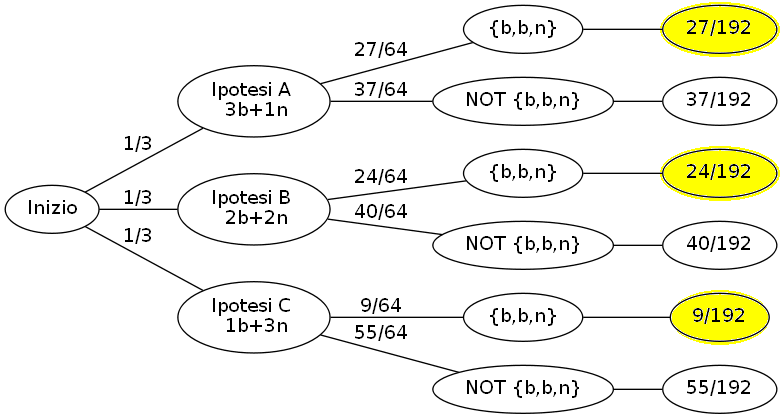
Calcoleremo le probabilità a posteriori delle ipotesi A, B, C con tre metodi diversi.
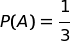 |
è la probabilità a priori dell'ipotesi A |
| E | combinazione estratta {b, b, n}, è l'informazione aggiuntiva |
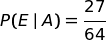 |
è la probabilità di estrarre {b, b, n} nell'ipotesi che il sacchetto contenga 3b + 1n |
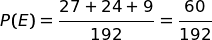 |
è la probabilità totale che esca la combinazione {b, b, n} |
Applichiamo ora la formula di Bayes per valutare l'ipotesi A.
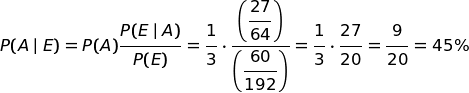
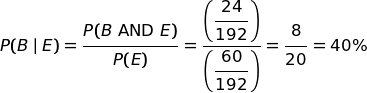
Dal diagramma delle probabilità si deduce che, in media, ogni 192 lanci esce 27 + 24 + 9 = 60 volte la combinazione {b, b, n}.
Nove di queste 60 volte derivano dal'ipotesi C.
Quindi, in proporzione:
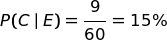
Facile, vero?
| A priori | A posteriori | |
| Ipotesi A | 33,3...% | 45% |
| Ipotesi B | 33,3...% | 40% |
| Ipotesi C | 33,3...% | 15% |
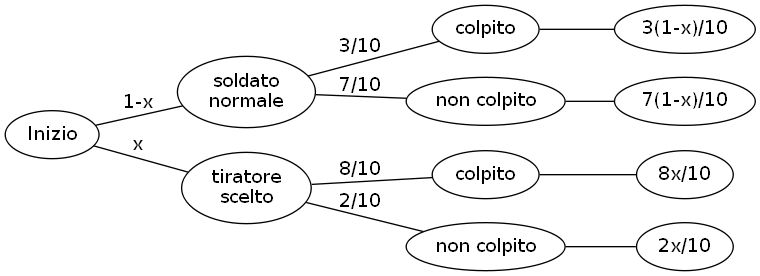
Sei un soldato in combattimento, rannicchiato in una trincea.
Sai per certo che è rimasto UN SOLO soldato nemico sul campo di battaglia, a circa 350 m di distanza.
Sai anche che se il nemico è un soldato normale, ha il 30% di probabilità di colpirti con un tiro da quella distanza.
Ma se invece è un tiratore scelto allora la sua probabilità di colpirti con un tiro da quella distanza è dell'80%.
Ti consoli pensando che i tiratori scelti sono rari, quindi è probabilmente solo un soldato normale. Provi a sbirciare con la testa fuori dalla trincea.
BAM! Un proiettile colpisce il tuo casco militare e ti rannicchi subito nella trincea.
Pensi: "I tiratori scelti sono rari, ma quel tipo mi ha colpito con un proiettile da 350 m di distanza. Forse è un tiratore scelto!"
Dopo pochi minuti, ti fai coraggio e sbirci di nuovo con la testa fuori dalla trincea.
BAM! Un altro proiettile rimbalza sul tuo casco! Giù di nuovo nella trincea.
"Belin," - pensi - "questo dev'essere proprio un tiratore scelto! Farei meglio a chiamare aiuto."
Qual è la probabilità della tua ipotesi che il soldato nemico sia un tiratore scelto?

(Per questo problema, mi sono ispirato a: http://commonsenseatheism.com/?p=13156)
Soluzione.
La probabilità a priori non è indicata nel testo. Tu ti auguri che non sia un tiratore scelto perché i tiratori scelti siano rari ma non hai dati sicuri.
Allora vediamo cosa succede facendo variare la probabilità a priori da 0 a 1. Indichiamola con x.
Disegniamo prima di tutto il grafo ad albero delle probabilità.
Applichiamo la formula di Bayes per esprimere la probabilità a posteriori che il soldato nemico sia un tiratore scelto (P(A | E)).
Usiamo come dato aggiuntivo (E) il fatto che egli ha centrato il tuo casco due volte su due tiri.
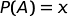 |
è la probabilità a priori che il nemico sia un tiratore scelto. |
| E | ha colpito il tuo casco due volte su due tiri, è l'informazione aggiuntiva |
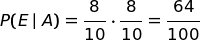 |
è la probabilità che il tiratore scelto ti colpisca 2 volte di seguito |
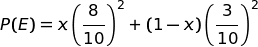 |
è la probabilità totale che tu sia colpito 2 tiri di seguito |
Applichiamo ora la formula di Bayes per valutare l'ipotesi A.
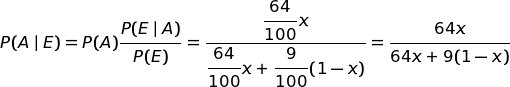
Facendo qualche ulteriore semplificazione, possiamo scrivere una semplice funzione che lega la probabilità a posteriori (y) a quella a priori (x).
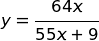
Disegniamo il grafico della funzione, tra 0 e 1. E' evidente che, in questo caso, la formula di Bayes modifica notevolmente la probabilità a priori.
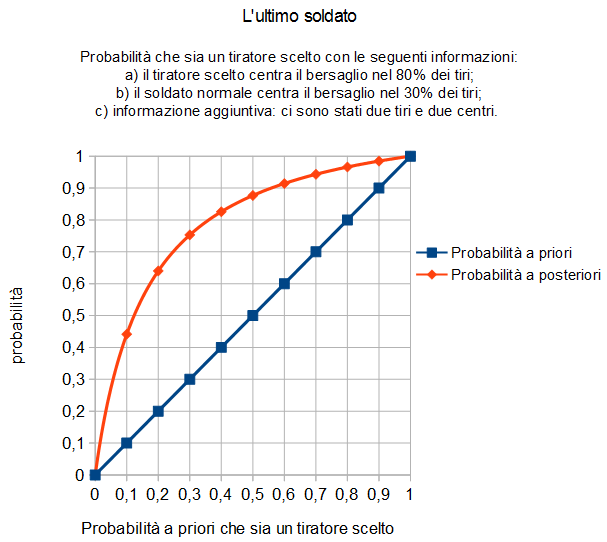
Se vogliamo complicarci la vita, potremmo considerare variabili anche le probabilità di far centro dei due tipi di soldato.
Otterremmo così una funzione a quattro variabili.
Ma questa è un'altra storia...
Comunque, a titolo di esempio osserviamo il grafico seguente in cui il soldato normale è abbastanza abile nel tiro al bersaglio.
In questo caso la differenza fra probabilità a priori e a posteriori si riduce notevolmente.
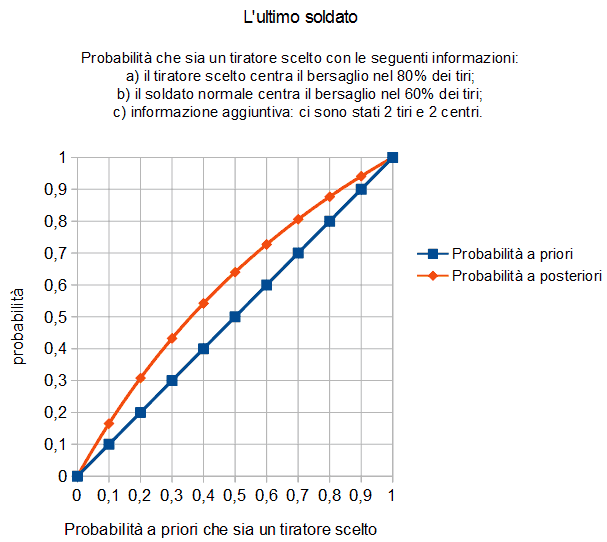
Questo metodo bayesiano è affascinante ma dipende molto dall'affidabilità dei dati iniziali. E questi, a loro volta, sono delle valutazioni di probabilità.
Come facciamo a sapere quanto sono affidabili?
Io non lo so, ma mi viene da pensare che la probabilità delle ipotesi più che essere una misura oggettiva di qualcosa, è una misura soggettiva di quanto noi riteniamo verosimile quel qualcosa stesso.
Non è una critica, è solo una considerazione, magari anche banale, chiedo scusa.
.
Pace e bene a tutti.
GfBo
Data creazione: 28 luglio 2014
Ultimo aggiornamento: 26 agosto 2014
xhtml 1.1
Sito Web realizzato da Gianfranco Bo