
[BASE Cinque - Appunti di Matematica ricreativa]
Vai alle puntate: prima - il quadro, seconda - il problema, terza - il libro
Nella precedente puntata abbiamo esaminato questo dipinto di Bogdanov-Belski che illustra una lezione di matematica del professor Rachinsky.

Nicolai Petrovich Bogdanov Belski (1868-1945)
Aritmetica mentale nella scuola di Rachinski (1895)
Credit: Wikipedia (https://en.wikipedia.org/wiki/Nikolay_Bogdanov-Belsky), il file del dipinto è di pubblico dominio.
Alla scuola di Rachinsky, insieme all'aritmetica e alla grammatica, si studiavano la religione ortodossa, la lingua slava della Chiesa, la pittura delle icone e la musica. Le ragazze imparavano il ricamo e i ragazzi la falegnameria. A scuola c'era un orto, dove i bambini non solo lavoravano, ma studiavano le basi dell'agricoltura, dell'allevamento e dell'apicoltura.
Ma veniamo all'argomento di questa puntata, che è l'esercizio scritto alla lavagna.
Poiché non si distingue bene la scritta, vi riporto il calcolo mentale che il professore aveva posto ai suoi alunni:
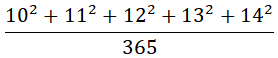
Vi dico che il risultato è 2 e sta a voi scoprire quale proprietà di questi numeri si possa utilizzare per risolvere il calcolo a mente.
E poi, se volessimo generalizzare... sarà questa l'unica successione di 5 termini consecutivi che godono della stessa proprietà?
Ringrazio Simona Riva (Mathmum) per aver inviato questo interessante messaggio al Forum di BASE Cinque!
Questo problema ha suscitato una lunga discussione con tanti messaggi davvero interessanti.
Il link alla discussione è:
https://www.base5forum.it/matematica-arte-e-dintorni-t1035.html?hilit=bogdanov
Qui riporto soltanto due soluzioni: quella di Enrico che spiega come risolvere il problema in modo puramente mentale e quella un più dettagliata di Simona.
Enrico Delfini.
Io faccio i conti così.
Approssimativamente il numeratore è la somma di 5 addendi abbastanza simili.
100 + 121 + 144 + 169 + 196
In prima approsimazione è come moltiplicare l'addendo centrale per 5.
Per fare prima, divido per 2 e moltiplico per 10:
144 x 5 = 144 : 2 x 10 = 720
Adesso devo arrotondare per via del fatto che i 5 addendi non sono uguali:
I due membri delle due coppie di addendi differiscono di +2 e +8, infatti:
25-23 = 2
52-44 = 8
per cui il bilancio dell'arrotondamento è di +10.
720 + 10 = 730, che è il doppio di 365.
Sono tutti conti che si possono davvero fare senza carta e penna
Simona Riva
Se date un'occhiata al quadro, gli studenti (per quanto russi e quindi per definizione ben-educati alla matematica) sembrano "alquanto giovincelli" e quindi probabilmente "poco avvezzi" al calcolo polinomiale (oh, ma come parlo stamattina? sono invecchiata di colpo di 100 anni! )
Come dicevo, l'intento del prof. era insegnare ai suoi studenti come sfruttare le proprietà di certi numeri, in modo da semplificare il calcolo a mente.
Nel nostro caso, i numeri 10, 11, 12, 13 e 14 hanno la caratteristica che
102 + 112 + 122 = 132 + 142
Se scomponiamo adeguatamente il denominatore 365 = 100+121+144 ci accorgiamo in un attimo che il calcolo proposto ha come risultato 2.
La generalizzazione della proprietà utilizzata ci pone il problema: è questa l'unica successione di 5 interi consecutivi, tale che la somma dei quadrati dei primi 3 è uguale alla somma dei quadrati degli ultimi 2?
E qui naturalmente ci basta risolvere un'equazione, come ad esempio:
(x - 1)2 + x2 + (x + 1)2 = (x + 2)2 + (x + 3)2
per avere come soluzione, oltre alla quintupla di cui sopra, anche la quintupla -2, -1, 0, 1, 2.
Queste due quintuple sono anche dette sequenze di Rachinsky.
---
Gli esercizi di matematica che Sergey Rachinsky assegnava ai suoi alunni sono raccolti nel libro 1001 sfide di calcolo mentale, ristampato nel 2017.
La prossima puntata sarà dedicata proprio a questo libro.
Cari amici, sono sicuro che troverete molti spunti interessanti.
Data creazione: luglio 2008
Ultimo aggiornamento: aprile 2020
xhtml 1.1
Sito Web realizzato da Gianfranco Bo