[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Ricreazioni ricevute Gennaio-Giugno 2003
I migliori problemi discussi al Forum di BASE
Cinque
o inviati per posta elettronica
![]()
337. ...
inviato da ...
>>> Risposte & riflessioni
![]()
336. Vedere la torre
inviato da Peppe
Una antica città ha pianta circolare ed è contornata da
una cinta di mura il cui raggio è di 600 metri.
Nelle mura vi sono quattro porte: una a NORD, una a SUD, una ad EST, e la quarta
ad OVEST.
Uscendo dalla porta NORD e dirigendosi in direzione NORD, si incontra una torre
dopo aver percorso 400 metri.
Un uomo esce dalla porta SUD e si dirige verso OVEST: dopo quanti metri potrà
vedere in distanza la TORRE?
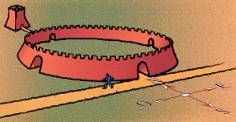
Fonte:Fare Matematica F17
>>> Risposte & riflessioni
Il problema può essere schematizzato come mostrato nel disegno qui sotto.
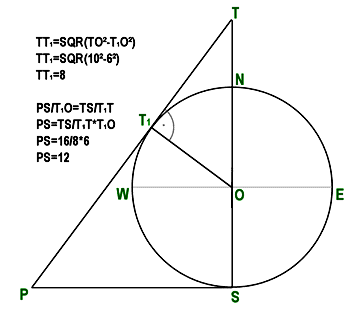
Ringrazio Kay Saupe per aver inviato
questo disegno
e per aver individuato la soluzione esatta che è 1200 m
La città è una circonferenza di centro O e raggio 6 (consideriamo le misure
in centinaia di metri).
Poniamo la circonferenza nel piano cartesiano, con il centro nell’origine.
La sua equazione è allora x2+y2=36.
Le quattro porte sono nei punti di coordinate: N(0;6),W(-6;0),S(0;-6),E(6;0).
Il punto T ha coordinate (0;10).
La retta s ha equazione y = -6; il punto P è intersezione di questa retta e
della tangente alla circonferenza passante per T.
L’uomo che si muove da S lungo la retta s, inizierà a vedere la torre T
quando raggiunge il punto P.
Una retta qualsiasi passante per T ha equazione y = mx+10.
Dal sistema y=mx+10 x^2+y^2=36 ricaviamo l’equazione risolvente:
x^2+(mx+10)^2 = 36
(1+m^2)x^2+20mx+64=0
Ponendo il discriminante uguale a 0, si ha:
400m^2-4*64*1+m2)=0
144m^2-256=0
Quindi m^2=16/9 ed otteniamo: m = (4/3).
Questi due valori di m individuano le due rette,simmetriche rispetto all’asse
y,tangenti alla circonferenza e passanti per T.
Poichè la retta PT ha coefficiente angolare positivo,m=4/3.
La sua equazione è: y = (4/3)x+10
Per trovare le coordinate di P risolviamo il sistema: y = -6 y = (4/3)x+10 da
cui P(-12;-6).
Occorre muoversi dalla porta S, nella direzione Ovest per 1200 metri.
Fonte:Fare Matematica F17
![]()
335. Quadrati e cubi palindromi
inviato da Enrico Delfini
Stiamo per arrivare ad un importante traguardo!!!
Il numero dei visitatori del sito sta rapidamente avvicinandosi a...
No! non a 100 000!
Bensì a 94 249 numero ben noto per essere uno dei rari quadrati palindromi la
cui radice non è un palindromo.
>>> Risposte & riflessioni
cfb
ci credo? non ci credo?
Apro la calcolatrice di windows e digito numeri a caso e ne calcolo il quadrato.
Al terzo tentativo digito
26 il cui quadrato è 676.
Penso:Vuoi vedere che il buon Enrico si è sbagliato?
Altri numeri a caso e di palindromi nemmeno l'ombra......
a questo punto urge il meodo di forza bruta.... apro l'inetrprete basic di
Shiraishi (quello relativo al thread uomo & computer.... uno dei thread cui
sono maggiormente affezionato! eh la passione) e con piacere concludo che anche
questa volta Enrico ha ragione....
Pasquale
Confermo: effettivamente i generatori non palindromi di quadrati palindromi sono
più rari di quelli palindromi,che già di per sé sono rari.
9420645460249 è l'ultimo quadrato palindomo <= 10^14 e viene generato da
3.069.307
Utervis
A noi risulta che il numero:
795.559.265.009.384.106
è il più grande numero non palindromo il cui quadrato sia un palindromo:
632.914.544.142.271.449.944.172.241.445.419.236
composto da ben 36 cifre!
Forse il buon Pasquale è in grado di frantumare anche questo record! :-)))
Pasquale
Beh, ho fatto una piccola ricerca su imternet a riguardo dei palindromi quadrati
(esistono anche i palindromi cubi) ed ho scoperto che esiste una nutrita
comunità che si interessa a questi numeri, dotata di computer da 2 gHz ,
linguaggi veloci e tempo da dedicare (anche qualche mese).
Questi sono alcuni dei risultati (non tutti) a tutt’oggi che superano il
record indicato da Utervis:
2.282.211.769.458.230.805 (19)
5.208.490.560.653.668.833.388.663.560.650.948.025 (37)
25.686.162.978.506.292.366 (20)
659.778.968.558.387.244.939.442.783.855.869.877.956 (39)
637.323.988.797.048.057.098 (21)
406.181.866.696.179.837.389.983.738.971.696.668.181.604 (42)
3.036.233.455.854.775.865.623 (22)
9.218.713.598.451.835.185.192.915.815.381.548.953.178.129 (43)
3.823.177.109.095.314.778.621 (22)
14.616.683.207.510.408.440.555.504.480.401.570.238.661.641 (44)
25.886.574.803.023.261.617.726 (23)
670.114.755.032.518.816.023.606.320.618.815.230.557.411.076 (45)
831.775.153.121.251.039.203.514 (24)
691.849.905.349.880.612.384.525.525.483.216.088.943.509.948.196 (48)
64.897.400.105.515.621.177.314.682 (26)
4.211.672.540.455.378.958.718.869.999.688.178.598.735.540.452.761.124 (52)
Per dare un’idea riporto quanto ha dichiarato un ricercatore:
"The palindromic square number searching algorithm starts by
assuming a generic quadratic formula F(n) = An^2 + Bn + C, where A, B, and C are
non-negative integer numbers. Now the code tries to find palindrome number when
n is within a certain range 'from' to 'to'. It divides the range into subranges
such that for the first and last n within the range F(n) have the same length
and same first digit. For that range, it searches all the last number of n
within 0..9 such that the latest digit of F(n) matches the first digit of F(n).
Now we know when n is within that range, and when n is of the form 10 * m + f,
the first and last digit of F(n) are always the same (f).
After that the code substitute n = 10 * m + f into F(n), remove the highest
digit, divide by 10 to remove the last digit to get F(m). The routine is called
recursively to work on the new formula until the range is small enough to work
with using an iterative algorithm.
I'm using a 1.4Ghz Pentium 4 machine, running Windows XP. Program is written in
Microsoft Visual C++ 6.0. The time the algorithm needs to complete search for
n-digit palindrome squares is around O(10^(n/4)), that is to say time increases
10 times for every 4 digits. Using the current code, I estimate that it will
take around 200 days to complete search all the 52-digit numbers. I hope I can
reduce that to something like 50 days."
Utervis
Ottimo lavoro! Ne eravamo sicuri che riuscivi a fare di meglio.
Vedi se riesci a battere anche il record sui cubi che risulta essere:
2.201³ = 10.662.526.601
Pasquale
Palindromi cubici: pare che sia l'unico.Chissa?
Enrico
Anche a me risulta che che esista solo un cubo palindromo la cui radice non lo
sia.
Qualcuno di voi basecinquini avvezzi all'uso del computer per i lavori di fatica
è in grado di trovare il più grande numero primo palindromo?
a me risulta un "record" di 11811 cifre (palindromo!) che comincia con
1 seguito da 5901 "zero" cui segue un breve nucleo di cifre diverse da
zero, per finire con altri 5901 "zero" e da 1.
cfb
Guardando in giro su internet ho trovato, credo, la stessa comunità citata da
Pasquale.
Il piu' grande palindromo primo "non ancora certificato" è:
47509 volte la cifra 9 un 8 e altri 47509 cifre 9.
si ottiene con la formula 10^95019-1 - 10^47509 ed è pari a 95019 cifre!
Nello stesso sito si parla già di un nuovo record anch'esso da verificare
trovato da Daniel Heuer e avente piu' di 100000 cifre!
PS
piu' passa il tempo e piu' mi rendo conto che la musica e la matematica hanno le
stesse radici e gli stessi meccanismi..... e ne resto affascinato
Utervis
Cfb parla di primi palindromi “non ancora certificati” ...
Enrico accenna di uno “sicuro” con 11.811 cifre ...
Noi aggiungiamo quello “sicuro” scoperto da Harvey Dubner nell’aprile del
1999. E’ un numero di 30.803 cifre che inizia è termina con 1; tra questi due
1 c’è una sequenza di 0, con al centro un altro piccolo palindromo. Senza
scrivere tutti gli zero, il numero è il seguente:
10.000.0..........0.011.101.110.0..........0.001
Il record precedente era sempre di Dubner con il seguente numero di 19.391
cifre, ancora un numero primo palindromo, trovato nel gennaio dello stesso anno:
10.000.0..........0.043.000.340.0..........0.001
![]()
334. Girando per le campagne intorno a casa mia
inviato da Enrico Delfini
Ho visto uno di quei grossi innaffiatori a getto che irrigava un
campo.
Mi sono avvicinato per curiosità, e per godermi una bella doccia in questa
calura, e ho potuto osservare che il getto partiva da un palo posto al centro
esatto di un un podere perfettamente quadrato e che il getto era perfettamente
omogeneo lungo tutti i 360 gradi.
Il contadino mi ha spiegato che il campo misura 40x40 metri e che il getto è
regolabile fino ad una gittata massima di 28,284 metri.
"Il mio problema è che se regolo il getto a 20 metri mi rimane asciutta
una parte del campo ad ogni angolo; se metto la potenza al massimo, innaffio
gratuitamente un bel po' dell'erba del vicino.
Quale gittata consente di minimizzare la somma (terreno mio asciutto + terreno
altrui bagnato)?
A parte la balistica, il succo della mia domanda (pardon, del
contadino!) è questo:
dato un quadrato di lato 40, qual è il raggio del cerchio (con centro al centro
del quadrato) che copre con la maggiore efficienza il quadrato stesso;
considerando come indice di efficienza il cercare di minimizzare la somma delle
aree interne al quadrato non coperte (vicino ai vertici) e di quelle esterne al
quadrato coperte (a metà lato). Con raggio 20 il cerchio è tutto interno, ma
rimane scoperta una area vasta ad ogni angolo; con raggio 28,284 il quadrato è
tutto coperto, ma si copre anche molta superficie esterna...
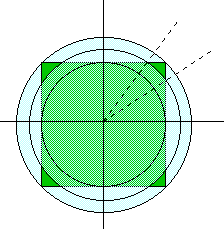
>>> Risposte & riflessioni
Francesco Veneziano
La misura del campo è superflua, quindi possiamo supporre che il lato del
quadrato sia lungo 2; per sentirci più a nostro agio fissiamo un riferimento
cartesiano ortogonale con origine nel centro del quadrato e assi paralleli ai
lati del campo. Per evidenti ragioni di simmetria possiamo limitarci al solo
primo quadrante, e consideriamo la circonferenza x^2+y^2= r^2con1<=r<=sqrt2
A questo punto troviamo l'intersezione tra la circonferenza e il quadrato (sqrt(r^2-1),1)
e scriviamo un po' di integrali, fino ad ottenere un'espressione in r da
minimizzare: (3/2)r^2arctg(sqrt(r^2-1))-(r^2/2)arcsin(1/r)-2sqrt(r^2-1)+1
Derivando e ponendo uguale a 0 devo risolvere
3arctg(sqrt(r^2-1))-arcsin(1/r)=0 cercando la soluzione tra 1 e sqrt2
Naturalmente non sono riuscito a risolvere questo mostro, ma andando un po'
"ad occhio" per tentativi ho stimato che l'angolo tra l'origine e
l'intersezione dovesse essere circa un quarto di tutto il quardante,
controllando questa mia congettura con l'equazione si verifica che è corretta,
infatti ad un angolo di pi/8 corrisponde un raggio di sqrt(4-2sqrt2) che
effettivamente annulla la derivata (si verifica laboriosamente con un po'
ditrigonometria) e spreca 3-2sqrt2 di superficie, che va moltiplicata per 4
perchè ci eravamo ristretti ad un solo quadrante.
In conclusione il raggio del cerchio deve essere sqrt(1-sqrt2/2) = 0.5411961001
(circa) il lato del quadrato, e la superficie spercata è 3-2sqrt2 =
0.1715728752 (circa)la superficie del quadrato.
Ora vorrei sapere da Enrico se conosce qualche dimostrazione di questo fatto che
non sia la mia mostruosità analitica-trigoniometrica e che non richieda mistici
"mi accorgo che..." o "andando ad occhio mi sembra che...";
mi accontenterei anche di una dimostrazione pulita del fatto che l'angolo che
minimizza il tutto è pi/8.
Marco
Si circa e' giusto anche io un po' sperimentando ho trovato quel
valore, anche io son curioso della soluzioni senza seni coseni tangenti e altre
cose del genere.
Francesco Veneziano
In realtà non è strano che un problema facile abbia una
soluzione "difficile", anzi è facilissimo (soprattutto in teoria dei
numeri) produrre problemi semplici e non risolubili con le tecniche attuali. In
geometria poi problemi "naturali" come la quadratura del cerchio hanno
richiesto secoli e un approccio non geometrico per essere risolti.
A dire la verità io non avrei mai sperato di risolvere il tuo problema se non
fossi stato convinto (erroneamente) dell'esistenza di una soluzione elementare;
ho provato un po' a caso solo perchè supponevo che il problema avesse una
soluzione semplice (come in effetti era) anche se di noiosa dimostrazione.
![]()
333. Numero a 5 cifre, ma per 4!
inviato da Desmatron
Esiste un altro interessante quesito simile a questo (il problema 330 sui multipli di 9)...
Qual é quel numero a 5 cifre che moltiplicato per 4 mi dá lo stesso numero al contrario.
... peró sarebbe interessante una dimostrazione matematica piú che un programmino, altrimenti é troppo facile!
>>> Risposte & riflessioni
Pasquale
Indico le 5 cifre con a,b,c,d,e
Perrestarenelle5cifre,deveessere:1<=a<=2, altrimenti se a=3, 4*3=12, il
numero diventa di 6 cifre.
per a= 1,0<=b<=9
per a= 2,0<=b<=4 per la stessa ragione di prima (con 5 c’è un riporto
di 2)
Vediamo cosa accade ad “e”
e>=1, però se moltiplicato per 4, l’ultima cifra del prodotto deve essere
uguale ad uno dei possibili valori di “a” (cioè o 1 o 2)
Solo 3 ed 8 rispettano questa condizione con unico risultato 2 (4*3=12 –
4*8=32)
Dunque:
1) a=2
4*a<>3 anche con eventuali riporti da 4*b, per cui:
2) e=8
Quindi b, che resta compreso fra 0 e 4, quando moltiplicato per 4, non deve dare
riporti, per cui:
0<=b<=2
se b=0, c qualsiasi va bene
se b=1, c qualsiasi va bene
se b= 2,0<=c<=4
Intanto, dal prodotto di 4*e=32, c’è un riporto di 3 da sommare a 4*d ed il
valore dell’ultima cifra deve essere compreso fra quelli di b (cioè fra 0 e
2).
Attribuendo a “d” tutti i valori possibili, moltiplicandoli per 4 ed
aggiungendo 3, si trova che “d” può assumere solo i valori 2 e 7 (4*2+3=11
– 4*7+3=31) e l’ultima cifra è 1.
Quindi:
3) b=1
e 4*b = 4 è diverso dal valore 2 (uno dei possibili di “d”), mentre con un
riporto di 3 dal prodotto 4*c può diventare 7.
Allora:
3) d=7
Situazione:
a..b..c..d..e
2..1.....7..8
4*c più il riporto di 3 da 4*d deve dare a sua volta un riporto di 3 e questo
accade se “c” è uguale a 7, 8 o 9
21778 x 4 = 87112
21878 x 4 = 87512
21978 x 4 = 87912
Pertanto c=9 ed il numero cercato è 21978.
![]()
332. Numeri Felici
inviato da Pasquale
Non ricordo se già sono stati trattati in questo sito, ma ho trovato di recente
dei numeri che vengono definiti FELICI.
Se sommiamo i quadrati delle cifre di un numero e ripetiamo l'operazione sul
risultato e così via, o si entra in un ciclo infinito oppure si termina con 1,
cioè si esce dal ciclo.
I numeri che riescono ad uscire (forse proprio per questo) sono definiti FELICI.
Es: 7 è un numero felice, perché
7^2=49
4^2+9^2=97
9^2+7^2=130
1^2+3^2+0^2=10
1^2+0^2=1
1^2=1
Si chiede di trovare dei numeri felici consecutivi.
Es: 31 e 32 sono 2 numeri felici consecutivi.
Esistono 3 numeri felici consecutivi? e 4 ? etc.
Una precisazione:
Le sequenze indicate non sono le uniche esistenti, ma le prime che si incontrano
(non so se è vero anche per quelle da 6).Ad esempio sono valide anche le
seguenti:
2)129-130
3)4780-1-2
4)8739-40-41-42
5)222688-89-90-91-92
>>> Risposte & riflessioni
Enrico Delfini
La sequenza di tre felici la conosco e mi è molto cara perchè il numero
centrale è l'anno di pubblicazione doi Pinocchio, e un numero
"capovolgibile",
La sequenza di quattro felici non la conosco, ma ne conosco una di cinque!
Utervis
2 numeri consecutivi: ->>>> 31 - 32.
3 numeri consecutivi: ->>>> 1.880 - 1.881 - 1.882.
4 numeri consecutivi: ->>>> 7.839 - 7.840 - 7.841 - 7.842.
5 numeri consecutivi: ->>>> 44.488 - 44.489 - 44.490 - 44.491 -
44.492.
6 numeri consecutivi: ->>>> partire da 111.799...991 (col 9 ripetuto
40 volte) ed arrivare a 111.799...996.
Pasquale
Approfondendo lo studio, secondo me la sequenza di 6 numeri felici consecutivi,
con capofila 1117 seguito da 40 nove e 1, è la prima che si incontra nell’insieme
dei numeri felici.
Riporto inoltre una sequenza di 8 numeri felici consecutivi (comprensiva della
sequenza di 7 consecutivi):
1114 seguito da 4612 sette e da 74, 75, 76, 77, 78, 79, 80, 81 ( numeri da 4618
cifre)
![]()
331. Ovetti in piedi... divertendosi
inviato da Beatrice
Vorrei parlare di galline (ebbene sì, ancora...).
O meglio, di uova.
La mia domanda è semplice.
Un uovo può stare in piedi (senza trucchi)?
E su quanti punti si appoggia? Tre?
Devo preoccuparmi se tutte le mie uova stanno in piedi benissimo e senza alcuno
sforzo?
Perché Colombo ha dovuto rompere un uovo per farlo stare in piedi?
Qualcuno vuole rispondere a questa mia domanda?
Ho sempre sentito dire che l'uovo ha stabilità zero. Tende a sdraiarsi. Il
tuorlo nel centro lo sbilancia e questo cade.
Certi prestigiatori dicono che, sbattendolo violentemente, il tuorlo si posi sul
fondo rendendo più facile la posizione "in piedi". Ma si tratta di un
trucco. Io non lo sbatto; lo appoggio e lui resta in piedi. Talvolta mi bastano
pochi secondi.
Vorrei solo capire se è possibile che un uovo stia in piedi. E come.
Ho consultato tanti siti di matematica, geometria... ma dell'uovo, nemmeno una
traccia.
Voi ci avete provato?
>>> Risposte & riflessioni
Pasquale
Questo lo facevo quand'ero ragazzo e mi riusciva anche posizionandolo
sulla punta piccola: non è facile, ma se il baricentro cade sulla base,
foss'anche un punto solo, l'uovo deve reggersi e si reggerebbe all'infinito se
non vi fossero elementi di disturbo dell'ambiente (vibrazioni, spostamenti
d'aria non percepibili, etc.)
Comunque bisogna fare attenzione, se non si vuole trasformare l'uovo in
frittata.
Gianfranco Bo
Carissimi,
confesso che ho provato a far stare in piedi qualche uovo ma non ci sono
riuscito...
anzi, a dire il vero, alla fine ce l'ho fatta con una goccia di super attack.
A parte gli scherzi, vorrei chiedere a Beatrice di fare un esperimento, per
scoprire se c'è qualche differenza fra uova vere e uova false.
Hai presente quelle uova di legno che si usano per rammendare le calze?
Potresti provare a far stare in piedi una di quelle uova?
E farci sapere i risultati?
Questo potrebbe essere utile per avanzare qualche ipotesi scientifica.
Pasquale, ma davvero ci riuscivi anche tu?
Gianfranco Bo
Incredibile ma vero!
Oggi, 12 maggio 2003, alle ore 22.30 sono riuscito a far star stare in piedi per
la prima volta un uovo!
Ero stremato dai tentativi falliti e mia figlia ormai mi stava compatendo,
mentre guardava la TV (un medico in famiglia).
Alla fine, prima di rimettere le uova nella scatola, ho voluto fare l'ultimo
tentativo.
Il classico ultimo tentativo distratto, senza concentrazione e senza speranza.
Fatto con distacco, come se la cosa non m'interessasse più.
Anzi, tentando l'impossibile: l'uovo in equilibrio sulla punta più stretta.
Ho appoggiato l'uovo sulla tavola, così come capita, e l'ho abbandonato a se
stesso.
Non credevo ai miei occhi, ma quello è rimasto lì, in piedi, immobile.
In preda all'emozione, prima che cadesse, ho esclamato a mia figlia:
"Guarda!"
Lei ha distolto lo sguardo dalla TV e ha guardato, senza dire nulla.
Io, così, per avere una conferma, ho chiesto: "Cos'é?"
E lei: "Un uovo in piedi." come se fosse la cosa più normale di
questo mondo.
Ma la cosa VERAMENTE più strana è che l'uovo non ne voleva sapere di cadere.
Ho dovuto soffiare con una certa energia per buttarlo giù.
Confesso che mi è dispiaciuto.
Bisogna indagare.
Beatrice
Se ci si mette troppa tensione non funziona, io ho notato che sta su dopo un bel
respiro: il classico sbuffo che scioglie la concentrazione e ci aiuta a
recuperare... equilibrio.
Bravo Gianfranco, sono felice del tuo successo.
Ora sei pronto per il cucchiaino...
La prossima volta osserva i movimenti che fa l'uovo poco prima di trovare
l'equilibrio. Non si lascia più cadere mollemente, ma esegue piccoli scatti,
come fosse calamitato. Da lì a poco... resta su.
A me sembra avvolto da un campo magnetico... ma devo dirlo piano su un sito di
matematici.
Non credo possa funzionare con un uovo di legno e quindi è inutile provare...
quando non si è convinti in partenza.
Sto provando a farlo stare sull'orlo di un bicchiere e poi proverò su una
superficie inclinata, l'ho visto fare e dunque sono più convinta. Meglio
sarebbe se ci riuscisse Gianfranco in persona, chi metterebbe in dubbio la sua
esperienza? Attendo con ansia il suo nuovo libro: "Lo Zen e l'arte di
mantenere in equilibrio un uovo". Oppure... perché no... "L'uovo di
Gianfranco Bo".
Mentre a voi lascio il dibattito sulla spiegazione fisica, io continuerò a
cercare in altre direzioni.
E' la più grossa cellula esistente e non sono l'unica a credere che le cellule
posseggano una loro memoria...
Beh, ora me la sono proprio cercata.
(Non lanciatemi uova, però).
Peppe
Stamane il mio entusiasmo per essere riuscito a far stare in piedi (anzi
"dritto" perchè non ha i piedi)un UOVO è stato GELATO da questa
sarcastica risposta di mia moglie:"Che cervello forte!Solo tu puoi fare una
cosa del genere!!"
Potevo dirle che non sono il solo a fare certi esperimenti,ma francamente non me
la sono sentita di coinvolgere gli amici.Ne avrebbe avuto anche per loro...Le ho
risposto solo:
"Perchè non ci provi anche tu?" Mi ha "fulminato" con
un'occhiataccia e girandomi le spalle e ritornata ad occuparsi delle sue
noiosissime faccedende domestiche.
Forse l'UOVO si è risentito più di me perchè non voleva più saperne di
cadere,e io non me la sentivo di rimuoverlo da quella sua "statuaria"
posizione.Ho dovuto soffiare con forza per farlo cadere.
Insomma,confermo anch'io: funziona! Anche se non è facile.
Kaiou
Siccome di uova di gallina non ce n'è neanche l'ombra in casa, ho provato con
le uova di oca, riesce quasi subito, sia dalla base stretta che da quella larga,
ma probabilmente essendo più grandi e pesanti è anche più facile farle
restare in piedi
Merope
Cari amici bentrovati,
una volta si diceva che l'uovo restasse in piedi nel momento
dell'equinozio...infatti in molti paesi del mondo ( ho visto un servizio
televisivo con tanto di ripresa ) il giorno dell'equinozio di primavera si usa
mettere in piedi le uova e lasciarle così finchè non cadono.
Io l'ho provato con i bambini a scuola e ho notato che a certi bambini riesce
più facilmente che ad altri.
Nella mia classe il mettere le uova in piedi è divenuto uno dei riti di
primavera, anzi quest'anno si è diffusa la voce e molte classi ci hanno
seguito.
x Beatrice:
anch'io penso che l'uovo possegga una sorta di memoria e che sia molto sensibile
alle linee di forza che noi ci siamo imposti di non percepire più (sto
esagerando????!!!)
Eugenio
Ci sono riuscito !!!
Basta tenerlo in una mano e far roterare velocemente il braccio in modo tale che
il contenuto dell'uovo per centrifugazione si posizioni nel basso facendo si che
si sposti il baricentro e il gioco e' fatto.
Giovanni Macchia
Purtroppo, io sono uno che le uova le rompe (in ogni senso, ovviamente)
abbastanza spesso e non ho il coraggio di provare per evitare inutili contrasti
con mia moglie.... A parte gli scherzi, prima di venire su questo sito ho letto
l'articolo in inglese che attribuisce questo fenomeno a una nuova teoria di
gravitazione universale scritta dall'autore. Siccome tempo fa , desideroso di
conoscenza, ho avuto la sfortuna per le mie tasche di acquistare un libro di un
docente di fisica che aveva trovato una altrettanto teoria unificatrice che si
era rivelato una vera bufala (tra l'altro voleva sostenere che la scientificita'
di una teoria si dimostra con i disegni), sono andato a leggere la spiegazione.
Chiaramente, si tratta di una teoria senza fondamenti matematici. E inoltre, si
parla di verificabilita' del fenomeno solo in presenza di equinozi . Mah.....
Io penso che almeno una delle seguenti e' una spiegazione scientifica:
1. Secondo me, i rispettivi angeli custodi hanno avuto pieta' di chi ci ha
provato, e hanno esaurito i loro desideri di vedere l'uovo in piedi. Pertanto,
piu' che scentifica, questa sarebbe una dimostrazione dell'esistenza di Dio
2. Le uova si sono stufate di essere maltrattate e, non capendo per quale
diamine di motivo erano disturbate, si sono impermalosite e sono rimaste in
piedi. Questa e' una dimostrazione di vita intelligente sconosciuta.
3. Le uova in realta' sono state scambiate da qualche folletto con uova magiche
che si mantengono da sole in piedi. Questa e' la dimostrazione dell'esistenza di
entita' esterne
4. Il tuorlo d'uovo, se sbattuto, genera un campo gravitazionale che
all'equinozio, per la teoria della relativita' generale di Eintein, gli consente
di rimanere in piedi ( la verificabilita' si dovrebbe avere ascoltando l'uovo
mentre fa delle pernacchiette).
5. L'uovo genera un campo che ferma il tempo e consente a uomini del futuro di
poterlo mantenere in piedi senza essere visti. Questo dimostra che esistono i
viaggi nel tempo.
Scusate, ma quello che ho scritto sopra "alla Zelig" mi e' venuto di
getto (e stavo continuando) quando ho letto tutto quanto avete scritto e spero
che nessuno se ne abbia a male (d'altra parte, meglio divertirsi in qualche
modo..lo dice anche il nome del sogetto...Ovetti in piedi divertendosi..)
Parlando seriamente, il problema principale e' una riproducibilita'
dell'esperimento. Trovare le condizioni per cui un uovo sta in piedi dalla parte
sottile non penso sia facile, ma e' quello che dovrebbe essere fatto. Penso che
l'osservazione di Eugenio sia nella strada giusta; piu' tardi ci provero' a
casa. Se rompo le uova, chiedero' a lui risarcimento...;-))
Beatrice
Novità. Un amico mi ha detto che secondo lui funziona meglio se l'uovo è caldo
(temperatura ambiente). Secondo lui il tuorlo più tiepido scivola verso il
basso e quindi lo rende più stabile. A me non sembra proprio. Il tempo che
impiego non dipende affatto dalla temperatura dell'uovo, né dalla sua forma.
Uso sempre le stesse: a volte stanno su e a volte proprio non vogliono saperne.
Sia che siano fredde di frigo, sia che siano tiepide. Per dirla tutta ho notato
che riesco se sono io la prima a sentirmi equilibrata.
Comunque, secondo le vostre nozioni di fisica, un tuorlo tiepido può dare più
stabilità di un tuorlo freddo? Mi è rimasta la curiosità.
G. Colon
... después de muchos intentos he conseguido poner "de pie" varios
huevos (4), tanto por su parte mas ancha como por su parte más fina...
Es muy curiosa la sensación magnética que se siente en los dedos poco antes de
que el huevo alcance su lugar de equilibrio (el huevo se siente pesado.He notado
que cuando un huevo es sacado recién del refrigerador es más difícil la tarea
(la transpiración de la cáscara lo hace resbaladizo).
He logrado con éxito también poner "de pie" un huevo sobre una
cuchara de sopa, eso si que colocando la cuchara sobre un mantel para que no se
mueva.
He intentado sin éxito poner "de pie" un huevo sobre otro huevo, para
esto basta que el huevo inferior se coloque sobre esos envases en los que se
venden los huevos y luego el otro encima. Creo que no es imposible.
He estado a punto de lograrlo, aunque en todos los casos (dada la finura de la
tarea) se está a punto de lograrlo.
Esto hace las cosas más dramáticas: o se logra o no se logra , no hay
situaciones intermedias.
Requiere cierto equilibrio interno (una persona nerviosa no lo logra).
He pensado que Cristóbal Colón cuando resolvió el asunto del huevo (según la
leyenda: lo posó bruscamente sobre la mesa quebrándolo)fué muy tosco. Aunque
a lo mejor si hubiera sido más fino no habría llegado a nuestras tierras, a
las cuales "pasó a llevar" con igual tosquedad.
desde Chile un saludo a Gianfranco y a Beatrice que me imagino muy delicada.
Pasquale
! Bienvenido Colón !
? Te llamas verdaderamente Colón como Cristóbal ?
Nosotros le llamamos Cristoforo Colombo (Paloma masculina).
Perdone: mi keyboard no puede hacer diferéntemente.
Felicitaciones por tus intentos y resultados con la cuchara de sopa y por tu
equilibrio interno.
Espero pronto de saber que tú hayas puesto con éxito un huevo sobre otro huevo
y después un huevo sobre dos huevos.
Perdone mi Español.
Hasta luego (Pasquale o, si prefieres, Pascual)
G. Colón
...gracias Pasquale por la bienvenida al Forum.
Desde hace un buen tiempo le envío cola(Bo)raciones a Gianfranco y me gusta
mucho el espíritu abierto, alegre, gozoso y lúdico que mentiene este sitio
web.
Entro en al menos una vez al día recorriendo en busca de "buenas
cosas" para oxigenar la docencia.
Ciertamente la docencia que dan los profesores típicos de Matemática es muy
pero muy aburrida. Me gustó mucho la cita de Peano que Gianfranco puso en su
CITARIUM (suena bien esta palabra inventada).
Volviendo a los huevos y su estabilidad precaria: es una muy buena experiencia
para los controlados (que así notan el poder de su control)y también para los
descontrolados (que así notan falta de control).
Desde hace ya varios años que estoy usando el pseudónimo de G. Colón para mis
trabajos de arte.
Un saludo desde este pequeño chile (con minúscula)...a Gianfranco, Beatrice,
Pascuale, ...
Pasquale
! Vale Colón ! ? Si haces pintura, yo también (un poquito) y estó estudiando
Español (un poquito....cuando hablo Español, hablo un poco Italiano y un poco
Español). Mi primera profesora fué Chilena, ahora es una Española (hay
algunas diversidades [de lengua]).....a mi edad no es muy fácil, pero me gusta
mucho.
Chao
![]()
330. Multipli di 9
inviato da Francesco V.
Volevo chiedervi un favore........mi hanno proposto questo
quesito:
Qual'è quel numero di 5 cifre che moltiplicato per nove dà come risultato
lo stesso numero letto al contrario?
>>> Risposte & riflessioni
Gianfranco Bo
Eccoti la risposta al tuo quesito
1089 * 9 = 9801
10989 * 9 = 98901
109989 * 9 = 989901
1099989 * 9 = 9899901
10891089 * 9 = 98019801
10999989 * 9 = 98999901
109999989 * 9 = 989999901
1098910989 * 9 = 9890198901
1099999989 * 9 = 9899999901
....
Come vedi, la serie dei numeri che moltiplicati per 9 dà lo stesso numero
con le cifre disposte in senso inverso è infinita.
Comincia con uno di 4 cifre, poi c'è quello che cerchi tu, e così via...
Ecco un programmino in BASIC che scova tutti i numeri cercati.
Attenzione: l'esecuzione richiede molto tempo; può essere velocizzata
modificando opportunamente il valore di mx.
!'Esistono numeri che moltiplicati per 9
!'diano come il risultato il numero stesso con le cifre
!'disposte in senso inverso?
FOR n = 1 TO 10
LET ini=10^(n-1)
LET fin=10^n-1
LET mx=10^n-1
FOR a = ini TO fin
LET b=a*9
IF b<=mx THEN
LET a$=STR$(a)
LET b$=STR$(b)
LET ok=1
FOR i = 1 TO n
IF
mid$(b$,i,1) <> mid$(a$,n+1-i,1)THEN
LET ok=0
EXIT FOR
END IF
NEXT i
END IF
IF ok=1 THEN PRINT a;"* 9= ";b
NEXT a
NEXT n
END
Giovanni Macchia
Per una versione in notazione matematica, in formato "archivio web", cliccate qui: p330.mht
Ecco invece un modo non basato su "forza
bruta" (cioè programmi) per trovare i numeri di qualsiasi cifra che
soddisfano la richiesta di Francesco.
Per trovare i numeri che godono di questa proprietà con n maggiore o uguale a 5
occorre trovare gli n coefficienti che soddisfano la seguente eguaglianza:
[1] 9a(n)*10^(n-1)+ 9a(n-1)*10^(n-2)+…+ 9a(2)*10+9a(1)= a(1)*10^(n-1)+
a(2)*10^(n-2)+…+ 9a(n-1)*10+a(n)
Affinché rimanga invariato il numero di cifre considerato, dovrà pertanto
essere
a(n)=1 e a(n-1) =0
da cui , poiché 9a(1) = a(n) si ottiene
a(1)=9
valore che sostituito in [1] porta a
9a(2)+8=a(n-1)
da cui si ottiene
a(2) = 8
Per calcolare gli altri coefficienti, notiamo che, sostituendo il valore di a(2)
nella [1] si ottiene
9a(3)+8=10 k(n-2)+a(n-2)
che ammette la soluzione
a(3)=a(n-2)=9, k(n-2)=8
Più in generale possiamo scrivere
[2] 9a(n-m)+k(m+2)=10k(m+1)+a(m+1)
dove3<=(n-m)<=(n-2)
che ammette le soluzioni
[3]a(n-m)=a(m+1)= 9,k(m+1)=k(m+2)=8
Le soluzioni sono pertanto del tipo 109…989 e, per coefficienti a(n-m) tutti
diversi da 0, queste sono le uniche. Per dimostrarlo, consideriamo il caso in
cui (n-m)=n-2 . Sostituendo la [2] nella [1] si ottiene
9a(n-1)+k(m+1)=10k(2)+a(2)
sostituendo i valori di a(n-1) e a(2) si ottiene k(m+1)=8. Sostituendo nella
[2], gli unici coefficienti che soddisfano l'uguaglianza sono quelli trovati
nella [3]. Pertanto i numeri aventi cifre maggiori o uguali a 5 che godono della
proprietà cercata e che hanno coefficienti intermedi diversi da 0 sono tutti e
soli quelli che hanno la forma 109…989. Stante la proprietà di questi numeri,
anche numeri composti da gruppi di uno stesso numero che soddisfa la [1], godono
della stessa proprietà.
Per esempio
109999891099998910999989
gode della proprietà di soddisfare la [1].
Il caso n=4 e' facilmente risolubile alla stessa maniera considerando che ,
essendo di 4 cifre, si ottiene, con ragionamenti simili
a(4)=1, a(3)=0, a(2) = 8 e a(1)=9
![]()
329. Sei città
inviato da Peppe
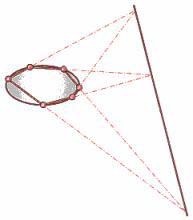
Sei strade, lati di un esagono irregolare, collegano le sei città
A,B,C,D,E,F disposte nel territorio lungo un'ellisse. Si vorrebbe costruire una
tangenziale rettilinea con tre uscite, ciascuna delle quali è allineata con le
coppie di città situate sui lati opposti dell'esagono. Come fare?
Fonte: Fare Matematica F16
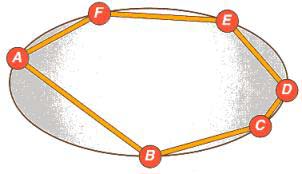
>>> Risposte & riflessioni
I prolungamenti dei lati opposti dell'ESAGONOsi intersecano in
punti tra loro allineati. LaRETTAda essi individuata indica come costruire la
TANGENZIALE.
Fonte: Fare Matematica F16
![]()
328. Piantare gli alberi
inviato da Peppe
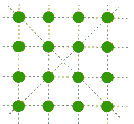
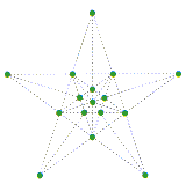
Piantare sedici alberi non disposti su un quadrato come nella
figura accanto,ma in modo tale da ottenere 15 file di 4 alberi ciascuna.
(Fonte: Fare Matematica F9-b)
>>> Risposte & riflessioni
![]()
327. Corde parallele
inviato da Peppe
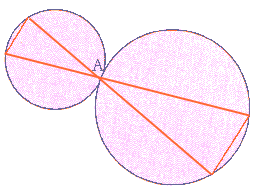
Dati due cerchi tangenti in un punto, comunque si traccino due segmenti per il
punto di contatto , le corde che si formano sono sempre parallele. Perché?
(Fonte: Fare Matematica F9a)
>>> Risposte & riflessioni
I due cerchi sono OMOTETICI ed A è il centro dell’omotetia. Un’omotetia trasforma una retta in una sua parallela.Fonte:Fare Matematica F9a
![]()
326. Guiga, chi era costui?
inviato da Enrico Delfini
Forse è solo la mia ignoranza, ma il nome di Guiga mi era sconosciuto, eppure
ha descritto i NUMERI DI GUIGA che sono quelli che si ottengono così:
si prende un numero (es.: 21)
si individuano i suoi divisori primi (3; 7)
si sommano i reciproci dei fattori primi e si sottrae il reciproco del numero di
partenza (1/3 + 1/7 - 1/21 = 9/21 = 3/7 )
Sono numeri di Guiga quelli in cui tale manipolazione porta a 1
Il più piccolo è 30 (1/2 + 1/3 + 1/5 - 1/30 = 30/30 = 1
Il secondo bisogna cercarlo piuttosto in là (ma prima di 1000)
Buon lavoro
>>> Risposte & riflessioni
Gianfranco Bo
Col solito programmino ho trovato questi
30 = 2*3*5
858 = 2*3*11*13
1722 = 2*3*7*41
66198 = 2*3*11*17*59
Per un errore ho anche inventato i numeri di Guiga-Bo.
Invece di sottrarre il reciproco del numero iniziale, lo si aggiunge, e la somma
deve dare 1.
2 = 2 (1/2+1/2=1)
6 = 2*3 (1/6+1/3+1/2=1)
42 = 2*3*7*43
47058 = 2*3*11*23*31
Sembrerebbe che i numeri di entrambi gli insiemi siano multipli di 6 (tranne il 2)
DIM np(10000)
DIM ft(1000)
PRINT "Creo archivio dei primi 10000 numeri primi"
LET cp=1
LET np(cp)=2
LET ntest=3
DO WHILE cp<10000
LET primo=1
!'LET sq=ntest/2
FOR i=1 TO cp
!'IF np(i)>sq THEN EXIT FOR
IF MOD(ntest,np(i))=0 THEN
LET primo=0
EXIT FOR
END IF
NEXT i
IF primo=1 THEN
LET cp=cp+1
LET np(cp)=ntest
!'PRINT cp;np(cp)
END IF
LET ntest=ntest+2
LOOP
PRINT "Archivio creato"
FOR num=6 TO 100000000
LET n=num
!'PRINT n
LET sommar = -1/n
LET f=1
LET cfatt=0
DO WHILE n>1
IF f<10000 THEN LET df=np(f)ELSE LET df=df+1
DO WHILE MOD(n,df)=0
LET cfatt=cfatt+1
LET ft(cfatt)=df
!'PRINT ft(f); LET n=n/df
!'PRINT n
LET sommar=sommar+1/df
LOOP
LET f=f+1
LOOP
IF sommar=1 THEN PRINT num;
FOR j=1 TO cfatt
PRINT ft(j);
NEXT j
PRINT sommar
END IF
NEXT num
END
Simone G.
Sia N numero naturale,
siano a1,a2,…,an i suoi n divisori
si definisce N numero di Guiga se e solo se:
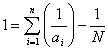
Se ora è giusta questa definizione, da essa discende chiaramente:
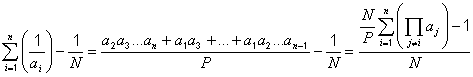
perché P è divisore di N
che unita alla precedente ci dà il passo di iterazione per un eventuale programma decisamente più scarno:
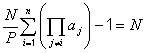
In metalinguaggio:
// trova gli n divisori del numero:
FOR (N=1 to NMAX) //NMAX dipende dal range di valori cui N appartiene (consiglierei il tipo //longint)
//inizializza le variabili
n=0;
s=0;
p=1;
FOR (i=0 to MAX-1) //MAX è una costante a scelta
d[i]=0;
//ricerca i divisori
FOR (i=2 to vN) //crivello di Eratostene
flag = TRUE;
IF (N mod i == 0)
//controlla che i sia numero primo
FOR (j=2 to vi)
IF (i mod j == 0)
flag = FALSE;
IF (flag)
d[n]=i;
n++;
//controlla il passo della definizione
FOR (i=0 to n)
FOR (j=0 to n AND j!=i)
p*=d[j] ;
s+=p ;
p=1;
FOR (i=0 to n)
p*= d[i];
IF (N==((s*N/p)-1)) STAMPA (N)
// FINE DEL CICLO, ricomincia con un nuovo numero
Non so se questo programma funzioni xké sono sotto esami e nn mi sono preso la briga di testarlo, ma non dovrebbe dare grossi problemi.
Peraltro vorrei far notare che se si prendessero come divisori primi anche 1 e il numero stesso, tutti i numei primi sarebbero numeri di Guiga.
![]()
325. Numeri... intoccabili
inviato da Enrico Delfini
Se sommiamo i divisori di un numero, escluso il numero stesso,
ma incluso l'uno, otteniamo alcuni risultati interessanti.
Ovviamente nel caso dei numeri primi, abbiamo 1.
Nel caso dei (rari) numeri perfetti, avremo il numero stesso.
Negli altri casi il risultato sarà un numero, spesso inferiore al numero
generatore, ma talvolta maggiore.
Piccola tabella:
Numero-Somma dei divisori (spero vengano incolonnati).
1________0
2________1
3________1
4________3
5________1
6________6
7________1
8________7
9________4
10_______8
11_______1
12______16
13_______1
14______10
15_______9
16______15
nella colonna di destra appaiono tutti, o quasi, i numeri.
Di quelli mancanti:
l'11 appare alla riga 21;
il 14 compare alla riga 22;
per il 13 dovremo aspettare fino alla riga 27.
Per trovare il 12, bisogna spingersi fino a...??... (PRIMO QUIZ)
Per il 2 e il 5 invece non c'è speranza. Sono essi i numeri INTOCCABILI, secondo una definizione di Erdos.
La sequenza degli intoccabili prosegue:
2-5-52-88-96-120-124-162-188-206-210-.... (ne ho saltato uno: SECONDO QUIZ)
Il 5 sembra essere l'unico dispari, ma non credo sia stato
dimostrato.
Come irrisolta credo sia la questione sulla "infinità" degli
intoccabili.
(da L.Cresci: I numeri celebri- Bollati Boringhieri 2000
>>> Risposte & riflessioni
Pasquale
scusa Enrico, puoi precisare meglio quali sono i divisori di un numero da
sommare ad 1?
Nella tabella che hai riportato come esempio non mi tornano:
4-3
8-7
9-4
12-16
16-15
In 4-3 il 2 l'hai considerato una sola volta, in 8-7 tre volte, in 9-4 il 3 una
sola volta, in 12-16 e 16-15 ?
Enrico Delfini
I divisori di 4 da considerare sono 1 e 2
Per 8 consideriamo 1-2-e 4
Per 12, abbiamo 1-2-3-4 e 6
In pratica prendiamo i numeri per cui il generatore è "divisibile"
senza resto.
C.F.B.
Il 12 sicuramente lo troviamo alla 121 riga (non so se è la sua prima
occorrenza)
121= 1 11
Considerazioni "preliminari" sul perchè i numeri intoccabili sono
pari eccezion fatta per il 5:
Sia D un qualsiasi numero dispari. D puo' essere espresso come D=2x+1.
Ogni numero pari puo' essere espresso come somma di due primi
2x=p1 +p2 (questo andrebbe dimostrato).
allora D lo troveremo alla p1 * p2 riga.
p1 e p2 devono essere diversi da 1 e da x (questo devo approfondirlo).
Esempio.
Sono alla ricerca di 11.
Allora esprimo 10 come somma di 2 primi:
10 = 3+7
11 sicuramente sarà alla 3*7=21 riga.
Il numero intoccabile mancante "dovrebbe" essere 146
![]()
324. Superprimi
inviato da Pasquale
Un Superprimo è un intero tale che tutti i suoi segmenti, letti da sinistra a destra, sono primi (es: in 7193, sono primi 7, 71, 719 e 7193).
Qual è il più grande superprimo ?
>>> Risposte & riflessioni
Enrico Delfini
Sono detti caudati i primi cui si possono togliere le cifre
partendo dalle unità.
Decapitati quelli cui si possono togliere cifre partendo
"da sinistra".
Il più grande caudato, mi risulta essere
73939133
Per i decapitati:
357 686 312 646 216 567 629 137
Ovviamente si escludono i numeri contenenti degli "zeri".
Riguardo al più grande "ambidestro", credo sia
739397
![]()
323. Un intero nella somma
inviato da Pasquale
Un conoscente mi ha posto una domanda che traduco:
esiste un x tale che 1/2 + 1/3 +1/4 +....+ 1/x sia un intero ?
A prima vista mi è sembrato di no, solo per aver visto che nella somma c’è
il periodico 1/3, ma poi ho pensato che suddividendo la somma in somme parziali
la periodicità potrebbe non costituire un vero ostacolo. Es:
1/3 + 1/6 + 1/7 + 1/12 + 1/42 = 3/4
1/9 + 1/12 + 1/15 + 1/36 = 2/5
Tuttavia, non è agevole fornire una risposta con questo sistema ed occorrerebbe
una diversa impostazione di lavoro per dedurre con certezza una risposta
positiva o negativa che sia.
Se la x esiste, certamente è un numero molto grande; la difficoltà del
problema (almeno per quanto mi riguarda) non può costituire ragione valida par
dare una risposta negativa ed anche l’uso del p.c. non è di grande aiuto.
Con il p.c. ho trovato dei quasi interi (es: per x = 740.461.601, la somma vale
circa 20,000.000.000.5 ed ho constatato che con x più grandi si possono trovare
valori con risultati migliori), ma, con un gioco di parole, il circa non è
quello che si cerca.
Cosa ne pensate ? Ciao
>>> Risposte & riflessioni
Francesco Veneziano
Non esiste un tale x, e si può vedere in questo modo:
Sia 2^k la più grande potenza di 2 minore o uguale di x, e sia a l'intero
1/2+1/3+1/4+...+1/x.
allora 1/2+1/3+...+1/(2^k-1)+1/(2^k+1)+...+1/x = a-1/2^k = (a*2^k-1)/2^k
poichè il numeratore è dispari e il denominatore è una potenza di 2 questa
frazione è già ridotta ai minimi termini e il suo denominatore è 2^k.
Sommiamo ora tutte le altre frazioni: il denominatore del risultato è un
divisore del minimo comune multiplo tra tutti i denominatori, e questo NON è
multiplo di 2^k perchè la massima potenza di 2 che compare tra quei
denominatori è 2^(k-1), e quindi quella somma ridotta ai minimi termini non
può avere come denominatore 2^k e siamo arrivati ad una contraddizione.
![]()
322. Dante e la Divina Commedia
inviato da Utervis
Se
"DIVINA COMMEDIA" = 224
quanto vale DANTE?
>>> Risposte & riflessioni
Pasquale
80
![]()
321. L'amore di Gina
inviato da Utervis
"Un giorno entri nella camera vuota di tua sorella Gina; abbandonato sul
letto, trovi stranamente il suo diario personle incustodito. Sei molto curioso
così sfogli velocemente le prime pagine con la speranza di scoprire qualche
notizia piccante. La tua attenzione presto viene attratta da una frase: «Ecco
il mio grande amore!»; di seguito sono riportate queste parole:
EVA - ADAMO = GINA - ?
E' sicuramente una frase in codice che nasconde il nome dell'amichetto di cui è
innamorata Gina. Tu sai per certo che si tratta di uno dei suoi compagni di
classe, ma chi può essere tra DUCCIO, TULLIO, OTTO, GHINO o LEONE?"
Buon divertimento! :-)))
>>> Risposte & riflessioni
Utervis
Allora, visto che è trascorsa una settimana e nessuno ha aggiunto
nulla, forniamo l'aiuto promesso indicando la soluzione "nuda e cruda"
sperando che qualcuno possa capire la logica con la quale vi si giunge.
L'innamorato di GINA può essere solo GHINO!
Ma perchè?
S O L U Z I O N E
Come dicevamo la piccola Gina ha elaborato un efficace sistema per criptare le
sue informazioni personali: le lettere nei nomi maschili hanno il valore del
numero d'ordine che hanno nell'alfabeto italiano a 21 lettere, quindi A = 1, B =
2, C = 3, ..., U = 19, V = 20 e Z = 21; quelle nei nomi femminili hanno invece
il valore del loro numero d'ordine nell'alfabeto italiano, ma cominciando dalla
fine per cui risulta Z = 1, V = 2, U = 3, ..., C = 19, B = 20 ed A = 21. Ogni
lettera che compone il nome, poi, si somma per formare un numero da valutare poi
nell'equazione scritta nel diario. Per cui si ha che:
EVA - ADAMO = (17 + 2 + 21) - (1 + 4 + 1 + 11 + 13) = 40 - 30 = 10
10 = GINA - ? = (15 + 13 + 10 + 21) - ? = 59 - ?
da cui:
? = 59 - 10 = 49
Quindi il nome maschile da sostituire al punto di domanda deve dare come somma
49. GHINO è l'unico che soddisfa questo requisito. Infatti, si hanno:
DUCCIO = 4 + 19 + 3 + 3 + 9 + 13 = 51
TULLIO = 18 + 19 + 10 + 10 + 9 + 13 = 79
OTTO = 13 + 18 + 18 + 13 = 62
GHINO = 7 + 8 + 9 + 12 + 13 = 49
LEONE = 10 + 5 + 13 + 12 + 5 = 45
Dunque l'innamorato di GINA può essere solo GHINO!
Semplice, no? :-)))))))))
![]()
320. I cento lampioni
inviato da Il Cenobita
Posto un problemino postato da porkyporkus su ihe
Supponiamo di avere una strada con 100 lampioni, tutti spenti.
Ogni lampione ha un pulsante, se lo premi quando e' spento il lampione si
accende, se lo premi quando e' acceso lampione si sgegne.
Passa sulla strada un primo uomo che preme il pulsante nei lampioni multipli 1
(tutti).
Poi un secondo uomo che preme il pulsante nei lampioni multipli di 2.
Un terzo uomo i multipli di 3 e cosi' via fino a 100 uomini.
Qual è la situazione dei lampioni (accesi/spenti) dopo il centesimo uomo?
Ma non voglio sapere la soluzione ma una sua implicazione
Si può dimostrare che solo e soltanto i numeri quadrati hanno un numero dispari
di divisori (escludendo 1 e se stessi) ?
>>> Risposte & riflessioni
Francesco Veneziano
Il problema è identico ad un problema dell'ultimo numero del giornalino di
matematica di http://olimpiadi.ing.unipi.it/
e dato che non è ancora uscito il nuovo numero, sarebbe cortese non inserire la
soluzione.
Giorgio Dendi
Accidenti, Francesco: sono stato mezz'ora per scriverla per benino!!!
Va bene, ti ascolto!
Ciao.
![]()
319. Numeri primi gemelli
inviato da Peppe
Due numeri primi sono gemelli, quando la loro differenza è 2.
3 e 5
5 e 7
11 e 13
Recentemente Karl-Heinz Indlekofer e Antal Jàrai hanno scoperto una coppia
'nuova' che batte il precedente record di Forschern di 6320 cifre.
Ogni numero della coppia è formato da 18075 cifre.
I due numeri primi sono:
2 409 110 779 845 x 2^60000 - 1
e
2 409 110 779 845 x 2^60000 +1
Ora io domando ad Enrico & Company,
come si fa a verificarne la veridicità?
>>> Risposte & riflessioni
Enrico Delfini
Esistono infinite coppie di primi gemelli; con una mole di conseguenze...
Sulla verificabilità del dato che riporta Peppe, ho sentito pochi giorni fa una
conferenza di un professore di Informatica a Pisa (pare che sia un genio nel suo
campo) in cui si diceva che, ai fini pratici dell'uso dei computer e dei calcoli
"reali", non gliene importa niente che un dato sia
"vero"; basta che la probabilità di errore sia più piccola di quanto
sia la probabilità che "qualcos'altro vada storto" (tipo: arriva la
fine del mondo; salta la corrente; un'interazione con una particella cosmica
altera il funzionamento di un microchip per un tempuscolo ecc...)
Tra le coppie di primi gemelli; ne esiste una facile facile da ricordare, che
può servire per fare bella figura con gli amici(?)
1 000 000 000 061
1 000 000 000 063
![]()
318. Un'amicizia quadratica
inviato da Peppe
16 dice a 13: „Voglio offrirti un omaggio, in nome della nostra amicizia. Il
mio quadrato è 256 e la somma delle sue cifre è 13".
E 13 risponderebbe: „Grazie per la tua gentilezza, caro amico. Desidero
ripagarti con la stessa moneta.
Il mio quadrato è 169, e la somma delle sue cifre è 16"
In breve:
13 x 13 = 169 ;
1 + 6 + 9 = 16 ;
16 x 16 = 256 ;
2 + 5 + 6 = 13 ;
C'è chi si diverte con poco... Io appartengo a questa categoria...
Citazione:
"Il matematico è un poeta e la Matematica è il suo sogno."
Papy
(E' professore nell'Università di Bruxelles.)
>>> Risposte & riflessioni
![]()
317. Mutazioni-Evoluzioni & Trasformazioni
inviato da Peppe
Nella rubrica curata da Ennio Peres “lettere & cifre” mi ha incuriosito
questa domanda:
Come fa il GATTO a trasformarsi in PESCE ?
Ovviamente questa trasformazione, che sembra una vera e propria “mutazione
genetica”,si effettua applicando le regole del "metagramma", un
gioco ideato da Lewis Carroll, l'autore di "Alice nel Paese delle
Meraviglie",che deve rispettare delle regole precise e si applica a parole
composte dallo stesso numero di lettere.
Ecco le due soluzioni:
1) GATTO-PATTO-PASTO-PESTO-PESCO-PESCE (fornita da un partecipante al forum)
2) GATTO-PATTO-PETTO-PESTO-PESCO-PESCE (quella fornita da Peres)
Dove chiaramente la seconda è più elegante perché il primo passaggio riguarda
il cambio della prima lettera, il secondo quella della seconda, e così via...
E’ possibile fare rinsavire un matto?
Insomma MATTO e SAVIO sono composte dallo stesso numero di lettere,quindi in
teoria è possibile, fare “rinsavire” il matto.
In pratica però mi sembra che ciò sia impossibile in tutti i sensi, (vero
Enrico?) perchè non sono riuscito a compiere il “miracolo” di trasformare
con dei passaggi un MATTO in SAVIO.
Voi ci riuscite?
>>> Risposte & riflessioni
Alan Viezzoli
Così dovrebbe funzionare:
MATTO-PATTO-PALTO'-PALIO-SALIO-SAVIO
Dove SALIO è un "membro di un collegio sacerdotale degli antichi Romani,
dedito al culto di Marte e alle cerimonie relative all'apertura e chiusura
dell'anno militare."
Alessio e Antonio
MATTO
PATTO
PASTO
CASTO
CASTE
CARTE
CARIE
CAVIE
SAVIE
SAVIO
![]()
316. Potenze del due
inviato da sprmnt21
Tutti i numeri di 6 cifre, da 111111 a 999999 sono scritti su
delle carte.
Queste carte sono allineate in un ordine arbitrario.
Dimostrare che il numero risultante, formato da 888889*6 cifre, non è una
potenza di 2.
>>> Risposte & riflessioni
Chiamiamo G il mega-numero.
Possiamo scriverlo in forma polinomiale come somma di tutti i numeri di 6 cifre
moltiplicati per opportune potenze di 10.
Lemma 1
Moltiplicando un numero per una potenza di 10, non cambia il resto
della divisione per 3.
Dim. Se aggiungo degli 0 in fondo al numero, la somma delle cifre è sempre la
stessa.
Lemma 2
Sommando due o più numeri dopo aver tolto gli zeri finali, non cambia
il resto della divisione per 3.
Esempio: (32000 + 7910000) mod 3 = (32 + 791) mod 3 = 1
Dim. Deriva dal Lemma 1
In base ai due lemmi, il problema diventa:
Dimostrare che le somma di tutti i numeri interi da 111111 a 999999 è
divisibile per 3
Per una nota regola delle successioni aritmetiche, tale somma è:
S = (a1+an)*n/2 =
(111111+999999)*888889/2 = 1111110*88889/2
siccome 111110 è divisibile per 3 (e per 2), allora S è divisibile per 3.
Risalendo attraverso i Lemmi posso dire che il mega-numero G è un multiplo di 3
e quindi non può essere una potenza di 2.
![]()
315. Un numero unico al mondo
inviato da Pasquale
Definito “palindromo” un numero che è possibile leggere anche
al contrario (es: 24342), nell'intero universo dei numeri, esiste un solo numero
palindromo “X” con la seguente proprietà:
se dividi “X” per un certo numero “y”, ottieni un altro numero
palindromo e se dividi questo per lo stesso “y” ne ottieni un altro sempre
palindromo e così via, il tutto per 5 volte.
E' possibile ricavare i valori di X ed y anche risolvendo il
seguente anacripto (anagramma criptato):
x^2 - 22x + 85 = 0
(x-2)/3 = 4
(x + 2)/2 = 3
x^3 – 31x^2 + 254x – 224 = 0
x^2 – 19x + 90 = 0
3x +1 = 16
x^2 – 8x + 15 = 0
Ciao a tutti e buon divertimento
>>> Risposte & riflessioni
Gianfranco Bo
Ho passato due pomeriggi molto piacevolissimi a leggermi tutto il forum
di aprile e a mettere nel sito gli interventi che mi hanno colpito di più.
E tra questi c'era anche questo, che è un pesce d'aprile!
Per quel che mi riguarda, non ho fatto il finto tonto, sono stato un vero tonto.
Ho aggiornato la pagina.
Comunque, per non fare una figura proprio di m... ho trovato una soluzione:
15AA51
14641
1331
121
11
1
sono 5 divisioni per 11, in esadecimale...
Potete verificarlo con la calcolatrice di Windows.
C'è un piccolo problema: non so se è l'unico risultato.
Inoltre devo fare i miei complimenti anche a CFB per questo interessante risultato:
1-11-101-131-1111-1441-13231-145541
sono i fattori di 145541
Questo per dire che a questo problema mi ci sto dedicando....

![]()
314. Magia in base 3
inviato da Peppe
Questo è un vecchio gioco con le carte che sfrutta il sistema numerico
in base 3, che molto tempo fa cercai di spiegare, inutilmente , nel Forum di
Base 5.
Il gioco per la prima volta l'ho letto a pagina 135 del libro M. Gardner, Enigmi
e giochi matematici - Vol. V, Sansoni, Firenze, 1976.
Oggi per puro caso l'ho trovato anche sito già segnalato:
http://www2.polito.it/iniziati/polymath/
che a differenza del libro,mostra una foto e uno schema esplicativo relativo
alla distribuzione delle 27 carte utilizzate nel gioco. Ho creato 3 files che ti
allego:
>>> Risposte & riflessioni
Il testo seguente è di Ennio Peres
Come è noto la numerazione in base 3 (o ternaria) è una notazione
posizionale che utilizza solo le tre cifre: 0, 1 e 2. Per convertire in base 10
un numero ternario, bisogna tener presente che (scorrendo le cifre del numero,
da destra verso sinistra) la prima posizione corrisponde alla potenza 3^0, la
seconda alla potenza 3^1, la terza alla potenza 3^2, la quarta alla potenza 3^3,
e così via (procedendo con successive potenze di 3).
Ad esempio, il numero ternario 1102, corrisponde a:
2x3^0 + 0x3^1 + 1x3^2 + 1x3^3 = 2x1 + 0x3 + 1x9 + 1x27 = 2 + 0 + 9 + 27 = 38.
La numerazione ternaria è utilizzata in vari giochi di magia matematica; uno
dei più sorprendenti, noto come "Le pile di Gergonne" (dal nome del
matematico francese che lo studiò per primo), si esegue con le seguenti
modalità.
Presentazione
- Mescolate un mazzo di 27 carte e, dopo averlo consegnato a uno spettatore,
fornitegli le seguenti istruzioni.
1. Scegli mentalmente una di queste carte e ricorda il suo valore, senza
comunicarmelo.
2. Tieni in mano le 27 carte, con le facce rivolte verso il basso e (procedendo
da sinistra verso destra), distribuiscile una alla volta, a faccia in alto, su
righe di 3 carte, fino a formare 3 colonne di 9 carte (come indicato in
figura).(FOTO 1)
3. Dimmi in quale colonna si trova la carta da te scelta.
4. Raccogli in un mazzetto le 9 carte di ciascuna colonna (senza alterare
l'ordine con cui le carte sono state distribuite) e ricomponi il mazzo,
disponendo in un ordine a tuo piacere, i 3 mazzetti così ottenuti.
5. Esegui di nuovo la sequenza di istruzioni 2, 3 e 4 e poi salta al punto 6.
6. Esegui per la terza volta la la sequenza di istruzioni 2, 3 e 4 e poi salta
al punto 7.
7. Distribuisci le carte sul tavolo, nel modo indicato dall'istruzione 2.

- A questo punto siete in grado di indicare, senza alcuna
esitazione, la carta scelta dallo spettatore.
Modalità di esecuzione
Per riuscire in tale intento, dovete osservare i seguenti accorgimenti.
- Ogni volta che lo spettatore ricompone il mazzo (istruzione 4), osservate in
quale posizione: superiore, centrale o inferiore (considerando il mazzo rivolto
a facce in basso), colloca il mazzetto contenente la carta scelta.
- Assegnate a ciascuna posizione una cifra, in base al seguente criterio:
superiore = 0; centrale = 1: inferiore = 2 (in pratica, il valore della cifra
così assegnata corrisponde al numero di mazzetti che vengono messi sopra quello
preso in considerazione).
- Scrivete nell'ordine, da destra verso sinistra, le cifre attribuite alle tre
posizioni osservate, in modo da ottenere un numero ternario; il valore di questo
numero indicherà quante carte, nell'ultima configurazione ottenuta, si trovano
prima della carta da indovinare (contando da sinistra verso destra e dall'alto
verso il basso).
Ad esempio, se la prima volta il mazzetto viene posto nella posizione inferiore
(2), la seconda volta nella posizione superiore (0) e la terza volta nella
posizione centrale (1), scrivendo le relative cifre, da destra verso sinistra,
si ottiene il numero ternario 102. Dato che, in decimale, questo numero
corrisponde a:
2x3^0 + 0x3^1 + 1x2^2 = 2x1 + 0x3 + 1x9 = 2 + 9 = 11,
la carta da indovinare è preceduta da altre 11 carte e, quindi, è la 12^a (in
particolare, se la configurazione finale fosse quella riportata in figura, la
carta da indovinare sarebbe l' Asso di cuori).
Spiegazione del trucco
Per capire il meccanismo su cui si basa questo trucco, bisogna per prima cosa
notare che, se il mazzetto contenente la carta da indovinare venisse posto ogni
volta nella posizione superiore, al termine delle operazioni la carta da
indovinare andrebbe ad occupare la prima posizione in alto a sinistra (ovvero,
non sarebbe preceduta da alcuna carta).
Infatti, se si considera che ad ogni passaggio le carte appartenenti alla
colonna di una data configurazione, dopo essere state raccolte in un mazzetto,
vengono ridistribuite in un gruppetto di 3 righe contigue (composto da 9 carte
in tutto), l'affermazione precedente può essere messa in evidenza dal seguente
prospetto (PROSPETTO)(dove con la lettera A sono indicate le posizioni in cui,
nelle quattro successive configurazioni, può trovarsi la carta da indovinare).
PROSPETTO
|
1a |
2a |
3a |
4a |
|
AAA |
AAA |
AAA |
AXX |
|
AAA |
AAA |
XXX |
XXX |
|
AAA |
AAA |
XXX |
XXX |
|
AAA |
XXX |
XXX |
XXX |
|
AAA |
XXX |
XXX |
XXX |
|
AAA |
XXX |
XXX |
XXX |
|
AAA |
XXX |
XXX |
XXX |
|
AAA |
XXX |
XXX |
XXX |
|
AAA |
XXX |
XXX |
XXX |
Gioco delle 27 carte.
Questo stesso prospetto mostra anche come, dopo ogni operazione di ridistribuzione:
- solo 3 carte appartenenti a un gruppetto di 9, vanno a sistemarsi in una riga occupata da quel gruppetto, al passo precedente;
- solo una carta appartenente a una data riga, va a sistemarsi in una posizione occupata da quella riga, al passo precedente.
Non è difficile verificare che tale assunto è valido anche per gruppetti e per righe, posti in altre posizioni (in questo contesto, però, omettiamo l'analisi dei vari casi possibili, in quanto richiederebbe troppo spazio).
Fatte queste premesse, si può analizzare la situazione generale in cui i mazzetti relativi alle colonne indicate, non vengono posti sistematicamente in cima al mazzo.
In questo caso, alla fine delle operazioni, la carta da indovinare sarà sicuramente preceduta da un certo numero di altre carte, la cui composizione può essere così determinata:
- X gruppetti di 9 carte ciascuno (X = 0, 1, 2), prima di quello contenente la carta da indovinare, se X è il numero dei mazzetti posti sopra quello interessato, nella terza ricomposizione del mazzo;
- Y righe di 3 carte ciascuna (Y = 0, 1, 2), prima della riga contenente la carta da indovinare (all'interno del relativo gruppetto da 9), se Y è il numero dei mazzetti posti sopra quello interessato, nella seconda ricomposizione del mazzo;
- Z carte singole (Z = 0, 1, 2), prima della carta da indovinare (all'interno della relativa riga), se Z è il numero dei mazzetti posti sopra quello interessato, nella prima ricomposizione del mazzo.
In definitiva, il numero totale di queste carte sarà dato da: Zx1 + Yx3 + Xx9, ovvero, coinciderà con il valore del numero ternario: XYZ.
Bibliografia
P. De Frank, Le carte magiche, Hoepli, Milano, 1921 (Copia anastatica,
Cisalpino-Goliardica, Milano, 1975).
M. Gardner, Enigmi e giochi matematici - Vol. V, Sansoni, Firenze, 1976.
M. Gardner, I misteri della magia matematica, Sansoni, Firenze, 1985.
E. Peres, Magia ternaria, dalla rivista Epsilon (Paravia, Torino), n. 12,
novembre 1992.
E. Peres Ventisette carte in fila per tre..., dalla rivista "Res - Cose
d'oggi a scuola" (Elemond, Milano)- n. 15, Febbraio 1998.
C. Rossetti, Magia delle carte, Hoepli, Milano, 1958 (Copia anastatica,
Cisalpino-Goliardica, Milano, 1984).
![]()
313. La spugna
inviato da Giorgio Dendi
Ciao. Scusa se ti scrivo e non mi faccio vedere invece sul Forum.
C'è un problema, quello della spugna, che ho trovato qualche anno fa alle gare
della Bocconi, e poi - mi è stato detto - è apparso su Quark l'anno
scorso, ed è presente anche su internet.
In tutti i casi la soluzione (quella di Quark, quella di internet e
quella presentata su un libro francese che ogni tanto esce con giochi degli anni
precedenti) è più laboriosa - mi pare - di quella trovata da me (ammesso che
sia esatta). Ti interessa? Io non posso mandare in quanto mi sembra abbisognano
di disegni che non riesco a spedire nel forum.
Ecco il testo del problema
Una spugna di forma semicircolare e di diametro 20 cm (come nella
figura, vista dall’alto), viene disposta lungo un lato di un vetro, in modo
che un tocchi l’angolo. Successivamente viene fatta scivolare in modo che alla
fine del movimento l’altro suo vertice tocchi l’angolo. In ogni momento i
due angoli della spugna toccavano i due lati del vetro. Qual è l’area che è
stata pulita? Indicarla in centimetri quadrati, arrotondata al centimetro
quadrato più vicino.

>>> Risposte & riflessioni
Soluzione pubblicata su Enigmes mathematiques pour lyceens et +, volume 18, esercizio 12 e su internet (sito?)
Osserviamo, infatti, che il centro C del diametro AB della spugna si dispone sempre su un quarto di circonferenza di centro O e di raggio dieci centimetri.

In effetti, il triangolo AOB di figura è rettangolo in O, con l’ipotenusa AB di lunghezza costante e pari a 20 centimetri perchè diametro della spugna; inoltre OC è anche la mediana relativa all’ipotenusa di questo triangolo rettangolo. Sia ora L un punto qualunque della spugna; dal teorema per cui in ciascun triangolo ogni lato lato è sempre minore della somma degli altri due, si ricava che OL <= OC + CL. Poichè OC vale dieci centimetri e CL <=10 centimetri, si ricava che qualsiasi punto scegliamo della spugna è sempre OL <= 20 centimetri. Quindi il punto L sarà senz’altro sempre all’interno del quarto di cerchio di centro O e di raggio 20 centimetri colorato in rosso nella figura precedente.
Reciprocamente, dimostriamo che per ogni punto M del quarto di disco di centro O e di raggio 20 centimetri, esiste una posizione della spugna che ricopra tale punto. In effetti, se il punto M è tale che OM è è compreso fra zero e dieci centimetri, allora questo punto è situato o nel semicerchio di centro E e di raggio dieci centimetri (posizione iniziale della spugna) o in quello di centro F e di pari raggio (posizione finale della spugna). Se, invece, il punto OM è compreso fra dieci e 20 centimetri, allora M appartiene al semicerchio di centro C e di raggio dieci centimetri, con C determinato dall’intersezione di OM con l’arco EF. Allora la superficie pulita sarà esattamente pari al quarto di disco di centro O e raggio 20 centimetri. Calcoliamone l’area A:
A = pi·r²/4 = pi·20²/4 = pi·400/4 = pi·100 = 314 centimetri quadrati.
Nota: pi = pi greco = 3,14...
Soluzione di Giorgio Dendi
Suppongo che invece che girare la spugna, sia il vetro a ruotare. Ecco
disegnate la posizione di partenza, due intermedie e quella finale.

Nell’angolo della finestra in ogni istante (tranne l’iniziale
e il finale) vediamo un triangolo rettangolo, formato da due lati del vetro e
dal diametro della spugna che fa da ipotenusa. Un triangolo siffatto è
contenuto in una semicirconferenza. Quindi se mantengo l’ipotenusa (o
diametro) fissa, e sposto il vertice con l’angolo retto, descrivo una
semicirconferenza, che sommata all’altra semicirconferenza, quella fissa della
spugna, forma un cerchio di raggio 10, e quindi di area = 102 pi =
3.14.
© Giorgio Dendi
![]()
312. La torre 2 (variante)
inviato da Pasquale
In una classe di un quinto Liceo Scientifico l'insegnante di
matematica dettò il seguente problema ai propri allievi, tutti bravissimi e da
sempre studenti modello:
"In una torre di base rettangolare il volume è pari a mc. 180 e,
considerati solo dati interi, la somma di uno dei lati della base con
l'altezza è uguale all'incirca all'età di ciascuno di voi, ovviamente espressa
in metri. Calcolare l'area della base della torre."
Dopo circa due ore, nessuno aveva consegnato il compito, quando l'insegnante
disse:
"Dovete scusarmi, ma stamattina ero sovrappensiero, perché stavo pensando
che ieri a casa mia, a tavola, abbiamo corso un brutto rischio..sapete che sono
molto superstizioso, ma per fortuna poi abbiamo trovato una soluzione. Comunque,
bando alle chiacchiere, avevo dimenticato di dirvi che la semisomma dell'altezza
della torre con uno dei lati della base è uguale al numero delle mele che mia
moglie ha comprato ieri al mercato."
Infatti, di lì a poco, tutti consegnarono il compito con la soluzione esatta:
quale?
>>> Risposte & riflessioni
Pasquale
Cerchiamo i dati palesi o nascosti nel testo e procediamo:
Classe 5^ del liceo scientifico e studenti tutti bravissimi da sempre: può
significare che sono al passo con gli studi e la loro età può variare fra i 18
e i 20 anni, ma (se si vuole) anche fra 17 e 21.
Sappiamo che il volume di un parallelepipedo vale S x h, con S =
area di base ed h = altezza della "torre" . A sua
volta: S = a*b, con a = lato corto
e b = lato lungo.
Assumiamo: 0<a<b<h; (per dare al parallelepipedo l'aspetto di una
torre)
Inoltre poniamo: m = a + h; M = b + h; (età dei ragazzi per
ogni combinazione di fattori a,b,h)
Il volume 180 risulta dal prodotto di a*b*h e i loro valori
possibili si deducono da:
180 = 1*2*2*3*3*5.
Elenchiamo quindi tutti gli a,b,h,m,M possibili:
a
b
h
m M
1) 1
2
90
91 92
2) 1
3
60
61 63
3) 1
4
45
46 49
4) 1
5
36
37 41
5) 1
6
30
31 36
6) 1
9
20
21 29
7) 1 10
18
19 28
8) 1 12
15
16 27
9) 2
3
30
32 33
10) 2 5
18
20 23
11) 2 6
15
17 21
12) 2 9
10
12 19
13) 3 4
15
18 19
14) 3 5
12
15 17
15) 3 6
10
13 16
16) 4
5
9
13 14
In base alle affermazioni del testo, consideriamo come valide solo le
combinazioni compatibili con le età dei ragazzi (m ed M) e cioè le
combinazioni 6,7,10,11,12,13 e 14 (se ammettiamo il campo 17-21),
altrimenti restano valide solo le combinazioni 7,10,12 e 13.
Adesso poniamo: n = a + h ed N = b +
h le somme dei lati di base con l'altezza, per ogni
combinazione restata valida, e riportiamo i dati nella seguente tabella:
a
b
h
n N
6) 1 9
20 21 29
7) 1 10
18 19 28
10) 2 5
18 20 23
11) 2 6
15 17 21
12) 2 9
10 12 19
13) 3 4
15 18 19
14) 3 5
12 15 17
Ora, quando il professore aggiunge che la moglie ha acquistato un mumero di mele
uguale alla semisomma dell'altezza della torre con uno dei lati della base,
bisogna considerare che certamente le mele acquistate sono intere, cioè non ci
sono mezze mele, per cui n ed N devono essere pari per essere accettabili.
Quindi restano valide solo le combinazioni 7, 10, 12 e 13 e le mele possibili
nelle combinazioni rimaste sono:
7) 14
10) 10
12) 6
13) 9
Considerando almeno una mela per ogni commensale del giorno precedente, resta da
scoprire quanti erano a tavola.
Poiché siamo in Italia ed il professore è superstizioso, bisogna dedurre che
erano in 13 (a tavola abbiamo corso un brutto rischio) e già per questo,
dobbiamo scegliere 14, ma se consideriamo che in questi casi, i
"molto" superstiziosi (come si autodefinisce il professore)
usano tenersi un invitato di riserva (un vero amico o parente) da aggiungere a
tavola (salvo che all'ultimo momento qualcuno degli invitati non declini
l'invito), in questo caso i commensali erano proprio 14: d'altra parte il
professore afferma che aveva trovato una soluzione.
Quindi, poiché l'unico dato valido resta il 14, abbinato alla combinazione 7,
ne deriva che:
a = 1
b = 10
S = 10
![]()
311. La scacchiera
inviato da Peppe
La scacchiera qui sotto è formata da quadretti il cui lato misura
2 cm.

Qual’è il raggio del cerchio più grande che può essere
disegnato sulla cacchiera in modo che la circonferenza passi interamente
sui quadretti blu?
Fonte:Fare Matematica F8-b
>>> Risposte & riflessioni

La circonferenza più grande ha il centro nel centro di un
quadretto blu e raggio lungo sqrt(10) (ipotenusa del triangolo rettangolo i
cui cateti misurano 1 e 3)
Fonte:Fare Matematica F8-b
![]()
310. Anagramma di una famosa frase euclidea
inviato da Ivana
Insisto con gli anagrammi e, forse, il grande enigmista
basecinquino G.D., suoi impegni permettendo, potrebbe escogitarne altri,
sicuramente migliori...
Si tratta dell'anagramma di una famosa frase euclidea, molto usata soprattutto
in geometria;
sono sicura che riuscirete a individuarla facilmente...
QUESTO RUM ADDORMENTA N.D.
Preciso che si tratta della famosa conclusione delle dimostrazioni di Euclide (cioè della "sentenza", che chiude i ragionamenti , attraverso i quali si ritiene appunto dimostrato l'assunto iniziale).
>>> Risposte & riflessioni
Euclide
Non si può coniare un motto che subito tutti te lo scopiazzano.
1.Ivana è intelligente e spiritosa.
2. Anche le persone intelligenti e spiritose, quando bevono rum, si
addormentano.
3. Ivana se n' è fatta una bottiglia intera
4. Ivana dorme profondamente e sogna anagrammi.
Q. E. D.
Ivana
Bravo Euclide!
QUOD ERAT DEMONSTRANDUM
![]()
309. Il prete e il banchiere
inviato da Pasquale
Un prete incontra un banchiere accompagnato da tre donne.
Il prodotto delle età delle donne è 2450 e la somma è uguale all'età del
prete.
Il prete dice che i dati sono insufficienti per determinare l'età delle donne e
chiede se qualcuna delle tre donne ha la stessa età del banchiere.
La risposta è: "No" e il prete scopre le età delle donne e anche
quella del banchiere.
Quali sono le età?
>>> Risposte & riflessioni
![]()
308. Tecnica matematica e politica
inviato da Ivana
In alcune pagine della tesi di laurea (in matematica) di mia figlia, è stata
citata (e usata) una particolare “tecnica” matematica che io, prima,
conoscevo soltanto come … “strategia” tipicamente politica!
Ho anagrammato la suddetta “tecnica” e penso che voi riuscirete a scoprire,
con facilità, di che cosa si tratta…
Anagramma:
MI DEVI DIRE :”PATE'”
>>> Risposte & riflessioni
Francesco Veneziano
Divide et impera, una delle strategie dimostrative consigliate dai
libri di preparazione alle olimpiadi come l'Engel
Ivana
Dal punto di vista storico-politico, qualcuno ricorda a chi è stata attribuita
tale frase?
Pasquale
Il "divide et impera" è stata ed è una strategia ampiamente
praticata sin dai tempi dell'antica Roma, ma la frase pare che non abbia una
paternità certa.
Qualcuno l'attribuisce a Filippo il Macedone, altri a Luigi XI di Francia.
![]()
307. Problemino: Dante e il Tarlo
inviato da Merope
Su di uno scaffale sono disposti in ordine i tre tomi di un'edizione della
Divina Commedia. Ognuno di essi conta 100 fogli.
Un tarlo particolarmente vorace cominciò a rodere il primo folio del primo tomo
e, procedendo in linea retta, finì col rodere l'ultimo foglio del terzo tomo.
Quanti fogli rose?
da: Bruno D'Amore "Gioco e Matematica" Cappelli
>>> Risposte & riflessioni
Grazia
102 fogli
Peppe
Trattasi decisamente di un tarlo a cui le meravigliose terzine
dantesche non piacciono.
A casa mia una cosa del genere non potrebbe accadere mai:uso la naftalina pure
per i libri(di poesie)!!
Paolo P.
Trattasi pure di tarlo bi-dimensionale, o almeno di spessore inferiore
a quello di una pagina! Se no come farebbe ad arrivare alla pag.1 del tomo 1
senza toccare le altre 99?
Idem per l' uscita.
Gaspero
Possibili risposte:
1ª) primo ed ultimo fogli moolto spessi (cartone), per cui può
"roderli" senza farci un buco "passante"
2ª) da un uovo fatto fra le prime due pagine del primo tomo è nato un tarlo
che poi ha forato la prima pagina ... .per l'uscita sono un po' più in
difficoltà: potremmo supporre che fra le ultime due pagine del terzo volume ci
fosse un segnalibro particolare (una cartolina con l'inchiostro
"cattivo" o una placchetta di rame), per cui arrivato lì è poi
tornato indietro.
Pasquale
Però.....poniamo che il proprietario dei tomi sia disordinato come
qualcuno che conosco: in questo caso, vi sono 6 modi diversi di disporli:
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
e, per ognuno di questi, altri 8 modi diversi, secondo che i tomi siano
capovolti o meno, per un totale di 48 diverse disposizioni.
Escludendo le disposizioni per le quali si ripetono uguali risultati, restano 6
diverse possibilità, in base alle quali il tarlo ideale può smangiucchiare:
2, 101, 102, 200, 201 o 300 fogli.
Enrico Delfini
Non c'entra molto col quesito, ma con il modo di disporre i libri, un
po' sì.
Mi riferisco al fatto che il titolo scritto sul dorso del libro, quello che si
vede quando i libri sono (ordinatamente) disposti sugli scaffali, è scritto a
volte verso l'alto e a volte verso il basso, costringendo, se si vuole dare una
rapida scorsa ai titoli, ad una vera ginnastica cervicale, non sempre gradevole.
Questo per i libri stampati in Italia.
Nei paesi anglosassoni i titoli sono sempre scritti verso il basso.
Non conosco usi e abitudini di altri paesi.
Fortunati i cinesi!!!!
![]()
306. Tre interi
inviato da Gianfranco Bo
Esplorando il newsgroup it.hobby.enigmi ho trovato questo problema
non ancora risolto.
E' stato postato da Dario Uri
3 interi X,Y,Z hanno la seguente proprieta':
X*Y non e' divisibile per Z, difatti c'e' il resto di 1.
X*Z non e' divisibile per Y, difatti c'e' il resto di 1.
Y*Z non e' divisibile per X, difatti c'e' il resto di 1.
Non e' difficile trovare i 3 numeri.
Dimostrare che questa soluzione e' unica.
>>> Risposte & riflessioni
Sprmnt21
Devo controllare per bene alcuni punti, ma credo che quanto segue possa
considerarsi una soluzione valida della questione.
In equazioni il problema si traduce in:
(1)
xy = kz+1
xz = hy+1
yz = lx+1
Da queste si deduce immediatamente che x, y e z sono coprimi. Infatti se, ad esempio x e z avessero un fattore comune questo dovrebbe essere anche fattore di 1 che non puo' essere.
Piu' dettagliatamente, se x=cx' e z=cz' dalla prima delle (1) c(x'y-kz')=1 e questo comporta che c=1. Analogamente per le coppie x,y e y,z.
Supponiamo che due valori della terna siano uguali.
Per fissare le idee poniamo x=y.
La seconda delle (1), in questo caso, diviene x(z-h)=1 che darebbe x=1 come
unico valore che risolve le (1) ma questo non e' accettabile.
La stessa conclusione vale nel caso in cui x=y=z.
Se una terna (x,y,z)=(x*,y*,z*) e' soluzione delle (1),
qualsiasi permutazione di (x*,y*,z*) lo sara'.
Pertanto, senza perdere di generalita', possiamo supporre x < y < z.
Da cui si ricava che k < x ed l > z. Infatti se k>=x, allora
kz>=xz>=xy> xy-1 che contraddice la prima delle (1).
Analogo ragionamento per provare che l>z e che x=<h=<y.
Poniamo h=x+a con 0=<a=<y-x.
Ma se a=0 cioe' h=x avremmo x(z-y)=1 cioe' x=1 e z=y+1 che non sono valori
accettabili.
Dalla II delle (1) si ricava che 1=xz-(x+a)y e sostituendo ad nella I e nella
III delle (1) si ottengono le seguenti relazioni:
(2) y(2x+a)=z(k+x)
e
(3) y(x+z+a)=x(l+z).
Dalla (2) si deduce che z=2x+a. Infatti per quanto provato prima z e y non hanno
fattori comuni percio' z divide 2x+a. Ma nz>x+h=2x+a per n>1.
Dalla (3) si ottiene che z+x+a=mx cioe' 2a=(m-3)x.
Dalla (2) si ha pure che y=k+x<2x cioe' 0<a=<y-x<2x-x=x e quindi
x=2. L'unico valore per a e' pertanto a=1, da cui z=5. Infine essendo
x<y<2x, si ha che y=3.
Percio' (x,y,z)=(2,3,5) e' l'unica terna che risolve le (1).
![]()
305. Congettura anagrammata
inviato da Ivana
Leggendo l'interessante libro "La matematica del Novecento-Dagli insiemi
alla complessità" di Piergiorgio Odifreddi Ed. Einaudi, ho potuto
conoscere una "congettura" moderna, che oso definire "una
bellezza della natura" :-)
L'ho anagrammata:
L'ONU DICHIARA...
Sono sicura che la scoprirete immediatamente
>>> Risposte & riflessioni
Pasquale
CHIARO DI LUNA
Ivana
Esatto.
Bravissimo, Pasquale!
Propongo, ora, un altro anagramma di un concetto matematico
che riguarda, comunque, la congettura Chiaro di Luna
Anagramma
FILMS:"RE","GROSSI ORCHESTIDI"
![]()
304. Eneide
inviato da Ivana
Un grande personaggio di virgiliana memoria si è rivelato un brillante
matematico, risolvendo uno di quei problemi che vengono detti di massimo o
minimo.
Chi è il personaggio e qual è il problema risolto?
>>> Risposte & riflessioni
E' proprio Didone il "brillante" matematico
dell'Eneide...
Ella seppe ricavare dalla pelle di bue una sottilissima corda, con cui
delimitare la massima area possibile, scegliendo un appezzamento di terreno
semicircolare, in riva al mare.
Come precisa Odifreddi nel libro "La matematica del Novecento",
"Didone aveva intuito che il cerchio è la figura che, a parità di
perimetro, ha la massima area: la prima dimostrazione matematica fu data da
Jacob Steiner nel 1838 e completata da Weierstrass nel 1872.
![]()
303. Il corridore
inviato da Zmaster
Un corridore arriva a metà del suo percorso con una media oraria
di 15 Km/h.
A che velocità deve andare nel secondo tratto per arrivare al traguardo con una
media oraria di 30 Km/h?
>>> Risposte & riflessioni
Zmaster
La risposta che molti danno come scontata è 45Km/h.
In realtà la velocità dovrebbe essere infinita.
Ecco il ragionamento che ho seguito: per avere una velocità media doppia (15
-> 30) il corridore dovrebbe percorrere - nello stesso tempo - uno spazio
doppio. Ciò significa che dovrebbe già essere arrivato in fondo, e per fare
ciò dovrebbe percorrere la seconda metà di percorso in un tempo nullo, cioè
ad una velocità infinita.
Non so se mi sono spiegato... :) Questa probabilmente è solo una delle
spiegazioni possibili.
Gianfranco Bo
Chiamiamo:
s, la metà del percorso
2s, l'intero percorso
t1, il tempo impiegato a percorrere la prima metà del percorso
t2, il tempo impiegato a percorrere la seconda metà del percorso
v1, la velocità media con cui è stata percorsa la prima metà del tragitto
v2, la velocità media con cui è stato percorso l'intero tragitto
Si ha che:
v1 = s/t1 = 15 km/h
Se vogliamo che la velocità media sull'intero tragitto sia 30 km/h allora si
dovrebbe avere:
v2 = 2s/(t1 + t2) = 30 km/h
da cui, dividendo per 2:
s/(t1 + t2) = 15 km/h
Ma poiché:
s/t1 = 15 km/h
per realizzare la condizione dovrebbe essere t2 = 0, il che è impossibile per
un normale corridore.
![]()
302. Piramide di sfere
inviato da Manuele Lamarra
Data una piramide di palle di cannone, per cui al primo piano c'e
una palla, al secondo 3, al terzo 6, al quarto 10, al quinto 15...
Chiedo di trovare un'equazione in n, dove n sia il numero di 'piani', il cui
risultato dia la SOMMA TOTALE DEL NUMERO DELLE SFERE DI UNA PIRAMIDE DI n PIANI,
quindi se
n=1
somma=1,
n=2
somma=4
n=3
somma=10
n=4
somma=20
n=5
somma=35
>>> Risposte & riflessioni
Gianfranco Bo
Ringrazio Manuele Lamarra per questo problema che ci da l'occasione per
riflettere sui numeri poligonali e sui numeri poliedrici.
La formula richiesta è la seguente:
|
Tn = |
n(n+1)(n+2) |
|
6 |
ovvero: Tn=(n+2)*(n+1)*n/6
dove n è il numero di "piani" della piramide e Tn è il
totale del numero di sfere che compongono la piramide.
Colgo l'occasione per ricordare un contributo di Marco Pellegrini
sulle relazioni fra i numeri triangolari e tetraedrici (o piramidali) e il
triangolo di Tartaglia.
Generalizzando il discorso dei numeri triangolari di numeri
tetraedrici Tn, definiti da me (e non so se anche da altri) come segue:
Tn e' la somma dei primi n numeri triangolari.
Per cui: T1=1; T2=1+3=4; T3=1+3+6=10; T4=1+3+6+10=20; etc.

20 = 1+3+6+10 è un esempio di numero piramidale
Non e' difficile dimostrare per induzione che:
Tn=(n+2)*(n+1)*n/6.
Tra l'altro questa formula e' il coefficiente binomiale (n+2 su 3),
quindi troviamo tutti i numeri tetraedrici ben allineati nel triangolo di
Tartaglia.
Osservo che anche la formula dei numeri triangolari e' un coefficiente binomiale
(n+1 su 2), e quindi anche i numeri triangolari si trovano tutti ben allineati
nel triangolo di Tartaglia.
![]()
301. La Torre
inviato da Pasquale
In una classe di un quinto Liceo Scientifico l’insegnante di matematica dettò
il seguente problema ai propri allievi, tutti bravissimi e da sempre studenti
modello:
"In una torre a forma di parallelepipedo il volume è pari a 180 metri cubi, il semiperimetro di base è uguale alla lunghezza di quest’aula, mentre la somma di uno dei lati della base con l’altezza è uguale all’incirca all’età di ciascuno di voi, ovviamente espressa in metri. Calcolare l’area della base della torre."
Dopo circa due ore, nessuno aveva ancora consegnato il compito, quando l’insegnante disse ai ragazzi:
"Dovete scusarmi, ma stamattina ero sovrappensiero, perché stavo pensando che ieri sera a casa mia, a tavola, abbiamo corso un brutto rischio ... sapete che sono molto superstizioso, ma per fortuna poi abbiamo rimediato ... Comunque, bando alle chiacchiere, vedendo che, stranamente, nessuno di voi ha risolto il compito ho notato che avevo dimenticato di dirvi che la semisomma dell’altezza della torre con uno dei lati della base è uguale al numero delle mele che mia moglie ha comprato ieri al mercato."
Infatti, con quest'ultimo dato, di lì a poco, tutti consegnarono il compito con la soluzione esatta: quale?
>>> Risposte & riflessioni
Gianfranco Bo
Ringrazio Pasquale per il problema e Utervis
per la dettagliatissima soluzione.
Questo problema è del tipo "Scopri le età di tre persone" sapendo il
loro prodotto, la loro somma e qualche altra informazione che sembra non
entrarci nulla, mentre invece è determinante.
Ho dedicato la pagina L'età delle figlie
ai problemi di questo tipo.
Utervis
L'area di base della torre risulta essere pari a 12 metri
quadrati.Considerando, infatti, intere tutte le misure della torre,
dell'aula in cui sono presenti gli alunni, l'età media di questi ed il numero
delle mele acquistate al mercato il giorno precedente dalla moglie del
professore, partiamo dall'unico dato preciso del problema, che nel caso
specifico è il volume della torre, pari a 180 metri cubi, e scomponiamolo
subito in fattori primi:
180 = 2²·3²·5
Per rispondere al quesito è necessario ora produrre tutte le possibili terne di
numeri interi, rappresentative delle tre dimensioni del parallelepipedo
rettangolo, che, moltiplicati tra loro, producono 180 metri cubi di volume.
Dobbiamo considerare, però, che uno dei tre spigoli, od al massimo anche due di
essi, potrebbe anche essere di lunghezza unitaria e quindi le terne possibili
salgono alle seguenti 20:
180·1·1
90·2·1
60·3·1
45·4·1
45·2·2
36·5·1
30·6·1
30·3·2
20·9·1
20·3·3
18·10·1
18·5·2
15·12·1
15·6·2
15·4·3
12·5·3
10·6·3
10·9·2
9·5·4
6·6·5
Ognuna di esse sarebbe potuta essere la soluzione giusta senza gli altri dati
forniti dall'insegnante. Onde sfoltire tale lista occorre allora tener conto
anche di questi ultimi, seppur incerti, controllando quali possibili terne
possono rientrare nei limiti imposti. Esaminiamo dapprima il dato che il
semiperimetro di base della torre è uguale alla lunghezza dell’aula in cui
sono presenti gli alunni, espressa in metri, tenendo conto che per ciascuna
terna di numeri interi su scritti non sappiamo quali sono le due misure che
rientrano fra i lati di base, ovvero in ogni terna qualsiasi dimensione può
essere rappresentativa dell'altezza del parallelepipedo e quindi tutte le terne
individuano tre possibili sottocasi, e che i ragazzi, che stanno risolvendo il
problema, conoscono, almeno approssimativamente, la lunghezza della loro aula,
ovvero è per loro un dato noto, quasi inconfutabile.
Nella terna 180·1·1 possiamo escludere che 180 metri sia l'altezza del
parallelepipedo, altrimenti l'aula sarebbe lunga solo due metri che è una
misura troppo piccola, incompatibile per le esigenze didattiche. Possiamo
escludere anche che sia alta un metro in quanto si otterrebbe un'aula
lunghissima di ben 181 metri, quando invece sappiamo che mediamente essa può
oscillare dai quattro ai nove metri al massimo. Per tale motivo eliminiamo
subito, senza indugi, la terna suddetta, e, per lo stesso motivo, anche le terne
90·2·1, 20·9·1, 18·10·1, 15·12·1, 10·9·2 e 6·6·5 in quanto in ogni
sottocaso darebbero aule troppo stette o troppo grandi e quindi inesistenti.
Restano da esaminare le restanti 13 terne:
60·3·1
45·4·1
45·2·2
36·5·1
30·6·1
30·3·2
20·3·3
18·5·2
15·6·2
15·4·3
12·5·3
10·6·3
9·5·4
Esaminiamo ora il dato che la somma di uno dei lati della base del
parallelepipedo con l’altezza di questa, espresse in metri, è uguale all’età
media degli alunni che devono risolvere il compito. Essendo questi del quinto
Liceo Scientifico la loro età media può, al massimo, variare da 17 a 20 anni,
considerando anche numerosissimi eventuali ripetenti. Anche in questo caso
occorre tener presente che tutte le terne rimaste individuano tre possibili
sottocasi in quanto qualsiasi misura può rientrare nel lato di base escluso dal
conteggio.
Nella terna 60·3·1 possiamo escludere che 60 metri sia un lato di base del
parallelepipedo, altrimenti l'aula sarebbe ancora troppo lunga, e quindi potrà
rappresentare solo la sua altezza, cosa che possiamo anche escludere in quanto
sommata ad una delle altre due misure darebbe un'età media degli alunni ai
limiti di un'età di pensionamento di vecchiaia (ben oltre i 60 anni)! Per tale
motivo eliminiamo anche la terna suddetta, e, per lo stesso motivo, anche le
terne 45·4·1, 45·2·2, 36·5·1, 30·6·1, 30·3·2, e 20·3·3 in quanto in
ogni caso darebbero alunni troppo anziani con un'età superiore ai prestabiliti
20 anni. Poichè nelle premesse del testo del problema si dice che gli alunni
sono tutti bravissimi e da sempre studenti modello, escludiamo anche
quest'ultima ipotesi, ovvero con numerosi ripetenti presenti, e quindi con
ragazzi di età media proprio uguale a 20 anni rappresentati nell'unica terna
18·5·2 Possiamo infine escludere anche le terne 10·6·3 e 9·5·4 visto che
in ogni sottocaso darebbe invece un'età media degli allievi al di sotto dei
prefissati 17 anni. Restano così da esaminare le seguenti tre terne sulle quali
tutti gli alunni non possono far altro che indugiare a lungo senza consegnare il
compito in quanto tutte equiprobabili:
15·6·2
15·4·3
12·5·3
di cui la prima misura di ciascun terna indica necessariamente l'altezza della
torre (altrimenti si avrebbero, al solito, aule troppo lunghe) e le restanti due
i lati della base. Se ne deduce che l'aula scolastica è lunga o sette metri (=
4 + 3) oppure otto metri (= 6 + 2 = 5 + 3), mentre l'età media degli alunni
risulta pari o a 17 anni (= 15 + 2 = 12 + 5), oppure 18 anni (= 15 + 3), od
infine 19 anni (= 15 + 4). Pertanto, ciascuno di essi, pur conoscendo
approssimativamente i due dati ricavati non riescono in prima battuta a
risolvere il problema in quanto i risultati sono molto prossimi tra loro. Ad
esempio non potendo effettuare direttamente le misure dell'aula non sanno, con
estrema precisione, se essa è lunga sette od otto metri, o magari è giusto un
bel rettangolo 7·8 metri quadri, od ancora ciascuno, pur conoscendo bene tutti
i propri compagni, resta indeciso sulle rispettive date di nascita che possono
far variare anche di una sola unità il valore medio delle loro età. Quindi
essi hanno bisogno necessariamente dell'ultimo dato: la semisomma dell’altezza
della torre con uno dei lati della base è uguale al numero delle mele che la
moglie del professore ha comprato al mercato il giorno precedente. I risultati
di tale calcolo producono per la terna 15·6·2:
(15 + 6)/2 = 21/2 = 10,5
(15 + 2)/2 = 17/2 = 8,5
entrambi impossibili perchè non interi; per la terna 15·4·3 invece producono:
(15 + 4)/2 = 19/2 = 9,5
(15 + 3)/2 = 18/2 = 9
il primo impossibile, il secondo accettabile; infine per la terna 12·5·3
risulta:
(12 + 5)/2 = 17/2 = 8,5
(12 + 3)/2 = 15/2 = 7,5
nuovamente entrambi impossibili. Resta pertanto solo la terna 15·4·3 da cui si
ricavano nove mele acquistate al mercato, corrispondenti a circa due chilogrammi
e quindi sufficienti per il fabbisogno di una famiglia, un'età media degli
alunni compresa fra i 18 (= 15 + 3) ed i 19 (= 15 + 4) anni, del tutto
verosimile per una classe di quinto Liceo Scientifico composta da studenti
modello, una lunghezza dell'aula pari a sette metri ed a un'area di base della
torre di esattamente 4·3 = 12 metri quadrati.
![]()
Sito Web realizzato da Gianfranco Bo