12 - INTERFEROMETRO DI FABRY-PEROT

In questo capitolo:

• 1 - Proprietà selettive dell'interferometro di Fabry-Perot

Indice – Glossario - Bibliografia - Elenco dei simboli - ï ñð

12.1 - Proprietà selettive dell'interferometro di Fabry-Perot

L'interferometro di Fabry-Perot è costituito da due specchi piani posti parallelamente tra loro; lo spazio racchiuso tra gli specchi costituisce la cosiddetta "cavità".

Ciascuno specchio è semiriflettente, cioè in parte riflette e in parte trasmette la luce incidente.

Per meglio comprenderne il funzionamento, supponiamo che ogni superficie rifletta il 90% e ne trasmetta il 10%. Quando un fascio di luce colpisce lo specchio anteriore, solo il 10% del fascio entra nella cavità.

Lo specchio posteriore ha le stesse proprietà di quello anteriore, quindi solo il 10% del fascio entrato nella cavità passerà all'esterno. Come risultato complessivo tale dispositivo trasmetterrà in uscita solo l' 1% della luce incidente.

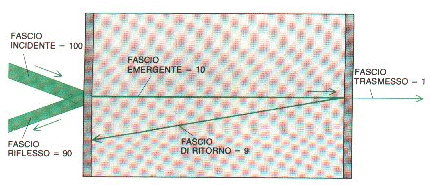
Fig. 12.1.1 - La figura evidenzia i fasci riflessi e trasmessi, in un Fabry-Perot, nel caso di riflettività al 90% degli specchi semiriflettenti che lo costituiscono.

Il fascio riflesso all'interno della cavità comincerà a "rimbalzare" all'interno della stessa, attenuandosi ad ogni passaggio e indebolendosi sempre più, fino ad esaurirsi; il contributo ulteriore al fascio trasmesso, ad ogni riflessione, è piccolo.

Nel fare queste considerazioni si è, però, trascurato un fatto importante.

La luce è composta di onde elettromagnetiche, e come tali sono in grado di sommarsi e di sottrarsi tra di loro, a seconda della fase relativa.

Consideriamo, per semplicità, solo il fascio incidente e quello di ritorno sul secondo specchio, all'interno della cavità.

Se le due onde sono in opposizione di fase, cioè i picchi dell'uno sono allineati con i ventri dell'altro, si ha interferenza "distruttiva" e l'onda risultante è data dalla differenza delle due.

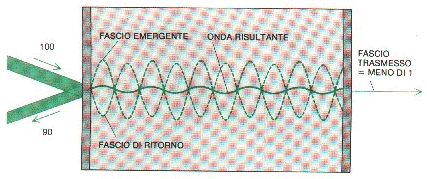
Fig. 12.1.2 - Condizioni di "interferenza distruttiva" all'interno di un Fabry-Perot. L'onda diretta e quella riflessa sono in opposizione di fase.

Se le due onde che si incontrano sono in fase, cioè i rispettivi picchi e ventri sono allineati, si ha interferenza "costruttiva" e l'onda risultante è data dalla somma delle due. Naturalmente saranno possibili situazioni intermedie.

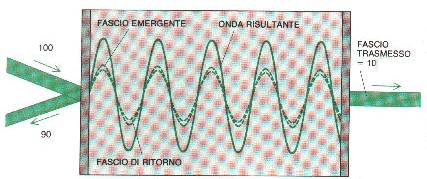
Fig. 12.1.3 - Condizioni di "interferenza costruttiva" all'interno di un Fabry-Perot. Le onde dirette e quelle riflesse sono in fase tra loro.

Quando l'interferenza è completamente "distruttiva", l'intensità della luce all'interno della cavità si annulla e altrettanto avviene per il fascio trasmesso.

Quando, al contrario, l'interferenza è "costruttiva", i fasci di andata e ritorno si rinforzano a vicenda, rendendo praticamente nulla la riflessione sul secondo specchio, e rendendo possibile la trasmissione di tutto il fascio esistente all'interno della cavità.

L'importanza dell'interferometro sta nel suo potere di selezionare le frequenze trasmesse, rispetto a quelle incidenti.

Per avere interferenza costruttiva occorre, infatti, che la luce all'interno della cavità, abbia una lunghezza d'onda l _n particolare; deve essere soddisfatta la seguente relazione:

L_c è la lunghezza della cavità.

E' evidente che solo certe lunghezze sono in "risonanza", come comunemente si dice, con la cavità, e possono essere trasmesse; le altre vengono eliminate.

Quanto affermato è giustificato dal fatto che nelle riflessione la luce viene ribaltata di fase e quindi si ha interferenza "costruttiva" solo se sulla parete la luce incide in corrispondenza di un nodo, cioè il punto intermedio tra un picco e un ventre.

La cavità di un Fabry-Perot ha la stessa funzione selettiva della cavità di un "laser" qualunque, nei quali il fascio laser emergente può essere solo quello in risonanza con la cavità; anche le funzioni d'onda all'interno di una buca di potenziale sono determinate con lo stesso principio.

Variando la lunghezza della cavità, o inserendo all'interno della cavità un materiale con un certo indice di rifrazione n_c , è possibile selezionare le lunghezze d'onda, e quindi le frequenze, da trasmettere.

Si ricorda che cambiare l'indice di rifrazione di un mezzo equivale a cambiare la lunghezza d'onda della luce al suo interno, visto che la frequenza non cambia; si ha, infatti:

v_n è la velocità della luce nel mezzo con indice di rifrazione n_c , c la velocità della luce nel vuoto e n_n la sua frequenza.

ï ñð