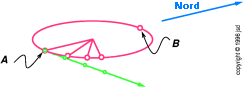
Figura 19.1: Oggetto in partenza dalla centrifuga
| Tradotto dal Gruppo SHIFTE-I | [Vittorio Urcioli ] |
| Versione 1.0 | 13 Marzo 2002 |
| Bozza | In corso aggiornamento link a figure ed altre pagine |
[Precedente] [Sommario] [Successivo]
[Commenti o domande]
Copyright © 1996-2001 jsd
Questo capitolo raccoglie alcuni concetti di fisica di base che vengono utilizzati in
vari passaggi di questo libro.
Approfondiremo in modo particolare il Moto Rotatorio, dato che questo è
generalmente meno familiare del Moto Rettilineo. In particolare, i Giroscopi si
comportano in modo molto diverso rispetto ad oggetti non rotanti. Ed è incredibile
quanto l’effetto giroscopico possa essere potente.
Prima di tutto, rivediamo le leggi fisiche che governano il moto rettilineo. Anche se i concetti basilari furono espressi da Galileo, parleremo delle Leggi di Newton, visto che fu Newton a codificare il fenomeno e a generalizzarne le applicazioni.
La Prima Legge del Moto dice: "Un corpo in quiete o in moto rettilineo uniforme
tende a rimanere in quiete o in moto rettilineo uniforme a meno che una forza esterna non
intervenga a modificare tale stato". Anche se questa potrebbe non sembrare una
affermazione degna di rilievo, è stata una delle rivoluzioni più profonde
della storia della scienza. Prima dei tempi di Galileo, le forze di attrito non venivano
considerate nella dinamica dei corpi. L’attrito era visto come "naturale" e
"scontato", cioè da non spiegare. La sola cosa che richiedeva spiegazioni era la
forza necessaria per vincere l’attrito in un corpo in moto rettilineo uniforme.
Galileo e Newton modificarono questo concetto. Da allora lo stato considerato "naturale"
divenne quello di assenza di attrito, e si iniziò a considerare e calcolare le
forze di attrito esattamente come tutte le altre forze.
La Seconda Legge del Moto dice: "Se un corpo subisce una qualunque variazione di
velocità (cioè una accelerazione), la forza richiesta (F) è
pari alla massa del corpo (m) moltiplicata moltiplicata per l’accelerazione
subita (a)". In simboli diventa:
Tenendo presente che si definisce Quantità di Moto (o Momemto) di un corpo il prodotto della sua massa per la sua velocità (e supponendo la massa costante), la Seconda Legge del Moto può essere così espressa: la Forza esercitata su di un corpo è pari alla variazione della sua Quantità di Moto (o Momento) nell’unità di tempo. Oppure, analogamente, la variazione di Quantità di Moto (o Momento) di un corpo è pari alla forza moltiplicata per il tempo.
La Terza Legge del Moto dice: "Se una forza viene applicata ad un corpo, il
corpo reagisce con una forza uguale e contraria". Anche questo principio può
essere espresso in termini di Quantità di Moto: se diamo una certa Quantità
di Moto ad un oggetto, dovremo dare una Quantità di Moto pari e opposta a
qualcos’altro. 1
Questo significa che la Quantità di Moto globale dell’universo non cambia.
Questo principio — conservazione della Quantità di Moto (o Momento) — è uno dei fondamenti della Fisica, al pari del
Principio di Conservazione dell’Energia discusso in capitolo 1.
Nonostante la semplicità di queste leggi, esse sono spesso male interpretate.
Ad esempio, c’è il diffuso convincimento che un aeroplano in una salita a
rateo costante richieda una maggior portanza, mentre una discesa a rateo costante una
portanza minore.2
Ricorda, la portanza è una forza e qualunque forza non bilanciata darebbe luogo
ad un’accelerazione, non ad un volo stazionario (cioè a rateo costante).
In un volo non accelerato (incluse salite e discese a rateo costante), le forze dirette verso l’alto (principalmente la portanza) devono equilibrare le forze dirette verso il basso (principalmente la forza peso). Se l’aeroplano è soggetto ad una forza verso l’alto non equilibrata, non salirebbe a velocità costante — ma verrebbe accelerato verso l’alto con una velocità verticale crescente.
Naturalmente, nella transizione tra volo livellato a salita a rateo costante, una forza verticale (relativamente debole) non equilibrata deve essere applicata temporaneamente. Una velocità di salita di 500 piedi/min corrisponde ad una componente verticale di velocità di soli 5 nodi, quindi la Quantità di Moto (o Momento) nella direzione verticale è relativamente bassa. L’energia cinetica nella direzione verticale è trascurabile.
Ad ogni modo, una volta che è stata ottenuto un assetto di salita a rateo costante, tutte le forze in gioco sono equilibrate.
Supponiamo che Moe sia posto su di una ampia e liscia tavola perfettamente rotante.
Moe ha anche dipinto su questa tavola un sistema di riferimento X, Y , in modo da
essere in grado di valutare la sua posizione, velocità ed accelerazione relativa
al suo sistema di riferimento rotante. Il suo amico Joe osserva i movimenti di Moe e li
misura rispetto ad un Sistema di Riferimento non-rotante.
|
Moe in breve tempo si rende conto che la Prima Legge di Newton non è applicabile in un Sistema di Riferimento rotante. Infatti, una pallina da tennis posta sulla tavola (ovunque eccetto che esattamente sul centro di rotazione), verrà centrifugata verso l’esterno. |
|
Nel Sistema di Riferimento non-rotante di Joe, non esistendo una forza centrifuga, la Legge di Newton è applicabile. |
|
Moe fissa la pallina alla tavola con un elastico. |
|
Joe vede lo stesso elastico e la stessa forza. L’allungamento dell’elastico è un’indice della forza esercitata. |
|
Moe dice che la pallina non è in movimento relativa al suo Sistema di Riferimento. L’elastico equilibra la forza centrifuga. |
|
Joe dice che la Quantità di moto (o Momento) della pallina cambia direzione in continuazione a causa della rotazione. L’elastico genera la forza necessaria. |
Adesso vedremo cosa succede ad un corpo in movimento relativo in un Sistema di Riferimento rotante.
Supponiamo che Moe fissi ad un’auto con un elastico un'altra pallina da tennis. Moe guida liberamente quest’auto mentre Joe osserva la pallina passare alcuni riferimenti (A, B, ecc) posti sulla tavola rotante.
|
Moe vede la pallina muoversi dal riferimento A al riferimento B. Naturalmente Moe vede i riferimenti fissi sulla tavola rotante. |
|
Joe conferma che la pallina si è spostata dal riferimento A al riferimento B, ma lui deve tener presente che i riferimenti stessi sono in movimento. |
Dal punto di vista "rotante" di Moe, possiamo dire:
I contributo #3 è numericamente uguale al contributo #4. L’effetto finale
è perfettamente analogo ed entrambi questi contributi vengono chiamati Effetto
di Coriolis.3
L’Effetto di Coriolis può essere descritto come
un’accelerazione (proporzionale alla velocità dell’oggetto), ed
analogamente può essere descritto come una forza (proporzionale al momento
dell’oggetto).
Consideriamo un riferimento posto su di un pianeta in rotazione verso Est come la Terra.
Nei paraggi del Polo Nord, l’accelerazione di Coriolis è sempre rivolta
verso destra, se si è orientati nel verso del moto. Uno spostamento verso Nord
provoca una accelerazione di Coriolis diretta verso Est, e quindi è necessario
opporre una forza verso Ovest se si vuole seguire una linea rettilinea verniciata sulla
Terra. Analogamente, uno spostamento verso Est provoca una accelerazione di Coriolis
verso Sud, ed è quindi necessario opporre una forza diretta verso Nord.
L’effetto di Coriolis si applica solo nel caso di moto sul piano di rotazione.
Nel caso di moto parallelo all’asse di rotazione, l’effetto di Coriolis non
è applicabile. In tutti i casi, l’accelerazione di Coriolis giace sul piano
di rotazione in direzione perpendicolare al moto.
Nei paraggi dell’equatore, bisogna fare attenzione dato che il piano di rotazione
non è orizzontale. In questa regione, uno spostamento verso Est provoca una
accelerazione di Coriolis rivolta verso l’alto, mentre uno spostamento verso Ovest
provoca una accelerazione di Coriolis rivolta verso il basso. In questa regione,
spostamenti in direzione Nord/Sud sono paralleli all’asse di rotazione e quindi non
provocano alcun effetto di Coriolis.
Per riassumere: l’effetto di Coriolis e le forze centrifughe sono due contributi
distinti. L’effetto di Coriolis si applica solo agli oggetti in movimento relativo
in un sistemo di riferimento rotante. Le forze centrifughe interessano tutti gli oggetti
posti in un sistema rotante, sia che questi siano in quiete o in movimento.
Supponiamo di essere in un aeroplano in volo rettilineo a 120 nodi di velocità,
lungo il percorso più breve tra due punti della superficie terrestre. A causa
della rotazione della Terra, l’aereo sarà soggetto ad una accelerazione di
Coriolis di intensità pari a circa 0.001G. Questa accelerazione è
troppo piccola per essere misurabile o avvertibile.
Supponiamo adesso di trovarci a 60 piedi di distanza da un amico, giocando a pallone
all’interno del vano di carico di un aereo Cargo in virata a rateo costante di
3°/sec. Se l’amico ci tirasse la palla a 60 mph, questa sarà soggetta ad
una accelerazione di Coriolis maggiore di 0,25 G. Ciò significa che la
palla devierà lateralmente di circa 2 piedi — abbastanza per essere
apprezzato. In condizioni di volo ordinarie, comunque, non è lanciarsi oggetti a
distanze tali da generare effetti di Coriolis apprezzabili.
Il vento, nel suo moto relativo alla Terra, è soggetto ad una accelerazione di
Coriolis piccola ma costante. L’effetto risultante è terribilmente
importante, come discusso nel paragrafo 20.1.
Un aeroplano in virata, soprattutto se accentuata, si comporta come una centrifuga. Ci
sono profonde analogie tra il Campo delle Forze Centrifughe ed il Campo delle Forze
Gravitazionali:
|
Il Campo Gravitazionale è una accelerazione che viene applicata in ogni suo punto. Agisce su tutti i corpi con una forza proporzionale alla loro massa. |
|
Il Campo Centrifugo è anch’esso una accelerazione che viene applicata in ogni suo punto. Anch’esso agisce su tutti i corpi con una forza proporzionale alla loro massa. |
|
Il mio laboratorio non è un riferimento in caduta libera. Le stelle mostrano che è la Terra a spingere sulle sue fondamenta. Prendendo come riferimento le sue pareti, potremmo valutare l’accelerazione di gravità. |
|
Analogamente, l’interno di una centrifuga non è un riferimento inerziale. Anche in questo caso, prendendo come riferimento le sue pareti, potremo apprezzare l’accelerazione gravitazionale. |
Per meglio comprendere l’equilibrio delle forze agenti in un aereo in virata e/o
derapata, prendiamo in esame la centrifuga mostrata in figura 19.1. Per ora,
trascureremo l’effetto della gravità; immaginiamo che questa centrifuga
operi in un ambiente senza peso oppure su di una stazione orbitante. Supponiamo di avere
un osservatore all’interno della centrifuga, mostrata in rosso, e che questo lasci
andare una pallina da tennis verde quando transita per il punto A (il punto
più basso della nostra traiettoria). La pallina volerà via libera, mentre
l’osservatore proseguirà il suo moto circolare.
Capito il fenomeno base, vediamo cosa succede quando la centrifuga opera nel campo
gravitazionale della Terra. Questo è mostrati in figura 19.2. Quando la pallina
lascia la centrifuga, essa si muove ancora verso destra, ma adesso viene anche accelerata
verso il basso dalla forza di gravità.
Esaminiamo adesso le forze avvertite dal pilota di un aeroplano in virata. Iniziamo
con il caso di una virata coordinata, come mostrato in figura 19.3.
La definizione di derapata, imbardata e rollio è mostrata in figura 19.9.
|
Terminologia di questo libro |
|
Vecchia Terminologia |
|
|
|
|
|
asse di beccheggio |
|
asse trasversale |
|
stabilità sull’asse di beccheggio |
|
stabilità longitudinale |
|
asse di rollio |
|
asse longitudinale |
|
stabilità sull’asse di rollio |
|
stabilità laterale |
|
asse di imbardata |
|
asse verticale |
|
stabilità sull’asse di imbardata |
|
stabilità direzionale |
Il termine assetto descrive l’orientamento degli assi dell’aereo
rispetto alla Terra. L’assetto è definito da tre angoli: l’angolo di
prua, l’angolo di assetto e l’angolo di inclinazione.
Per posizionare l’aereo in un determinato assetto, partendo da un aereo in volo
livellato (cioè con gli assi X e Y orizzontali) e con la prua
rivolta a Nord. Quindi:
Come discusso in seguito (sezione 19.6.4), è importante operare queste rotazioni
nell’ordine specificato.
Abbiamo visto come, dato un set di tre angoli, sia possibile definire l’assetto di
un aeroplano. Adesso consideriamo il caso inverso: dato l’assetto di un aeroplano,
come si determinano i tre angoli che descrivono tale assetto?
Risposta: immaginate semplicemente di riportare l’aeroplano in un assetto di volo
livellato e diretto a Nord. Le rotazioni devono essere effettuate nell’ordine
inverso a quello specificato in precedenza:
La seguente tabella riassume i nomi e verbi relativi agli angoli ed alle rotazioni
attorno ai tre assi.
|
asse Z |
asse Y |
asse X |
|
|
Rotazione |
imbardata |
beccheggio |
rollio |
|
Angolo |
prua |
assetto |
inclinazione |
L’angolo di attacco è l’angolo tra la proiezione sul piano
XZ del vento relativo e l’asse X dell’aeroplano (o un altro
riferimento opportuno).
L’angolo di scivolata è l’angolo tra la proiezione sul piano
XY del vento relativo e l’asse X dell’aeroplano.
Alcuni testi di aerodinamica adottano il termine angolo di scivolata laterale.
Ciò potrebbe causare della confusione perché i testi di pilotaggio avanzato
fanno distinzione tra scivolata in avanti e scivolata laterale (anche se
tra le due non c’è alcuna differenza) come discusso con figura 11.1.
E’ una verità della geometria il fatto che la somma di una serie di
rotazioni dipende dall’ordine in cui queste rotazioni sono effettuate.
E’ da dire che in una serie di movimenti non rotatori, l’ordine non conta.
Infatti, supponiamo di avere due oggetti che, partendo dallo stesso punto, vengano
spostati. Spostiamo il primo oggetto prima di 2m verso Nord e poi 3m verso Ovest. Quindi
operiamo sul secondo oggetto gli stessi spostamenti ma in ordine inverso, cioè
prima 3m verso Ovest e poi 2m verso Nord. Se non ci sono ostacoli, i due oggetti si
troveranno nel medesimo posto. L’ordine con cui ho effettuato questi spostamenti
non è influente sul risultato finale.
Gli angoli, invece, non seguono le stesse regole delle distanze. Per esempio, è
possibile variare la prua, per esempio di 37°, anche senza virare. Ci sono due
modi:
Se l’aereo (ed i suoi occupanti) può sopportare elevati carichi, queste
manovre sono assolutamente accettabili per operare virate strette ad alta
velocità.
Per aerei non-acrobatici, va applicata una definizione più moderata: una
rotazione nel piano orizzontale non è una pura imbardata se l’aereo
non è in assetto orizzontale (cioè con assetto ed inclinazione nulli). Per
esempio, supponiamo di essere in volo livellato durante una virata a sinistra.
Ciò significa che l’aereo sta rotando attorno al suo asse di imbardata, che
è diretto verso il centro della Terra. Supponiamo adesso di essere in volo
livellato, ma con un angolo di assetto non nullo, ma positivo. Ciò
significa che l’asse di imbardata non è più verticale. In questo
caso, sarebbe possibile effettuare la virata livellando l’assetto abbassando il
muso, imbardando dell’angolo richiesto ed infine rialzando il muso
all’assetto originario. Ma dato che le rotazioni non sono sommabili, operando solo
una imbardata senza livellare prima l’assetto porterebbe alla necessità di
livellare le ali con un leggero rollio in senso orario.
Queste considerazioni sono esatte al 100%, ma totalmente irrilevanti durante il normale
pilotaggio. 5 In particolare, la rotazione attorno all’asse
di rollio non porta a modifiche degli angoli di attacco delle due ali. Discutere sul
fatto che una variazione di prua sia una pura imbardata oppure una composizione di
imbardata e rollio, è come discutere sul bicchiere d’acqua mezzo vuoto o
mezzo pieno — in realtà sono la stessa cosa. In questo caso, la
realtà è semplice: l’ala interna (sinistra) segue na traiettoria
circolare orizzontale, mentre quella esterna (destra) segue anch’essa una
traiettoria circolare orizzontale ma leggermente più lunga.
E’ facile capire il perché: la virata richiede una rotazione attorno
all’asse verticale. Tale rotazione muove tutto orizzontalmente, e quindi possono
cambiare le velocità ma non gli angoli di attacco flusso che investe le due
ali.
Supponiamo adesso di effettuare una virata a sinistra
durante una salita.
Supponiamo anche che l’asse di imbardata sia perpendicolare alla direzione del
volo, l’asse di beccheggio orizzontale e l’asse di rollio parallelo alla
direzione di volo, cioè senza scivolata.
Durante la virata in volo livellato, la prua dell’aereo cambia. E’ una
rotazione attorno ad un asse perfettamente verticale. Durante una salita, l’asse di
imbardata non è più verticale, quindi la virata non è più una
semplice imbardata. La virata infatti porta adesso l’ala interna a spostarsi verso
dietro ed in basso. Quindi per variare la prua mantenendo l’assetto e
l’inclinazione invariati, dovrò combinare una imbardata a sinistra con un
rollio verso destra, in senso orario.
Questo rollio è dovuto al fatto che (a parità di condizioni) l’ala
esterna volerebbe con un angolo di attacco inferiore durante una virata in salita, e che
quindi produrrebbe meno portanza. Di conseguenza è necessario compensare la
portanza delle ali tramite gli alettoni.
Si è detto "produrrebbe" e non "produce" perché, bilanciando con gli
alettoni, entrambe le ali di fatto producono la stessa portanza. Infatti, a causa del
movimento di rollio, l’aria investe le due ali con angoli attacco diversi. Gli
alettoni sono quindi utilizzati non per creare una differenza di portanza, ma per evitare
che venga creata una differenza di portanza.
Anche se il valore della portanza resta invariato, la sua direzione è mutata,
come discusso in sezione 8.8.4; in particolare figura 8.7. Dovremo usare il timone per compensare la
tendenza all’imbardata: pedaliera a destra per barra a destra, pedaliera a sinistra
per barra a sinistra.
In una virata in salita, l’effetto della differenza di direzione del flusso
d’aria che investe le due ali si somma alla differente velocità delle due
ali, creando una forte tendenza al rollio della medesima direzione della virata. Nel caso
di una virata in discesa, l’effetto della differenza di direzione del flusso
d’aria si oppone all’effetto delle velocità. In vite, la differenza
delle velocità è un fattore fondamentale, come discusso in sezione 18.6.1, ed in
figura 18.6. Anche la
sezione 9.7 analizza le virate in salita ed in discesa in
termini leggermente diversi, facendo un esempio numerico.
Come detto nel paragrafo precedente, una rotazione nel piano orizzontale non è
una semplice imbardata se l’aereo non è in assetto orizzontale. Nel
paragrafo precedente abbiamo valutato le conseguenze nel caso di assetto non orizzontale,
ma la stessa logica può essere applicata anche al caso di inclinazione non
livellata. Questo caso è in un certo senso più rilevante, dato che
normalmente una virata porta ad una variazione di inclinazione, più che di
assetto.
Si potrebbe effettuare la virata richiesta portando a zero l’inclinazione,
operando una pura imbardata ed infine riportando l’inclinazione al valore di
partenza. Questo processo non è equivalente all’operare una pura imbardata
mantenendo l’inclinazione costante. Per piccoli angoli di inclinazione, la virata
ad inclinazione costante è principalmente una pura imbardata, ma
richiederà anche una rotazione attorno all’asse di beccheggio. A causa di
questo beccheggio, il vento relativo investe le ali e ed il timone ad angolazioni
diverse. Sarà necessario tirare leggermente la barra per compensare. Questa
trazione è da sommare alla trazione che sarà necessaria per controllare la
velocità durante la virata. I due fenomeni sono nettamente distinti: supponiamo di
mantenere un assetto costante durante la virata, in modo da ottenere l’incremento
di portanza necessario con un incremento di velocità piuttosto che con un
incremento dell’angolo di attacco. Sarà ancora necessario applicare un
po’ di trazione alla barra, per la non sovrapponibilità delle rotazioni.
Come la Prima Legge di Newton dice che per mettere in moto un oggetto bisogna
applicare una forza, c’è una legge analoga che dice che per mettere in
rotazione un oggetto è necessaria una coppia.
Potreste aver già sentito parlare di "coppia" in relazione alla tendenza a tirare
verso destra degli aerei in decollo, e potreste aver sentito la parola "momento" in
relazione a problemi di pesi e bilanciamenti. In effetti, "coppia" e "momento" sono due
nomi di una stessa cosa. In particolare,
Un esempio: il carburante ed il carico causano un momento di beccheggio che dipende
dal loro posizionamento longitudinale. Analogamente, genereranno un momento di rollio se
saranno caricati asimmetricamente verso destra o verso sinistra.
Un altro esempio: gli effetti giroscopici possono generare una coppia attorno
all’asse di imbardata . Allo stesso modo, essi possono causare una coppia attorno
all’asse di beccheggio.
I termini "coppia" e "momento" vengono quindi usati indifferentemente.
La coppia non è una forza. Delle due, il concetto di forza ci è più
familiare perché è ciò che riusciamo ad esercitare con una semplice
spinta o trazione. La forza si misura in Newton o Libbre (N o lb).
Per applicare una coppia, abbiamo bisogno di una forza e di una leva. La coppia è
calcolata dalla seguente formula:
coppia
Dove per braccio di leva si intende la distanza tra la retta di azione della
forza ed il centro di rotazione 6.
La coppia si misura in Newton x metro8 (Nm), oppure in Libbre x piedi (ftLb). Figura 19.10 mostra una
situazione in cui tutte le forze e coppie sono bilanciate. Infatti, sulla destra della
barra agiscono tre molle per 30 Libbre complessive. Sulla sinistra, ci sono due molle da
20 Libbre ognuna ed una terza molla da 10 Libbre. La somma delle forze agenti verso
destra bilancia la somma delle forze agenti verso sinistra.
Il concetto di momento angolare è fondamentale per la comprensione degli
oggetti rotanti.
Il momento angolare sta al momento come la coppia sta alla forza. Riassumendo le
analogie:
|
Moto rettilineo |
|
Moto angolare |
|
Forza |
|
Coppia (forza x braccio di leva) |
|
Momento |
|
Momento angolare (momento x braccio di leva) |
|
Il momento di un sistema non cambia a meno di applicare una forza. |
|
Il momento angolare di un sistema non cambia a meno di applicare una coppia. |
|
La variazione di momento di un sistema è pari alla forza per il tempo di applicazione della forza stessa. |
|
La variazione di momento angolare di un sistema è pari alla coppia per il tempo di applicazione della coppia stessa. |
Una forza applicata ad ogni oggetto comune porterà ad uno spostamento nella
direzione della forza. Si è talmente abituati a questo fenomeno che si tende a
dimenticare che forza e spostamento non sono esattamente la stessa cosa, e che non sono
sempre collegati.
Nel caso del giroscopio, ad esempio, se si applica una coppia attorno ad un asse, esso
risponderà con uno spostamento attorno ad un altro asse. Nel corso delle mie
lezioni su "See How It Flies", mi porto dietro una ruota di bicicletta con le manopole,
come quella mostrata in figura 19.13. Il senso di rotazione indicato corrisponde al comune senso di
rotazione dei motori ad elica americani, quando il muso dell’aereo è diretto
verso la sinistra del diagramma.
Ora che sappiamo che una coppia di beccheggio genera un’imbardata, potremmo
chiederci "in quale direzione?". L’imbardata sarà verso destra oppure verso
sinistra? Esiste una semplice regola: l’asse di applicazione della coppia
precederà di 90° l’asse della rotazione.9 Un esempio
di applicazione di questa regola è mostrato in figura 19.15.
|
La Coppia applicata precede di 90° la Rotazione. |
La precessione, e tutti gli altri effetti giroscopici discussi in questa sezione, sono
diretta conseguenza delle leggi del momento angolare discusse nella sezione
precedente.
Consideriamo adesso cosa succede quando un giroscopio non è soggetto a coppie
di rilievo.
Supponiamo di sospendere un giroscopio con una sospensione cardanica. La sospensione
cardanica supporterà il suo peso, ma non gli trasmetterà alcuna coppia,
anche se l’aereo su cui questa sospensione cardanica è installata dovesse
virare. Lo chiameremo un giroscopio libero, dato che è libero di non rotare
con l’aereo.
Anche un piccolo giroscopio può avere un enorme momento angolare, se la sua
velocità di rotazione è sufficiente. Ogni piccola coppia ad esso applicata
(a causa delle immancabili imperfezioni della sospensione cardanica), nel tempo
potrà variare il suo momento angolare — ma in un tempo ragionevolmente
breve, la variazione sarà trascurabile rispetto al momento angolare totale.
In tale situazione, il giroscopio tenderà a
mantenere lo stesso orientamento spaziale. Diremo quindi che il giroscopio è una
piattaforma inerziale rispetto alle rotazioni.11 Altri libri
dicono che il giroscopio mostra una rigidità spaziale, ma questa è
una strana espressione.
Adesso vedremo i principi di funzionamento dei tre strumenti giroscopici:
l’orizzonte artificiale giroscopico (indicatore di assetto), il giroscopio
direzionale (indicatore di prua), e l’indicatore di virata giroscopico (indicatore
di virata o coordinatore di virata).
Il giroscopio direzionale è un
giroscopio libero. E’ quindi una piattaforma inerziale.
Il giroscopio ruota in un piano verticale, quindi il vettore momento angolare è
diretto in una qualunque direzione orizzontale. Un sistema di ingranaggi misura
l’orientamento di tale vettore nel piano XY 12 e lo mostra
al pilota. Ila difficoltà è nel misurare l’angolo mentre si supporta
il giroscopio minimizzando le coppie accidentali agenti su di esso. Imperfezioni del
meccanismo porteranno una precessione del giroscopio. Quindi periodicamente sarà
necessario verificare e correggere l’indicatore di prua, tipicamente utilizzando
come riferimento una bussola magnetica.
L’orizzonte artificiale (detto anche misuratore d’assetto) è
un altro giroscopio libero. L’asse di rotazione del giroscopio è
orizzontale, quindi il suo vettore momento angolare è verticale. Un sistema di
ingranaggi misura l’angolo tra questo vettore ed i piani YZ (inclinazione) e
XZ (assetto), e li mostra al pilota.
E’ interessante paragonare l’orizzonte giroscopico (che ci dice in quale
direzione è "basso") con l’inclinometro a sfera o con il filo a piombo (che
mostrano una diversa interpretazione della direzione "basso"). La differenza consiste nel
fatto che il filo a piombo ci indica la direzione E-down, mentre il giroscopio è
progettato per indicarci la direzione N-down, cioè in quale direzione sia in
centro della Terra. Ogniqualvolta l’aeroplano è soggetto ad una
accelerazione (ad esempio durante la rotazione al decollo o durante una virata), le due
indicazioni sono molto diverse. Come mostrato in figura 19.17, in virata il vettore E-down viene centrifugato
verso l’esterno, mentre il vettore N-down è sempre dietto verso il centro
della Terra.
Se mediamo queste piccole deviazioni sull’arco di un intero giro, esse si
cancellano.
Naturalmente, se si compie una virata non completa, la somma delle deviazioni non
è più nulla, e l’indicatore di assetto sarà impreciso per un
certo tempo. Un errore analogo avviene durante il decollo, perché la stima che il
giroscopio fa del "basso" viene deviata verso dietro dall’accelerazione, e di
conseguenza la posizione dell’orizzonte artificiale sarà un po’ sotto
l’orizzonte reale per un po’ di tempo. Il tempo di elaborazione dello
strumento tipo è di circa cinque minuti. Quando gli strumenti invecchiano, il la
loro memoria si abbrevia, a causa del rallentamento del giroscopio, e quindi
l’errore aumenta.
Ci sono due tipi di indicatori di virata giroscopici: (a) il virometro, e (b)
il coordinatore di virata, o viro-sbandometro.
In entrambi i casi, il giroscopio non è libero; è un giroscopio
differenziale. Ciò significa che il suo asse di rotazione è fissato
sull’aereo, senza la sospensione cardanica. Quindi cambia il suo orientamento
quando l’aereo si imbarda, cioè rota attorno all’asse Z.13 Lo strumento misura la coppia necessaria per questa
variazione di orientamento.
A volte il virometro viene montato con il suo asse parallelo all’asse Y,
nel qual caso l’imbardata dell’aereo richiederà una coppia attorno
all’asse X. Altri modelli hanno l’asse di rotazione nella direzione
dell’asse X, nel qual caso un’imbardata richiederà una coppia
attorno all’asse Y. In principio, potrebbe essere utilizzata qualunque
coppia di assi del piano XY.14
La coppia necessaria è proporzionale a (a) la velocità di variazione della
prua, e (b) il momento angolare del giroscopio. Quindi un accurato virometro deve rotare
rigorosamente alla velocità "di progetto", né troppo piano né troppo
forte (questo è in contrasto con il giroscopio direzionale e l’orizzonte
artificiale giroscopico, dove il giroscopio deve semplicemente girare "abbastanza"
velocemente).
Molti giroscopi differenziali usano uno stratagemma. Sono in rotazione sull’asse
Y, con la parte alta del giroscopio in rotazione verso il retro. Quindi, la
direzione del vettore momento angolare è nella direzione + Y. Una piccola
molla permette una piccola precessione del giroscopio attorno all’asse X. In
una virata a sinistra, la precessione sposterà leggermente a destra. Ciò
significa che durante la virata lo spostamento dell’asse del giroscopio annulla in
un qual modo l’inclinazione dell’aereo, lasciando l’asse del giroscopio
più allineato con l’asse polare terrestre. Lo scopo è quello di
creare uno strumento capace di misurare direttamente le variazioni di prua (rispetto
all’asse polare della Terra), piuttosto che la semplice rotazione attorno
all’asse Z dell’aereo. Siccome la relazione tra inclinazione e
velocità di virata dipende dalla velocità del velivolo, dal fattore di
carico, et cetera, questo stratagemma non può raggiungere lo scopo a meno che in
alcuni casi particolari.
Il coordinatore di virata è molto simile al
virometro. Esso mostra la sagoma di un aereo invece di una lancetta. La differenza
principale è il coordinatore di virata è sensibile sia alla velocità
di rollio che alla velocità di virata. Per realizzare tale strumento, è
sufficiente inclinare un virometro alzandone il muso di 20-30°, e cambiare il
quadrante.
Il vantaggio del coordinatore di virata è che ci aiuta ad anticipare le azioni
necessarie in virata. Per esempio, se l’aereo ha le ali livellate ma si sta
inclinando verso destra, probabilmente inizierà presto a virare verso destra, e
quindi potremmo recuperare prontamente l’equilibrio lavorando di alettoni. Lo
svantaggio di questo strumento si ha in turbolenza. Le turbolenze spesso portano
l’aereo ad inclinarsi continuamente verso destra e verso sinistra. La
velocità di rollio può essere rilevante, anche se non si raggiungono mai
angoli di inclinazione molto ampi. Le turbolenze hanno un effetto minore sull’asse
di imbardata. In tali condizioni, un normale virometro fornisce una indicazione
più stabile ed affidabile del coordinatore di virata.
Sfortunatamente il quadro del coordinatore di virata mostra la sagoma di un aereo che si
inclina a destra o a sinistra. Questo porta alcuni a credere erroneamente che lo
strumento indichi l’angolo di inclinazione, il che è decisamente
sbagliato.
[Precedente] [Sommario] [Successivo]
[Commenti o domande]
Copyright © 1996-2001 jsd