
figura 3.1: Flusso attorno all'ala
| Tradotto dal Gruppo SHIFTE-I | [ Carlo Traverso (travc@libero.it)] |
| DA FARE |
Verifica tutti i link; rilettura e controllo punteggiatura. Piccola traduzione in una nota |
| Versione 1.2 | 16 Agosto 2002 |
| Nomi del tipo {@default###} |
|
| Link Capitoli/Sezioni/Figure/Note |
|
[Precedente] [Sommario] [Successivo]
[Commenti o domande]
Copyright © 1996-2001 jsd
In questo capitolo vedrò di spiegare due o tre cose su come si comporta l'aria quando passa su un'ala . Ci saranno molte illustrazioni, del tipo figura 3.1, ottenute con un programma di simulazione del tunnel del vento che1 che ho scritto per il mio computer. L'ala è ferma nella galleria a vento; l'aria fluisce su di essa da sinistra verso destra. Un po' sopravvento all'ala (vicino al lato sinistro del disegno ) è sistemata un fila di iniettori di fumo. Sette di essi, che iniettano del fumo rosso, sono in funzione continuamente. Il fumo viene trasportato dalla corrente rendendo visibili le linee di flusso.

figura 3.1: Flusso
attorno all'ala
Inoltre, con una spaziatura verticale sette volte più fitta, sono piazzati degli iniettori pulsanti che emettono fumo per 10 millisecondi, e per altri 10 millisecondi restano spenti. In figura, il fumo blu è stato iniettato da 70 millisecondi, il verde da 50, l'arancione da 30 e il rosso ha iniziato a essere iniettato da 10 millicecondi. L'iniezione del fumo rosso sta giusto terminando nel momento in cui è stata presa l'immagine.
L'insieme di tutti i punti che sono "usciti" dgli iniettori in un determinato istante va a formare una timeline. Il bordo destro della striscia di fumo arancione, ad esempio, è la "timeline" dei 30 msec.
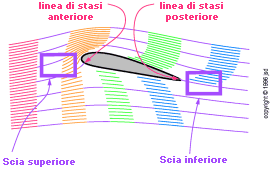
figura 3.2:
Upwash e Downwash
La figura 3.2 evidenzia alcune importanti proprietà dei modelli di flusso aerodinamici. Innanzitutto possiamo notare che l'aria davanti all'ala non si muove solo da sinistra a destra, ma anche dal basso verso l'alto; questo fenomeno viene detto upwash (deviazione verso l'alto, n.d.t.). Allo stesso modo, una volta oltrepassata l'ala, l'aria si muove, oltre che verso destra, anche verso il basso; e questo viene detto downwash (deviazione verso il basso,n.d.t.). Il downwash dietro l'ala è relativamente facile da capire; scopo dell'ala è in fondo quello di imprimere un qualche movimento verso il basso all'aria.
L' upwash davanti all'ala è un po' più interessante. Come già discusso nella sezione 3.6, l'aria è un fluido, il che significa che essa può esercitare pressione su se stessa come sugli altri oggetti. La pressione dell'aria agisce energicamente sull'aria stessa, anche su quella davanti all'ala.
Lungo il bordo d'entrata dell'ala c'è una cosa chiamata linea di ristagno, che è la linea di divisione fra l'aria che passa sopra l'ala e quella che passa sotto. Su un aereo, la linea di ristagno corre per tutta l'apertura alare, ma dato che la figura 3.2 mostra solo una sezione trasversale dell'ala, quello che si vede è un singolo punto.
Un' altra linea di ristagno corre lungo tutto il bordo di uscita. Essa indica il luogo in cui l'aria passata sopre l'ala si ricongiunge con quella passata sotto.
Si vede che per angoli di attacco medio alti, la linea di ristagno anteriore si trova ben sotto e dietro del bordo d'entrata dell'ala. L'aria che incontra l'ala appena sopra la linea di ristagno sarà respinta verso il muso dell'aereo, fluirà verso l'alto sul bordo d'entrata e quindi verso l'indietro lungo il dorso dell'ala.
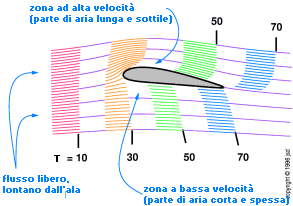
figura 3.3:
Campo delle velocità nei pressi di un'ala
La figura 3.3 introduce alcuni ulteriori utili concetti. Dato che l'aria, nei pressi dell'ala scorre nelle più varie direzioni e con differenti velocità, sorge la domanda su qual'è la "vera" velocità dell'aria nel tunnel. La cosa logica da fare è misurare la velocità della corrente libera; che si può rilevare in un punto ben a monte, prima che il flusso venga disturbato dall'ala.
I filetti di fumo pulsanti ci danno molte altre informazioni. Le zone dove i filetti appaiono allungati sono zone di alta velocità. Questo è facile da vedere; ogni striscia (piena o vuota) dura esattomente 10 millisecondi, per cui se copre una distanza maggiore deve muoversi più velocemente. La massima velocità prodotta da questa ala a questo angolo di incidenza è circa due volte la velocità della corrente libera . I profili alari sono molto efficaci per accelerare l'aria.
Per contro, le zone dove i filetti pulsanti coprono una distanza minore nei 10 millisecondi, devono essere zone di bassa velocità. La velocità minima è zero, e questo si verifica davanti e dietro le linee di ristagno.
Il vento relativo si annulla sulle linee di ristagno. Un qualunque moscerino che passeggia sull'ala di un aereo in volo, se cammina sulla linea di ristagno non sentirà alcun vento.2
Le linee di flusso hanno una notevole proprietà : l'aria non le può mai attraversare. Ciò è dovuto al modo in cui le linee di flusso sono state definite: con il fumo. Se dell'aria volesse passare in un punto dove c'è il fumo, lo trascinerebbe con se. Ne consegue che una determinata porzione di aria, compresa fra due linee di flusso e due "timeline" non perde mai la sua "identità". Può cambiare forma, ma non può mescolarsi con un'altra porzione definita con gli stessi criteri.3
Un'altra cosa che dovremmo notare nelle zone di bassa velocità, è che le linee di flusso sono più spaziate fra loro. Questo non a caso. A velocità "ragionevoli" l'ala non "comprime" o "decomprime" l'aria in maniera così forte da farle cambiare densità in modo significativo (vedi sezione 3.4.3 per approfondimento). Conseguenza di questo fatto, le porzioni di aria precedentemente definite non cambiano la loro area quando cambiano di forma. In una certa zona avremo le porzioni di aria strette e allungate che passano per un certo punto ad alte velocità. (Se la stessa quantità di fluido attraversa un'area minore, deve aver velocità maggiore) In un'altra zona avremo porzioni corte e larghe che passano a bassa velocità.
La cosa più degna di attenzione in questa figura è che il fumo blu che passa (stretto e veloce) sul dorso dell'ala, raggiunge il bordo di uscita circa 10 -15 millisecondi prima del corrispondente che è passato sotto l'ala.
Questo non è un errore. In verità vedremo in sezione 3.10.3 che se ciò non fosse vero, l'ala non potrebbe generare portanza.
Questo fatto potrà essere shockante per molti lettori, a causa di tutti quei richiami a riferimenti standard che pretendono che l'aria debba passare sopra e sotto l'ala nello stesso intervallo di tempo. Ho visto questa errata affermazione in libri di testo elementari, testi di fisica, enciclopedie e ben noti manuali per piloti. Seguitemi un momento, e vi convincerò che la figura 3.3 racconta le cose come stanno.
Per prima cosa, devo convicervi che non c'è nessuna legge fisica che vieti a un particella di fluido di essere in ritardo rispetto a un'altra.
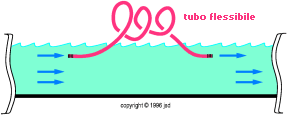
figura 3.4: il Ritardo Non
è Proibito
Consideriamo la situazione descritta in fig. figura 3.4.Un fiume (di acqua) scorre da sinistra a destra. Utilizzando un pezzo di manichetta, aspiro dell'acqua dal fiume, la faccio scorrere attraverso alcune spire di manichetta arrotolata, e quindi la faccio ritornare nel fiume. L'acqua che passa attraverso la manichetta sarà ritardata. La particella d'acqua ritardata non si ricongiungerà con quelle che le erano vicine prima di entrare nella manichetta, e nemmeno proverà a riuscirci.
Si noti che il ritardare l'acqua non richiede di comprimerla, nè richiede attrito.
La stessa storia si applica all'aria.L'aria che passa attorno a un ostacolo viene ritardata. In effetti, basta che l'aria arrivi abbastanza vicina alla linea di ristagno perchè sia ritardata per tutto il tempo che si vuole. Le molecole d'aria che stanno sulla linea di ristagno, si comportano come l'asino di Buridano, incapace di decidersi tra i due sacchi di biada, non sapendo decidere quale strada scegliere. Questo ritardo si ha anche quando l'ala non genera portanza, come è mostrato nel quadro in alto di figura 3.5.
Si può vedere ciò in tutti i casi in cui l'aria che "colpisce" la linea di ristagno muore lì (il filetto blu centrale) e non arriva al bordo d'uscita in nessuna di queste figura.
Quando un'ala non produce portanza4 essa costituisce solo un sottile ostacolo al flusso aereo. L'aria che passa vicino all'ala viene leggermente ritardata, ma questo è tutto. L'aria che scorre sopra l'ala è ritardata nellla stessa misura di quella che scorre sotto.
Quando invece l'ala genera portanza, gli andamenti del flusso diventato assai più interessanti, come si può vedere dalle altre figura di figura 3.5.
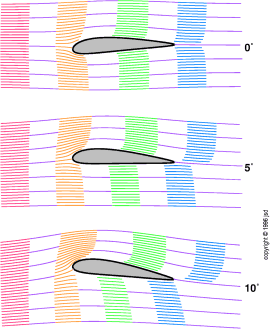
figura 3.5: Andamento del flusso
a vari angoli di incidenza
L'aria che passa sopra l'ala raggiunge il bordo d'uscita prima di quando lo avrebbe raggiunto con l'ala non portante (eccetto quella piccola particella d'aria, invisibile nel disegno, che si è fermata sulla linea di ristagno).L'aria che passa sotto l'ala viene invece ritardata. Questi effetti si estendono a una buona distanza sia sopra che sotto l'ala.
Un'ala (generante portanza ) è meravigliosamente efficace per accelerare l'aria al di sopra di essa. Anche se l'aria che passa sopra l'ala deve compiere un percorso più lungo, arriva dietro prima della corrispondente aria che passa sotto l'ala.
La variazione di velocità è solo temporanea. Come l'aria arriva al bordo d'uscita, ritorna rapidamente alla sua velocità originale (quella della corrente libera), con in più una piccola componente diretta in basso. Anche questo si può vedere nei disegni, in quanto (vedi figura 3.3) la distanza fra due successivi impulsi di fumo torna al suo valore originale
La variazione di posizione relativa è invece permanente.Se si va a vedere l'aria lontano e sottovento all'ala, si vede che l'aria passata sotto l'ala non raggiungerà mai la corrispondente aria passata sopra. Non ci si prova nemmeno.
La figura 3.6 è un grafico che mostra cose si comporta la pressione vicino a un'ala. Tutte le pressioni sono misurate relativamente alla pressione atmosferica nella corrente libera. Le zone in blu, per esempio indicano pressioni negative rispetto all'ambiente, mentre quelle rosse indicano pressioni positive rispetto all'ambiente. Le linee di divisione fra pressione e depressione sono anch'esse indicate nel disegno
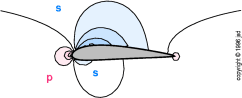
figura 3.6: Pressione
vicino a un'ala
La pressione e la depressione create dall'ala si misurano agevolmente in multipli della pressione dinamica5. Essa è generalmente indicata col simbolo Q. Per una tipica situazione di volo di aviazione generale, Q è circa mezza libbra per pollice quadro( 0.03 atm.). La massima pressione positiva sull'ala è esattamente uguale a Q; questo succede sulla linea di ristagno.6. La depressione massima dipende dall'angolo di incidenza e dalla forma del profilo; per la situazione in figura 3.6 la massima depressione vale circa 0.8 Q. Ogni curva nella figura rappresenta esattamente 0.2 Q (0.1 psi = 0.003 atm)
Studiando questa figura si possono imparare un sacco di cose. Per primo, si vede che il primo quarto circa dell'ala genera metà della portanza. Un'altra cosa da notare è che la depressione sul dorso è assai più importante della pressione sotto l'ala. in figura 3.6, L'ala sta volando con un angolo di attacco di 3 gradi,un ragionevole valore di "crociera" .
In questa situazione, non c'è quasi pressione sotto l'ala; in verità c'è quasi più depressione. La sola ragione per cui l'ala regge il peso dell'aereo è che c'è molto più depressione sul dorso dell'ala. ( C'è una piccola pressione positiva sulla parte posteriore del ventre dell'ala, ma resta il fatto che la depressione sul dorso fa più del 100% dello sforzo necessario a sostenere l'aeroplano.)7
Ancora una volta, questi modelli campi di pressione sono proprio difficili da spiegare in termini di pallottole che rimbalzano sull'ala. Ricordiamoci, l'aria è un fluido e quindi ha una ben definita pressione in ogni punto nello spazio che occupa. Quando questo campo di pressione incontra l'ala, esercita una forza = pressione moltiplicato area.
Ad angoli di attacco più alti, sul ventre dell'ala si generano pressioni positive (più alte di quella atmosferica ), ma sempre meno pronunciate delle depressioni che si sviluppano sul dorso.
La figura 3.7 mostra cosa succede vicino all'ala quando cambiamo l'angolo di attacco: si può vedere che come cambia la velocità, cambia anche la pressione.
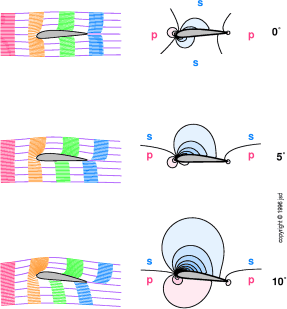
figura 3.7: Flusso e pressione
vicino all'ala
Vien così fuori che che dato il campo di velocità, risulta determinabile il
campo di pressione. Ci sono due modi per calcolarlo; uno lo discutiamo ora,
e l'altro in sezione 3.4.
La pressione da sola non da alcuna forza risultante; è necessaria una differenza di pressione cosicchè un lato della particella venga premuto più dell'altro. Per cui la regola è questa: Dove le linee di flusso sono curve, la pressione ha un gradiente, ossia cambia da punto a punto secondo una determinata direzione
Si può vedere nelle figura che le linee di flusso a curvatura stretta corrispondono ad alti gradienti di pressione e viceversa.
Volendo conoscere la pressione in ogni punto, si può partire da qualche parte e sommare i cambiamenti, punto a punto lungo il percorso che si segue. Questo metodo è matematicamente tedioso (ma tanto chi lavora è un computer..), ma funziona. Funziona persino in situazioni in cui il principio di Bernoulli non è immediatamente applicabile.
Discutiamo ora un secondo modo con cui la pressione è legata alla velocità, detto principio di Bernoulli. nei casi in cui questo principio è applicabile (la maggior parte), questo è di gran lunga il metodo più semplice de elegante.
Il principio di Bernoulli deriva dalla legge di conservazione dell'energia. Esso prende in considerazione l'energia cinetica dell'aria in movimento e l'energia potenziale immagazzinata nell'elasticità dell'aria. Proprio come l'energia può essere immagazzinata in una molla arrotolata, così l'energia viene immagazzinata nell'aria compressa.
La pressione, indicata con Pressure, P, è (per definizione) una forza per unità di area, il che equivale dimensionalmente a energia per unità di volume:9
Evidentemente poi, l'aria in movimento possiede energia cinetica
come ogni massa che si muove
dove v è la velocità locale, e r (la lettera greca "rho" ) è la densità (massa per unità di volume)
Combinando quanto sopra, si conclude:
Adesso facciamo l'ipotesi approssimativa di ignorare altre forme di energia non meccanica (reazioni chimiche, calore prodotto dall'attrito, etc..), e di non aggiungere altra energia all'aria tramite pompe, eliche, o che altro. Allora, basandoci sulla legge che l'energia totale non può cambiare (vedi capitolo 1), concludiamo che l'energia meccanica di una particella d'aria che passa vicino all'ala resta costante.
Ora, se il termine a destra di equation 3.3 è una costante, vuol dire chequando una particella d'aria aumenta la sua velocità, deve diminuire la sua pressione, e viceversa. Questa relazione viene detta Princio di Bernoulli
| Alta velocità vuol dire bassa pressione, e viceversa, |
| per ogni data particella d' aria. |
Talvolta10 succede che tutte le particelle d'aria partano con la stessa energia meccanica. In tal caso si può fare una comparazione, basata sul princio di Bernoulli, fra le diverse particelle d'aria: quelle che si muovono più veloci avranno minor pressione di quelle più lente, avendo la stessa energia meccanica totale.
Il principio di Bernoulli non si può applicare se nel processo hanno un peso importante altre forme di energia che non siano l'enegia cinetica e quella potenziale di pressione. In particolare, nello "strato limite" molto vicino alla superficie di un'ala, l'energia viene costantemente dissipata (trasformata in calore) per attrito. Fortunatamente, lo strato limite è in genere molto sottile (eccetto vicino allo stallo), e se lo ignoriamo del tutto il principio di Bernoulli ci da delle risposte essenzialmente corrette.
Ha senso misurare la velocità locale ( v)in ciascun punto come multipla della velocità della corrente libera ( V) variando una in proporzione all'altra. Similmente ha senso misurare le pressioni relative in termini di pressione dinamica :
che è sempre piccola rispetto alla pressione atmosferica ( assumendo che V sia piccola rispetto alla velocità del suono). La relazione tra pressione e velocità è mostrata graficamente in figura 3.8. La pressione più alta possibile( corrispondente ad aria ferma) vale un Q sopra la atmosferica, mentre l'aria in moto veloce può scendere parecchi Q sotto la pressione atmosferica.
Non ha importanza se si misura P come una pressione assoluta o relativa (relativamente a quella atmosferica). Cambiando da pressione assoluta a relativa si "traslano" di un valore costante i due termini dell'equazione di Bernoulli, e il nuovo valore resta costante ( come in precedenza ) al passaggio della particella d'aria lungo l'ala. Allo stesso modo, se se si usa la pressione relativa in figura 3.8, si può eliminate il termine "Atm" dall'asse della pressione e parlare di "un Q positivo" e di "due Q negativi" -- tenendo presemte che parliamo di pressioni poco sopra o poco sotto una atm.
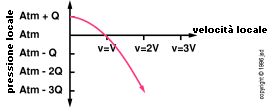
figura3.8: Grafico
Pressione - Velocità
Il Pricipio di Bernoulli ci permette anche di capire perchè esiste una zona di pressione positiva al bordo di entrata dell'ala (che è l'ultimo posto dove ce la si aspetta se si pensa all'aria come a un insieme di proiettili). L'aria alla linea di ristagno è quella che si muove più lentamente di tutto il sistema; è ferma e quindi ha nominalmente la più alta pressione possibile, ossia Atm + Q.
Come già visto nel disegno di sotto di figura 3.7, ad alti angoli di attacco l'ala è estremamente efficace per accelerare l'aria che le passa sopra e ritardare quella che le passa sotto. La massima velocità locale sopra l'ala può essere più del doppio di quella della corrente libera. Questo crea una pressione negativa (depressione) di più di 3 Q.
consideriamo le seguenti linee di ragionamento:
1. L'altimetro dell'aereo funziona misurando la pressione della presa statica. Vedere la sezione 20.2.2 per maggiori dettagli.
2. La presa statica è orientata lateralmente al flusso dell'aria, in un punto scelto in modo tale che la velocità ivi presente sia uguale a quella della corrente libera.
3. In base al Principio di Bernoulli, questa velocità deve essere associata ad una pressione "più bassa " in quel punto.
4.Si può pensare che questa pressione "più bassa" causi grossi errori nell'altimetro in funzione della velocità. In effetti non è così. La domanda è, perchè no?
La risposta ha a che vedere col concetto di "più bassa" pressione. Bisogna chiedersi, più bassa di che? In verità in quel punto la pressione è più bassa di 1 Q risperro all'energia meccanica (per unità di volume) dell'aria. E comunque, nel modello di riferimento, l'energia meccanica dell'aria è 1 Atm + 1 Q. Se da questo valore sottraiamo 1 Q, vediamo che la pressione sulla presa statica è esattamente uguale a quella atmosferica. Quindi l'altimetro da la misura corretta, indipendentemente dalla velocità.
Un altro modo di dire è che l'aria alla presa statica ha 1 Atm di energia potenziale e 1 Q di energia cinetica.
Per contro, l'aria nel tubo di Pitot ha la stessa energia meccanica, 1Atm + 1Q, ma tutta sotto forma di energia potenziale dato che (secondo il nostro modello) non ha energia cinetica.
L'energia meccanica per unità di volume viene ufficialmente chiamata "pressione di ristagno", dato che è la pressione che si osservva nel tubo di Pitot o in ogni altro punto in cui l'aria ristagna, ossia dove la velocità v è zero (rispetto all'aereo).
Nel linguaggio ordinario "statico" e "ristagnante" significano quasi la stessa cosa, ma in aerodinamica indicano due concetti molto differenti. La "pressione statica" è la pressione che si misurerebbe nel sistema di riferimento dell'aria, per esempio a bordo di un pallone che si muovesse galleggiando nella corrente libera. Come aumenta la velocità, la pressione di ristagno sale, ma non quella statica.
Si può anche raffrontare questo con quello che succede in un carburatore.
Qui non cambia il sistema di riferimento, così l'energia meccanica (per unità di volume) rimane 1 Atm. L'alta velocità dell'aria nella gola del tubo Venturi ha una pressione più bassa della pressione atmosferica dell'ambiente.
Per prima cosa, un po'di terminologia:
I non esperti possono non far molta dostinzione fra un fluido "pressurizzato" e un fluido "compresso", ma nella letteratura ingegneristica c'è un sacco di differenza fra i due concetti.
Ogni sostanza sulla terra è compressibile-- sia essa aria, acqua, ghisa o qualsiasi altra. Essa deve aumentare la sua densità quando si applica pressione; altrimenti non ci sarebbe modo di bilanciare le equazioni dell'energia.
Comunque, i cambi di densità non sono molto importanti per capire come lavorano le ali, sino a che la velocità dell'aria non si avvicina (o supera) a quella del suono. Le tipiche velocità dell'Aviazione Generale corrispondono a Mach 0.2 o 0.3 o giù di lì, (anche tenendo in conto gli incrementi locali causati dalle ali), e a queste velocità l'aria non cambia la sua densità che di pochi percento.
Per un gas ideale, la densità è proporzionale alla pressione, per cui può sembrare strano che le variazioni di pressione siano rilevanti e le variazioni di densità no. Ecco il perchè:
In altre parole: Il volo dipende direttamente dalla densità totale ma non direttamente dalla pressione atmosferica totale, solo da differenze di pressione.
Molti libri dicono che l'aria è "incompressibile" in regime subsonico. Questa è una bizzarria che induce in errore. In realtà, quando quei libri usano il termine "flusso incompressibile" generalmente significa che la densità non varia al di là di piccole percentuali. Ciò non ha niente a che fare con il fatto che il fluido abbia un compressibilità alta o bassa. La vera spiegazione sta nel fatto che i cambi di densità sono piccoli perchè i cambi di pressione sono piccoli in rapporto alla pressione atmosferica totale.
Similmente, molti libri dicono che la equazione 3.3 si applica solo a fluidi "incompressibili" . Di nuovo diamo di fronte a un'affermazione che induce a sbagliare. Ecco come stanno in realtà le cose:
Ecco l'equazione di Bernoulli comprendete il termine di secondo ordine. L'ho
riscritta in termini di energia per massa (anzichè energia per volume), per
rendere chiaro che la copressiibilità non interviene, dato che una particella
di massa non cambia (la sua massa) anche se varia il suo volume:
dove r0 è la densità dell'aria alla pressione amosferica,e dove g (gamma) è una costante che compare nell'equazione di stato per il fluido. Il suo valore varia da1.666 per l'elio, 1.4 per l'aria, 1.0 per l'acqua fredda liquida. E' ironico che la correzione è in realtà più piccola per l'aria (che ha alta compressibilità) che per l'acqua (che ha una compressibilità molto inferiore Così non lasciatevi raccontare che il principio di Bernoulli non tien conto della compressibilità. Lo fa, anche nella sua forma più semplice.
Ora siamo al punto che possiamo capire come funzionano gli avvisatori di stallo. Ce ne sono due tipi comunemente utilizzati sui piccoli aerei. Il primo tipo (usato sulla maggior parte dei Piper,Mooneys, e Beechcraft) usa una piccola paletta montata un po' sotto e dietro al bordo d'entrata dell'ala, come mostrato nel disegno di sinistra di figura 3.9. L'avviso viene attivato quando la paletta viene soffiata in alto e in avanti. Ai piccoli angoli di attacco (es. velocità di crociera) la linea di ristagno si trova davanti alla paletta, sicchè questa viene soffiata verso l'indietro e tutti sono felici. Come l'angolo di attacco aumenta, la linea di ristagno si sposta sotto e indietro sotto l'ala. Quando supera la paletta, questa verrà soffiata in avanti e in alto attivando l'avvisatore di stallo
Il secondo tipo di avvisatore di stallo (usato su i Cessna 152, 172, e altri, non incluso il 182) opera su un principo diverso. Esso è sensibile alla pressione sulla superficie anzichè al flusso sulla superficie. Viene posizionato appena sotto il bordo d'entrata dell'ala, come indicato nel disegno di destra di figura 3.9. Ai piccoli angoli di attacco, il bordo d'entrata è una zona di bassa velocità e alta pressione; a grandi angoli di attacco diventa una zona di alta velocità e bassa pressione. Quando la zona di bassa pressione si estende abbastanza sotto il bordo di entrata, verrà risucchiata aria attraverso l'apertura. L'aria, fatta fluire attraverso un'ancia di armonica, produrrà un segnale acustico udibile.
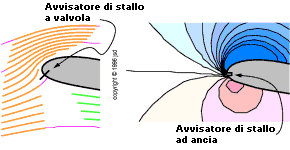
figura 3.9: Avvisatori
di stallo
Si noti che nessuno dei dispositivi rivela realmente lo stallo. Quello che entrabi rilevano in realtà è l'angolo di attacco. Essi servono per dare un segnale qualche grado prima chel'ala raggiunga l'angolo di attacco a cui ci si aspetta lo stallo. Ovviamente se c'è qualcosa che va storto, tipo ghiaccio sulle ali (vedi sezione 3.13), l'ala stallerà a un angolo di attacco più basso di quanto ci si aspetta, e non si avrà nessun avviso dal cosidetto avvisatore di stallo..
Sappiamo tutti che a livello submicroscopico, l'aria è composta di particelle, che sono le molecole di azoto, ossigeno, acqua e di altre varie sostanze. Partendo dalle proprietà di queste molecole e dalle loro interazioni, è possibile calcolare le proprietà macroscopiche come pressione,velocità, viscosità, velocità del suono,etc..
Comunque, per scopi ordinari tipo capire come lavorano le ali, è possibile dimenticare le proprietà di ciascuna particella, visto che le informazioni rilevanti vengono ben evidenziate sulla base delle proprietà macroscopiche del fluido. Questa viene chiamata approssimazione idrodinamica.
Nella realtà, quando si prova a pensare in termini di particelle individuali, è un comune errore sovrastimare la dimensione delle particelle e sottostimare l'importanza delle interazioni fra di esse.
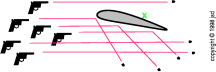
figura 3.10: l'inganno
delle pallottole
Se si immagina, erroneamente, le particelle d'aria grandi e non interattive, più o meno come le pallottole che si vedono in figura3.10, non si capirà mai cone un'ala possa lavorare. Consideriamo i seguenti paragoni. C'è una sola cosa importante che le pallottole e le molecole d'aria hanno in comune:
| Le pallottole colpiscono la faccia inferiore dell'ala, scaricandovi la propria quantità di moto verso l'alto. | Similmente, le molecole d'aria colpiscono il lato inferiore dell'ala, scaricandovi la propria quantità di moto verso l'alto. |
Altrimenti, tutti i punti importanti della storia sono differenti:
| Nessuna pallottola colpisce il dorso dell'ala | La pressione dell'aria sul dorso dell'ala è solo di qualche percento più bassa di quella sul ventre |
| Alle pallottole non importa la forma del dorso dell'ala | Il profilo del dorso è cruciale . uno spoiler posizionato in X in figura 3.10 può facilmente raddoppiare la resistenza dell'intero aeroplano. |
| le pallottole non si colpiscono tra loro, e se lo
fanno ciò no influenza la generazione della portanza
. |
Ogni molecola d'aria colpisce qualche sua vicina 10.000.000.000 di volte al secondo., e ciò è cruciale. |
| Ogni pallottola pesa qualche grammo | Ogni molecola di azoto pesa 0.00000000000000000000005 grammi |
| Le pallottole che passano sopra o sotto l'ala non modificano la loro traiettoria. | L'ala crea un campo di pressione che devia in maniera importante le particelle di fluido, anche se ben lontane |
| Le pallottole non potrbbero spingere in avanti la paletta di un avvisatore di stallo | Il flusso aereo spiega bene come una paletta possa esser spinta in avanti e in alto. vedi sezione 3.5. |
La lista potrebbe ancora andare avanti, ma quanto sopra dovrebbe bastare a render l'idea. Le interazioni fra le molecole d'aria costituiscono la parte grossa del discorso. E' una approssimazione migliore pensare all'aria come a un fluido continuo piuttosto che come a un fascio di proiettili
Può darsi di sentire discorsi che cercano di spiegare come un'ala genera portanza utilizzando l'effetto Coanda o l'effetto cucchiaio.Questi discorsi sono completamente errati, come discusso in sezione18.4.4 e in sezione 18.4.3.
Ci sono dozzine di altri errori sull'argomento, ma va oltre lo scopo di questo libro discuterli o anche solo catalogarli.
Quasi tutti avremo sentito dire che un'ala genera portanza perchè è curva sul dorso e piatta sotto. Ma non si sono mai visti i piloti da manifestazione volare a testa in giù per considerevoli periodi di tempo? Non viene il sospetto che ci dev'essere qualcosa di sbagliato nella storia del dorso curvo e ventre piatto ?
Ecco una lista di cose necessarie in un aeroplano inteso per il volo rovesciato:
Da notare che il cambio della sezione alare non è nella lista. Come mostrato in figura 3.11, un'ala ordinaria vola anche invertita. Può sembrare un po' strano volare con la superficie piana spopra e quella curva sotto, ma si può fare.

figura 3.11: Volo rovesciato
L'errore comune per cui si pensa che l'ala debba essere curva sopra e piatta sotto deriva dalla già discussa errata convinzione che l'aria debba passare al di sopra e al di sotto dell'ala nello stesso tempo. In realtà, un'ala rovesciata genera portanza esattamete per lo stesso princiop di un'ala dritta

figura 3.13:
Terminologia dei provili
Per aiutarci a discutere la forma dei profili, figura3.12 illustra un po' di terminologia utile.
Un profilo simmetrico, con le superfici inferire e superiore immagini speculari una dell'altra, ha camber =0 .Gli andamenti del flusso e della pressione per un tale profilo sono mostrati in figura 3.13.

figura 3.13: Profilo simmetrico
Questa figura può essere considerata come vista laterale di un'ala simmetrica, o vista dall'alto di un timone di direzione.Anche i timoni sono profili alari, e lavorano sugli stessi principi.
A piccoli angoli di attacco, un profilo simmetrico lavora meglio del corrispondente profilo curvo. Per contro, ad angoli di attacco più alti, un profilo curvo lavora meglio del corrispondente simmetrico. Un esempio di ciò si vede in figura 3.14. Il profilo designato"63-1-012'' è simmetrico, mentre quello designato ``63-1-412'' è curvo; per il resto sono identici.11 Ad gni normale angolo di attacco (sino a circa 12 gradi), i due profili generano una portanza virtualmente uguale. A partire di lì il profilo curvo ha iun grosso vantaggio perchè non stalla sino ad un agolo di attacco assai più alto. Come conseguenza, il suo coefficiente di portanza massimo è più grande.
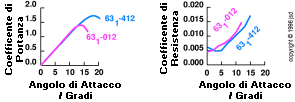
figura 3.14:
la curvatura previene lo stallo
A grandi angoli di attacco, il bordo d'entrata di un'ala curvata taglierà il vento con un angolo minore rispetto al corrispondente di un'ala simmetrica. Questo non prova niente, ma da una spiegazione intuitiva del perchè le ali curve hanno una maggior resistenza allo stallo.
L'ammontare della curvatura in un tipico profilo moderno è solo l'1 o 2 per cento-- ovviamente non categorico. Una ragione per cui le ali non sono più curvate è che un ulteriore aumento di curvatura richiederebbe poi la faccia inferiore concava-- cosa difficile e laboriosa da realizzare. Un'altra ragione sta nel fatto che una granda curvatura da benefici solo in prossimità dello stallo (es. decollo e atterraggio) e per creare una curvatura supplementare in questi casi è sufficiente estendere i flap quando necessario.
La curvatura negativa è chiaramante una cattiva idea (anticipa lo stallo), così gli aerei che vogliono buone prestazioni in volo rovesciato(es. Pitts o Decathlon) hanno profili simmetrici (camber = 0).
Abbiamo visto che in condizioni ordinarie la portanza generata da un'ala dipende dall'angolo di attacco, ma a ben poco dalla curvatura. Ciò ha un senso. In effetti un aereo sarebbe non pilotabile se la portanza fosse determinata solo dalla forma dell'ala. Dato che la curvatura non può essere cambiata durante il volo, non ci sarebbe modo di cambiare il coefficiente di portanza. L'aereo potrebbe portare il suo peso solo ad una ben precisa velocità e sarebbe instabile e incontrollabile. In realtà il pilota (e il trim) regola in continuazione la portanza regolando l'angolo di attacco, parametro ben più importante; vedi capitolo 2 e capitolo 6.
L'ala usata dall'aereo dei fratelli Wright è sottile, molto curvata e piuttosto concava nella superficie inferiore. La si può vedere in figura 3.15. Non c'è differenza significativa fra le due superfici (sopra e sotto). stessa lunghezza, stessa curvatura. Comunque, l'ala genera portanza utilizzando gli stessi principi di ogni profilo. Questo dovrebbe ulteriormente dissipare la convinzione che l'ala porta per la differenza di lunghezza delle due superfici inferiore e superiore.
Simili ossrvazioni si applicano alla vela di una barca. Questa è un'ala molto sottile, orientata più o meno in verticale, che produce una portanza laterale.

figura 3.15: Il profilo
Wrights 1903
Persino un oggetto piatto e sottile. tipo una qualunque tavola piana produce portanza, se il vento lo investe con un appropriato angolo di attacco.Il modello di flusso (idealizzato) per una tavola ( o di un'ala piatta di un modellino di aliante di balsa) lo si vede in figura 3.16. Ancora una volta, il meccanismo che genera la portanza è lo stesso.

figura 3.16:tavola piatta
Si può essere stupiti del fatto che i diagrammi del flusso in figura3.16 o nelle precedenti figura siano i soli permessi dalle leggi dell'idrodinamica. La risposta è quasi, ma non del tutto. figura 3.17 mostra la tavola piatta che lavora con lo stesso angolo di attacco (e la stessa velocità) di figura 3.16, ma il diagramma del flusso è diverso.

figura 3.17: tavola piatta
-- linee di flusso innaturali

figura 3.18: tavola piatta
--circolazione pura
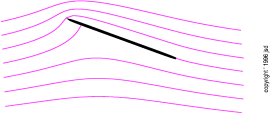
figura 3.19: tavola piatta--linee
di flusso naturali
Il diagramma di flusso (figura 3.17) è perfettamente simmetrico. Ho eliminato le informazioni temporali, per chiarire che le linee di flusso non cambiano capovolgendo l'immagine destra-sinistra o sopra-sotto. La linea di ristagno anteriore è a una certa distanza dietro il bordo d'entrata; la linea di ristagno posteriore è alla stessa distanza davanti al bordo d'uscita. Questo modello di flusso non produce alcuna portanza. (Ci sarà un grosso momento -- il cosidetto momento di Rayleigh-- ma non portanza.)
La differenza fra queste figura è la circolazione --la figura 3.16 ha la circolazione, mentre la figura 3.17 no. (Figura 3.19 è la stessa figura 3.16 senza informazioni temporali.)
Per capire la circolazione e i suoi effetti, cominciamo con immaginare un aeroplano con le ali fatte a tavola piatta, parcheggiato sulla rampa in una giornata senza vento. Immaginiamo quindi di muovere con un ventaglio l'aria, creando un flusso circolatorio attorno all'ala, nel senso muso-coda sopra l'ala e viceversa sotto ( senso orario nella figura).Questo è il modello di flusso di circolazione pura, che si vede in figura3.18. Supponiamo che poi inizi a soffiare un vento di prua (da sinistra a destra in figura). In ogni punto dello spazio, i due campi di velocità si sommeranno. Il flusso circolatorio e il vento si sommeranno sopra l'ala, producendovi alta velocità e bassa pressione. Il flusso circolatorio cancellerà parzialmente il vento sotto l'ala, producendovi bassa velovità e alta pressione.
Se prendiamo il fusso non circolatorio(sinistra-destra) in figura 3.17 e sommiamo ad essso vari valori di circolazione, potremo generare tutti i campi di flusso in accordo con le leggi dell'idrodinamica, incluso il reale flusso naturale che si vede in figura 3.16 e figura 3.19.12
Non c'è niente di speciale circa le tavole piatte; i profili reali hanno analoghi campi di flusso, come si vede in figura 3.20, figura 3.21, e figura 3.22.
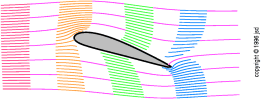
figura 3.20:
flusso innaturale - c'è angolo di attacco ma non circolazione
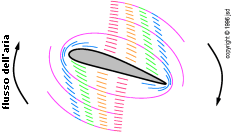
figura 3.21: circolazione
pura

figura 3.22: normale flusso
naturale
Se si accelera improvvisamente un'ala, partendo da ferma, il campo di flusso iniziale sarà non-circolatorio, come in figura 3.20. Fortunatamente per noi, l'aria odia senza rimedio questi campi di flusso, e giusto il tempo di percorrere una breve distanza (circa due lunghezze di corda o giù di li) sviluppa abbastanza circolazione per chè si abbia il normale campo di flusso di figura 3.22.
nelle situazioni reali di volo, si verra a stabilire esattamente la circolazione necessaria a far si che la linea di ristagno posteriore venga a coincidere con uil bordo d'uscita, così che l'aria non debba ruotare attorno ad esso. Ovviamente, la circolazione che annulla il flusso attorno al bordo d'uscita, più o meno duplicherà il flusso sul bordo d'entrata.
La regola generale.-- detta conditizione di Kutta -- cioè che l'aria detesta girare l'angolo su un bordo di uscita affilato. In prima approssimazione, l'aria detesta girare ogni bordo affilato, in quanto l'alta velocità in quel punto causa un sacco di attrito. Riguardo alle ali ordinarie, che ci interessa conoscere, il bordo d'uscita è l'unico affilato.
La cosa strana è che se il bordo di uscita è affilato, il profilo lavora persino se è affilato anche il bordo di entrata . Questo spiega il perchè deil funzionamento degli aliantini di balsa, anche se hanno un bordo d'entrata affilato.
E' un po' misterioso il perchè l'aria detesti girare l'angolo al bordo di uscita e poi non si ponga il problema di girare un bordo d'entrata affilato, -- ma così è. 13 Ciò è in relazione al ben noto fatto che soffiare è cosa ben diversa dall'aspirare.( Basti pensare che si riesce a spegnere una candela, soffiando, anche da mezzo metro,, ma aspirando con pari forza da più di qualche centimetro neanche si muove la fiamma). In ogni caso la rego la è:
| L'aria vuole lasciare in modo pulito il bordo di uscita |
Come aumernta l'angolo di attacco, aumenta la circolazione necessaria a soddisfare la condizione di Kutta.
Ecco un bel modo diretto per dimostrare la condizione di Kutta.A un'altiudine di sicurezza, partiamo con l'aereo 14 in cofigurazione pulita e in volo livellato, con una velocità superiore di un paio di nodi a quella in cui inizia a suonare l'avvisatore di stallo. Mantenendo l'assetto longitudinale costante e il volo livellato, estendiamo i flaps . L'avvisatore di stallo si metterà a suonare. Non c'è bisogno di stallare l'aereo, l'avvisatore stessso fa il punto .
Questa dimostrazione evidenzia come i flaps ( che sono dietro all'ala) abbiano un grande effetto sul flusso attorno all'intera ala, compreso l'avvisatore di stallo ( che sta sul davanti)
L'estensione dei flaps ( mantenendo l'assetto longitudinale e la direzione di volo costanti ) aumenta l'angolo di attacco. Questo aumente la circolazione, che attiva l'avvisatore di stallo come descritto in sezione 3.5.
Ecco un risultato bello e semplice: la portanza è uuguale alla velocità, moltiplicato la circolazione, moltiplicato la densità dell'aria, moltiplicato l'apertura alare. Questo è detto teorema di Kutta.-Zukowsky.
| Portanza = velocità × circolazione × densità × apertura alare |
Dato poi che la circolazione è proporzionale al coefficiente di portanza e alla velocità, questa nuova nozione è in accordo con quella precedentemente nota che dichiara la portanza proporzionale al coefficiente di portanza per il quadrato della velocità.
E' possibile visualizzare la circolazione guardando il campo di velocità. In figura 3.23, la linea nera veticale mostra dove si troverebbe la "timeline" dei 70 millisecondi se non ci fosse l'ala. lLa " timeline" de1 70 millisecondi reale è data dal bordo destro dei filetti blu.

figura 3.23: la
circolazione fa accelerare gli indicatori di flusso superiori e ritarda quelli
inferiori
A causa del contributo della circolazione alla velocità, gli indicatori di flusso sopra l'ala vengono accelerati (relativamente alla velocità del flusso libero), mentre quelli al di sotto vengono rallentati.
Guardando indietro la figura 3.7, si vede che la circolazione è proporzionale all'angolo di attacco. In particolare si nota che quando un profilo non genera portanza, non vi è circolazione -- gli indicatori di flusso superiori non sono accelerati rispetto a quelli inferiori.
La stessa cosa si vede confrontando le figura 3.20 e figura 3.22 --
La circolazione si può misurare con la seguente procedura. Stabiliamo un anello immaginario attorno all'ala, e percorriamolo in senso orario dividendolo in un gran numero di piccoli segmenti. Pe ogni segmento, moltiplichiamo la lunghezza del segmento stesso per lacomponente della velocità dell'aria lungo la direzione dell'anello in quel punto (Se la velovità è opposta a quella dell'anello, il prodotto sarà negativo.) Sommiamo tutti i prodotti., e il totale sarà la misura della circolazione. Questa la definizione ufficiale.
Cosa interessante, il risultato è indipendente dalla forma e dalla lunghezza dell'anello.15 Per esempio,se si va molto lontano, la velocità sarà più bassa, ma il percorso più lungo, sicchè il prodotto lungezza -velocità resta immutato.
C'è una diffusa convinzione (errata ) che sia la velocità relativa alla superficie dell'ala a generare la portanza. Ciò causa infinite confusioni.
Ricordiamo che l'aria ha una ben definita pressione e velocità in ogni punto, non solo sulla superficie dell'ala. Si può andare in ogni punto vicino o lontano dall'ala con un anemometro e un manometro e misurare velocità e pressione. Il flusso circolatorio stabilito dall'ala crea baassa pressione in una vasta zona estendentesi soprra l'ala. La velocità in ogni punto ivi determina la pressione..
La circolazione vicino a un'ala è in genere causata dall'interazione deol vento con la forma del l'ala. Ma ci sono altri modi per stabilire il flusso circolatorio. In figura 3.24, le ali non hanno la classica forma del profilo, ma sono fatte come mulinelli a palette. Facendo ruotare questi mulinelli potremo generare un campo di flusso circolatorio con la forza bruta.
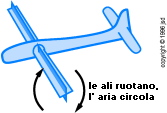
figura 3.24: aereo con ali
a mulinello
Il pricipio di Bernoulli si applica punto per punto nell'aria vicino all'ala, creanando una bassa pressione al di sopra di essa che spingerà l'ala in alto, anche se l'aria vicino all'ala non ha alcuna velocità relativamente ad essa, dato che si suppone sia imprigionata tra le palette. Anche qui vale il teorema di Kutta-Zukovsky, come già enunciato: la portanza è uguale a velocità per circolazione per densità dell'aria per apertura alare..
Questo fenomeno--la creazione della circolazione necessaria alla portanza facendo girare l'aria meccanicamente-- viene detto effetto Magnus.
L'aereo di figura 3.24 avrà problemi di controllabilità, visto che l'angolo di attacco non esiste (vedi capitolo 2 e capitolo 6). Il concetto, comunque, non è così ridicolo come può sembrare a prima vista. Il famoso studioso di aerodinamica Flettner costruì un'imbarcazione che attraversò a vela l'Atlantico, usando come "vele" grossi cilindri rotanti nel vento
E' anche più facile ancora la verifica di questo importante concetto. Non c'è bisogno di mulinelli a quattro o più palette, basta una superficie piana., un biglietto da visita va benissimo. Lasciamolo cadere da un metro e mezzo circa, col suo asse maggiore orizzontale . Al momento di lasciarlo, proviamo ad imprimergli un po' di rotazione attorno al suo asse maggiore. Volerà sorprendentemente bene; il rapporto portanza -resistenza non sarà enorme, ma neanche zero. Il movimento è illustrato in figura 3.25.
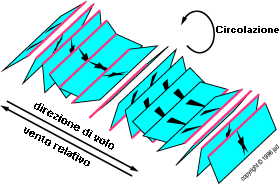
figura 3.25: Cartoncino
volante --portanza generata dalla circolazione
Si possono migliorare le prestazioni dando all'ala un miglior allungamento (più apertura-meno corda).Una volta presi un raccoglitore e tagliai delle striscie lunge 11 pollici e larghe un pollice; funzionavano egregiamente.
Come esperimento, provate a dare la direzione della circolazione nel senso sbagliato (p. es. con la parte sopra che va controvento). cosa pensate succederà?
Vi invito caldamente a provare da soli questi esperimenti. Migliorerà la vostra comprensione intuitiva sul nesso tra portanza e circolazione.

figura 3.26: Palle curve
Possiamo usare queste idee per capire qualcosa (ma non tutto ) sull'aerodinamica delle palle da tennis e cose simili .come raffigurato in figura 3.26, se una palla viene colpita in modo da imprimerle molta rotazione all'indietro (backspin), la superficie della palla ruotante su se stessa creerà il campo di circolazione necessario per generare portanza, e sarà una palla "galleggiante". Per contro, uno "smash" implica rotazione della palla in avanti (topspin) che produce una portanza negativa, che fa si che la palla "voli" verso terra più veloce di quanto farebbe sotto l'influenza della sola gravità. Simili discorsi valgono per le palle deviate lateralmente.
Per avvicinarci di più alla risposta giusta, ci dobbiamo chiedere dove il vento relativo è lento o veloce, relativamente al centro della palla, non alla superficie in rotazione. Teniamo presente che un fluido ha una pressione e una velocità in ogni suo punto, non solo sulla superficie della palla. L'aria che scorre sopra uina superficie crea resistenza, non portanza. Bernoulli dice che quando una particella d'aria accelera o decelera, trasforma la sua energia cinetica (velocità) in energia potenziale (pressione). Per la palla galleggiante ("floater" ) il flusso circolatorio causato dalla sua rotazione all'indietro si combina con il flusso libero creato dal movimento in avanti della palla, per creare una zona di alta velocità e bassa pressione sopra la palla, che è appunto la portanza.
Questa semplice immagine di circolazione meccanicamente indotta si applica meglio alle palle che hanno una ruvidità uniforme sula loro superficie. Le palle da cricket stanno in una categoria differente, dato che hanno una cucitura sporgente sul loro "equatore". Se ad esse si imprime una rotazione che stabilizzi l'orientamento della cucitura, e si fa"volare" la cucitura con un determinato angolo di attacco, il flusso sopra la cucitura causa una extra -turbolenza che favorisce il flusso laminare su un lato della palla. Si veda sezione 18.3 per un confronto fra flusso laminare e turbolento. Questi effetti sovrastano la circolazione indotta meccanicamente.
Per capire veramente palle e cilindri volanti, occorrerebbe tener conto dell'effetto diretto della rotazione sulla circolazione, dell'effetto della rotazione sulla separazione, dell'effetto della cucitura sulla separazione, etc... Questo va oltre lo scopo di questo libro .
Il funzioanamento di un'ala è molto più facile da comprendere
Un vortice consiste in una certa quantità d'aria che circola attorno a se stessa. L'asse attorno a cui ruota l'aria viene detto linea di vortice. E'matematicamente impossibile per una linea di votice avere estremità libere. Un anello di fumo è un esempio di vortice. La sua linea di vortice si chiude su se stessa per cui non ha estremità libere.
La circolazione necessaria a produrre la portanza può essere attribuita a una linea di bound vortex (vortice avvolgente l'ala). Essa è legata all'ala e viaggia con l'aeroplano. Sorge la domanda, cosa succede a questa linea di vortice alle estremità dell'ala?
La risposta è che il vortice fuoriesce da ogni estremità dell'ala . Ogni ala forma un trailing vortex (vortice di estremità) (detto anche wake vortex - vortice di scia) cha si estende per miglia dietro l'aereo. Questi vortici di scia costituiscono la continuazione del bound vortex. Vedi figura 3.27. Assai lontano dietro l'aereoplano, magari all'inizio di tutto il percorso che ha fatto l'aereo da quando ha lasciato l'effetto suolo, i due vortici di estremità (trailing vortex) si ricongiungono formando una linea di vortice ininterrotta.
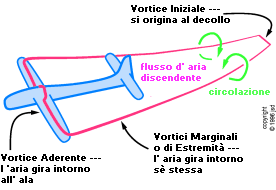
figura 3.27: Vortici
avvolgenti (bound), vortici di scia (trailing)
L'aria ruota attorno alla linea di vortice nel senso indicato in figura. Sappiamo che l'aereo per sorreggere il suo peso, deve spingere in giù sull'aria. L'aria che è stata "visitata" dall'aereoplano avrà perciò un moto in discesa rispetto al resto dell'aria. I vortici di estremità segnano il confine di quest'aria discendente.
Non ha importanza considerare la vorticità come causa o come effetto dell'aria discendente -- non si può avere l'una senza l'altra.
La portanza deve eguagliare il peso moltiplicato il fattore di carico, e non si può facilmente cambiare peso, densità dell'aria,o apertura alare. Quindi, quando l'aereo vola a basse velocità, deve generare più circolazione.
E' una comune convinzione (sbagliata) che i vortici di estremità siano un qualcosa associato a flusso diperso inutilmente,e che possano essere eliminati utlizzando fences, winglets, et cetera. La verità è che i vortici sono assolutamente necessari; non si può generare portanza senza generare vortici. Giocando con la forma dell'ala, i progettisti possono controllare da dove i vortici si staccano, ma non c'è modo sbarazzarsi dei vortici senza sbarazzarsi della portanza.
Le winglets incoraggiano i vortici a lasciare l'ala al''estremità e non in qualche altro punto dell'apertura alare. Questo produce più portanza, perchè solo la parte di ala che porta circolazione genera portanza, in accordo col teorema di Kutta Zukovsky. Ancora, come regola generale, l'aggiunta di un paio di winglets di un metro l'una non produce vantaggi aerodinamici rispetto ad allungare le ali orizzontalmente di un metro per lato.16
Il " bound vortex" (vortice avvolgente) che produce la circolazione che sostiene il peso dell'aereo non va confuso con i piccoli vortici prodotti dai generatori di vortici ( per ridare energia allo strato limite) come discusso in sezione 18.3.
Quando il controllo del traffco (ATC) dice "attenzione .. turbolenza di scia'' in realtà dice che qualche aereo precedente ha lasciato un vortice di scia sul nostro percorso. I vortici di scia di un aereoplano grosso e pesante possono facilmente far incappellare uno piccolo e leggero.
Un aereo pesante, tipo un C5-A in volo lento rappresenta il pericolo maggiore, in quanto necessita di moltissima circolazione per sorreggere tutto il suo peso a bassa velocità. Si potrebbe pensare che un C5 -A con i flasp estesi sia poi la cosa peggiore in assoluto, ma non è esattamente vero. I flaps incrementano la capacità delle ali di creare circolazione, ma non si estendono per tutta l'ala.. Per cui una parte della circolazione lascia l'ala dove finiscono i flaps, e il resto alle estremità . Se si vola nella scia di un altro aereo, due vortici di media forza causano meno dolori di uno solo di grande forza. Quindi ci si deve aspettare che i pericoli derivanti dai vortici di scia siano massimi quando si vola dietro un aereo pesante, lento e in configurazione pulita.
Come un anello di fumo, i vortici di scia non stanno fermi, si muovono. In questo caso verso il basso. Una regola grossolana dice che scendono di circa 2-3 metri al secondo, ma questo dipende dall'apertura alare e dal coefficiente di portanza dell'aereo che li ha prodotti.
I vortici fanno parte dell'aria, e se c'è vento, i vortici vengono trasportati nella sua sirezione. In realà, la ragione per cui i vortici discendono, sta nel fatto che il vortice destro viene portato in basso dal campo fi flusso che stabilisce quello sinistro, e viceversa. Sovrapposto a questo campo flusso, il vento porta via i vortici in maniera ovvia.
Quando una linea di vortice arriva vicino a terra, "vede la sua riflessione". Ciò significa che si muove come se ci fosse una linea di vortice speculare ad essa al di sotto del livello del terreno; questo fa si che i vortici si "allarghino": il vortice destro comincia a spostarsi a destra, e il sinistro a sinistra.
Se si vola su un aereo leggero, si deve evitare la zona dietro e sotto a un aereo grande. Evitare questo spazio per un minuto o due in genere è sufficiente, in quanto i vortici più vecchi di così in genere hanno perso abbastanza intesità per non costituire più un problema serio.
Se si sta atterrando sulla stessa pista su cui è atterrato un grosso aereo, si può evitare la turbolenza di scia con un avvicinamento alto e ripido, atterrando in un punto ben avanti rispetto a dove esso è atterrato. Ricordiamo che non avrà generato vortici quando non avrà più generato portanza. Supponendo poi di atterrare controvento, il vento non farà altro che aiutarci a tenerci liberi dai vortici
Decollando dalla stessa pista dove è decollato un aereo grande, si possono evitare i vortici -- in teoria -- staccandosi dalla pista ben prima di dove lo ha fatto laereo grosso e se si è sicuri che la nostra rampa di salita sta ben sopra e/o dietro la sua. In pratica questo può essere difficile da fare, dato che l'altro aereo può essere capace di salire più ripidamente di noi. Inoltre, visto che probabilmente si decolla controvento, occorre stare in guardia che il vento può spostare i vortici dell'altro aereo verso di noi.
Un leggero vento al traverso può mantenere un vortice sulla pista più a lungo, opponendosi all'allontanamento laterale. Un problema più raro è che il vento latale può trasportare sulla nostra pista i vortici da una pista parallela
La tecnica che richiede meno sofismi resta comunque quella di attendere qualche minuto prima di decollare, in modo che i vortici si disperdano e si indeboliscano dissipando in attrito la loroo energia.
Ecco alcuni ulteriori vantaggi dierivanti dall'aver ben capito circolazione e vortici: ci si spiega la resistenza indotta, e ci si spiega perchè gli alianti hanno ali strette e lunghe. La resistenza indotta e comunemente detto sia il "prezzo" della generazione della portanza. Ma non esiste nessuna legge fisica che richieda un prezzo definito. Se si potesse prendere una gran quantità d'aria, e spingerla dolcemente verso in basso, si potrebbe sostenere il proprio peso a un costo molto basso. Il prezzo che assolutamente bisogna pagare è quello dovuto per la generazione dei vortici di estremità.
Per ogni km. che l'aereo percorre, ogni estremità alare fa un km di vortice. Il movimento circolatorio in questi vortici implica quantità non trascurabili di energia cinetica: --energia--, ed è per questo che si ha la resistenza indotta. Un'ala lunga e stretta necessiterà di meno circolazione di un'ala corta e larga che produca la stessa portanza. . Gli alianti (che hanno bisogno di volare lentamente con minima resistenza) devono quindi aver ali lunghe e sottili (unico limite: la robustezza-- è difficile fare qualcosa che sia lungo, sottile e robusto).
Ora possiamo comprendere come funzionano le procedure di decollo da campi soffici. Quando l'aereo è in effetto suolo, "vede la sua riflessione" sul suolo. Se si vola a tre metri da terra, l'effetto è lo stesso di avere un aereo-immagine speculare che vola tre metri sotto terra. I vortici di estremità di questo aereo girano in senso opposto ed annullano in gran parte i nostri vortici di estremità, riducendo abbondantemente la resistenza indotta.
Come già visto in sezione 13.4, in un decollo da campo soffice, occorre staccarsi da terra a velocità molto bassa ,e quindi volare per un po' in effetto suolo. Non ci sarà attrito (o danni) alle ruote, dato che non toccano il tirreno. Ci sarà una piccola resistenza indotta, perchè in effetto suolo, e ci sarà poca resitenza parassita dato che la velocità è bassa. L'aereoplanao accelererà come un pazzo. Raggiunta la normale velocità di volo, si alza il muso e si vola via.
Le norme( Federal Aviation Regulations ) proibiscono il decollo quando vi è ghiaccio aderente alle ali o alle superfici di controllo, a meno che non venga "pulito a liscio".
E' interessante il fatto che non richiedono che sia interamente rimosso, ma solo "pulito a liscio".
Ci sono ragioni aerodinamiche molto buone per questo.

figura 3.28: La rugosità
degrada le prestazioni dell'ala
Nella sezione 3.4, si è visto che il principio di Bernoulli non può dare risultati corretti quando viene tolta energia dal sistema per attrito. Il ghiaccio, urtando nel vento, è molto efficace nel togliere energia al sistema. questo tende a de-energizzare lo strato limite, dando inizio alla separazione che produce lo stallo.17
E' intesessante il fatto che ad angoli di attacco piccoli o moderati ( velocità intorno a quella di crociera) il ghiaccio non ha quasi nessun effetto sul coefficiente di portanza. Ciò riconferma quanto già detto in sezione 3.11, ossia che non è la velocità relativa alla superficie che genera la portanza.
Talvolta la temperatura dell'aria è appena sopra quella di congelamento, ma a causa di precendenti situazioni o del calore ceduto per irraggiamento l'aereo è più freddo e coperto di ghiaccio. In questi casi un secchio di acqua calda funziona egregiamente.
Abbiamo visto che nella generazione della portanza sono implicati vari principi fisici. Ognuna delle seguenti affermazioni è corretta comunque.
Esaminiamo ora le relazioni fra questi principi fisici. Sarà mica che abbiamo una parte della portanza per Benoulli e un'alto po' per le leggi di Newton ? No, le leggi fisiche non sono cumulative in questo senso.
Nella realtà c'è un solo processo che genera la portanza. Ognuna delle affermazioni precedenti si concentra su un differente aspetto di questo processo. L'ala produce circolazione proporzionalmente al suo angolo di attacco (e alla sua velocità). Questa circolazione fa si che l'aria sopra l'ala si muova più velocemente.Questo a sua volta produce bassa pressione in accordo col princio di Bernoulli. La bassa pressione tira in alto l'ala e spinge in basso l'aria in accordo con le leggi di Newton.
Per un aereo in volo stabile e livellato, le forze in gioco si bilanciano tra loro. Sappiamo dalla terza legge di Newton. 18 che per ogni forza ce ne deve essere un'altra uguale ed opposta da qualche parte, ma ecco l'idea speciale che ci debba essere una forza uguale ed opposta localmente per mantenere l'equilibrio.
La terra tira giù l'aereoplano( per gravità). Questa forza è bilanciata localmente perchè l'aria spinge in su l'aereo (a causa del campo di pressione vicino alle ali) . Naturalmente la stessa pressione che spinge in su l'aereo spinge in giu l'aria; e questa forza viene trasmessa da una particella d'aria all'altra giu sino alla superficie della terra. Alla superficie, la pressione spinge in giu la terra e in su l'aria. La forza diretta verso il basso sulla terra è giusto l'occorrente per bilanciare il fatto che l'aereo attira verso l'alto la terra (per gravità)
Dato che la forza è la quantità di moto per unità di tempo, lo stesso processo può essere descritto comeun grande circuito chiuso di flusso di quantità di mot. oLa terra trsferisce quantità di moto verso il basso all'aereo (per gravità). L'aereoplano trasferisce quantità di moto vero il basso all'aria( per il campo di pressione in prossimità delle ali). Questa quantità di moto viene poi trasferita, particella per particella di aria, verso il basso siono alla terra (tramite la pressione sulla superficie), completando il ciclo.
Per capire bene come stanno le cose occorre guardare la figura 3.27. Se si osservano le cose come in figura3.2, non si riuscirà mai a comprendere come funziona il bilancio delle quantità di moto, perchè questa figura non mostra la situazione in maniera completa. Può venir la tentazione di fare i seguenti ragionamenti sbagliati:
Per risolvere questo paradosso, teniamo presente che figura 3.2 non dice tutta la storia. Essa mostra solo gli effetti del "bound vortex" (vortice che avvolge l'ala) che corre lungo l'ala, ma non mostra gli effetti del vortice di estremità. Così ciò che si vede vale solo relativamente vicino all'ala e lontano dalle estremità.
Guardiamo la figura e scegliamo un altro punto, ad esempio mezza lungezza di corda davanti all'ala. Si vedrà che in quel punto l'aria ha una certa quantità di moto diretta verso l'alto. Tutti i punti sopra e sotto quel punto, con il campo di velocità rappresentato nella figura, hanno anch'essi una quantità di moto diretta verso l'alto. Ma vien fuori che se si sale o si scende da quel punto più di un'apertura alare o giù di li, si trova che tutta l'aria ha una quanrità di moto diretta verso il basso. Questo è causato dai vortici di esremità, che inducono un flusso verso il basso. Vicino all'ala domina il vortice avvolgente, ma se si va più in alto o più in basso sono i vortici di estremità ad essere dominanti.
In realtà, se si sommano tutte le quantità di moto di una colonna d'aria, per tutte le colonne davanti all'ala si trova che la quantità di moto verticale è zero. L'effeto totale del vortice di estremità annulla esattamente l'effetto del vortice avvolgente.
Se si considerano i punti direttamente davanti all'ala (non sopra o sotto) si ha un annullamento in parte differente.. L'effetto del vortice d'estremità non è mai abbatanza per invertire il flusso, per cui c'è sempre un certo flusso diretto verso l'alto davanti all'ala, non importa quanto lontano davanti. Ma l'effetto del vortice di estemità ne riduce di molto l'entità, sicchè il flusso diretto verso l'alto diventa presto trascurabile. Questo è il motivo per cui si può parlare di aria "indisturbata" davanti all'aereo.
Dietro l'ala non c'è invece alcun genere di annullamento; il flusso verso il basso dell'ala viene solo rinforzato dal flusso verso il basso del vortice di estremità. C'è una grande quantità di moto verso il basso dietro l'ala.
La regola generale è semplice: C'è quantità di moto diretta in basso in ogni colonna d'aria che passa attraverso l'anello di vortice (che si vede in figura 3.27). Non c'è quantità di moto in ogni colonna d'aria che stia daventi all'ala, esternamente ai vortici di estremità, o dietro il vortice di partenza.
Così ora possiamo comprendere il bilancio della quantità di moto: mano a mano che l'aereoplano vola, continua a imprimere sempre più quantità di moto verso il basso all'aria, aumentando la dimensione della zona dietro di se dove l'aria si muove verso il basso.
[Precedente] [Sommario] [Successivo]
[Commenti o domande]
Copyright © 1996-2001 jsd