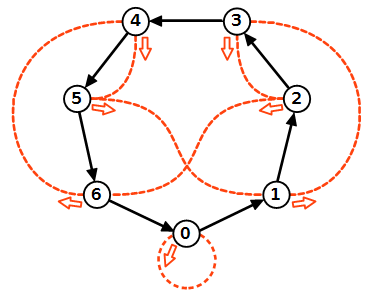
Una passeggiata in questo grafo vi permetterà di sapere il resto della divisione di qualunque numero naturale per 7 senza eseguire la divisione e usando soltanto le cifre del numero stesso.

fig

Ecco come si usa.

Considerate per esempio il numero 654.

---

1) 654 è formato dalle cifre 6, 5, 4.

2) Partite dal nodo 0 del grafo.

3) Seguite 6 frecce nere in successione e poi una freccia arancione (arrivate sul 4).

4) Proseguite con 5 frecce nere e una freccia arancione. (arrivate sul 6)

5) Proseguite con 4 frecce nere (arrivate sul 3).

6) Il numero del grafo su cui siete arrivati a fine percorso è il resto della divisione: 654 : 7 = 93 con resto 3.

7) Se finite sullo 0 allora il numero di partenza è divisibile per 7.

---

Ma... come e perché funziona?

18 APRILE 2015 - DAL FORUM

Segnalazioni dal Forum di BASE Cinque

Cari amici, aprile dolce dormire, dice il proverbio. E BASE Cinque dorme già dal 14 marzo.

Però il Forum è sempre sveglio e attivo, per cui invito tutti a parteciparvi!

Dalla filiera inaugurata da Ivana Niccolai riporto tre interessanti segnalazioni:

Bruno Berselli segnala il libro: Bruno D'Amore, Arte e matematica, Edizioni Dedalo, 2015.
Pietro Vitelli segnala l'interessante blog di Cristina Sperlari, maestra di scuola primaria: Il piccolo Friedrich.
Adam Atkinson annuncia la 6° edizione della conferenza MathsJam, che si terrà il 7 e l'8 novembre 2015. Per farvi un'idea potete consultare gli archivi delle edizioni precedenti.

14 marzo 2015 - SCIENZA

Bicchieri rotolanti

Articolo pubblicato sul blog invitoallanatura.it

fig

Con due bicchieri di plastica fabbrichiamo un rullo convesso.

Con altri due bicchieri fabbrichiamo un rullo concavo.

Facciamo rotolare i due rulli su un binario di legno in discesa e osserviamo cosa succede.

Potremo imparare qualcosa sul meccanismo di retroazione e sull'equiibrio di un sistema dinamico con una spruzzatina di geometria qua e là.

4 febbraio 2015 - ALBUM - ANALISI

ALBUM (2) - La forma di una goccia d'acqua

Inverno 2015. Una stalattite di ghiaccio si sta fondendo.

Gocce d'acqua cadono a intervalli regolari.

Mi avvicino con la macchinetta fotografica e cerco di coglierne qualcuna.

Esiste una una fomula matematica per esprimere la forma delle gocce d'acqua?

E quella delle stalattiti di ghiaccio?

fig

7 gennaio 2015 - ALBUM - GEOMETRIA - TOPOLOGIA

ALBUM (1) - Il teorema della curva di Jordan

Cari amici, ci sono molti argomenti matematici interessanti che non riuscirò mai ad approfondire su BASE Cinque ma che desidero segnalarvi per i notevoli spunti didattici che possono offrire.

Perciò ho deciso di metterli nell'ALBUM.

Quello che vedete in figura è un poligono di 2006 lati.

Dato un qualunque punto che non si trovi su un lato (per esempio il punto nero), come si fa a stabilire se esso è interno o esterno al poligono?

smileyjordan

Credit: Robert Bosch

E' questo un esempio molto semplice di arte matematica chiamata TSP Art (Traveling Salesman Problem Art). Il professor Robert Bosch ci spiega qui come costruire questo genere di figure.

A me è stata utile per presentare il teorema della curva di Jordan.

Una meravigliosa proposta didattica su questo argomento si trova nel libro:

Franco Ghione, Tau topologo, La fiaba che racconta la matematica superiore ai bambini, illustrata da 16 pitture originali di Mario Schifano, Editrice La Città del sole, 1985.

Suggerisco in particolare il capitolo intitolato Il gioco dell'isola (PDF).

Per approfondire, un buon punto di partenza è la tesi di laurea:

Federica Sebastianelli, Teorema della curva di Jordan (PDF), tesi di laurea discussa all'università Alma Mater Studiorum, Bologna, a.a. 2010-2011.

Pace e bene a tutti!

Gianfranco Bo

Data creazione: dicembre 2015

Ultimo aggiornamento: dicembre 2015

xhtml 1.1

Sito Web realizzato da Gianfranco Bo