Buon capodanno a tutti con la Coppa
Deregowski![BASE Cinque - Appunti di Matematica ricreativa]
Buon capodanno a tutti con la Coppa
Deregowski!
Qui sopra
dovrebbe vedersi un video AVI.
Osservate la base della coppa.
Prima
che finisca il 2010, aggiungo alla Biblioteca il libro di Ian Stewart,
La piccola bottega delle curiosità matematiche del professor Stewart,
Codice edizioni, Torino, 2010.
Cito dalla prefazione dell'autore: "La matematica che avete visto a scuola non è tutto. Meglio ancora: nella matematica che avete visto a scuola ci sono cose interessanti. Anzi, ce ne sono un bel po’, soprattutto quando non dovete preoccuparvi di un compito in classe o di far tornare i conti."
Un piccolo esempio topologico. Può essere utile a capodanno!
Chi è capace
di liberare l'anello di corda
senza togliere la mano dalla tasca,
né tagliare la corda,
né infilare la corda in tasca e farla passare sotto le dita?
Clicca qui per la risposta, ma
prima pensaci!
Attenzione: Giò Rapa mi segnala i disegni di Ian
Stewart sono poco chiari,
perciò mi sono permesso di correggerli.
Niente di nuovo sotto il Sole, ma il libro può essere utile a scuola. Purtroppo, il prezzo è la nota dolente: più di 50000 Lire (26 Euro) per 300 pagine in brossura mi sembra decisamente troppo. Si può trovare in Italia la versione originale inglese a meno di metà prezzo (12,60 Euro). Su Amazon, la versione in paperback costa 11,53$ mentre la versione digitale costa 13,56$.
Un solido curioso
(ideato da Jan Deregowski).
I tranelli della visione a tre dimensioni: a seconda di come lo guardi, questo poliedro convesso può sembrare un cubo, un prisma triangolare o una specie di tronco di piramide, ma non è nessuno dei tre.
Cari amici di Base Cinque, auguro a tutti voi buon Natale e un felice 2011!
Colgo l'occasione per regalarvi un mio piccolo contributo a una famosa illusione ottica basata sulle post-immagini (after-images)
Fissate per circa 20 secondi la crocetta bianca che si trova al centro della figura qui sopra. I vostri occhi devono essere sempre immobili e puntati sulla crocetta.
Spostate poi gli occhi sulla parete di fronte a voi e sbattete le palpebre.
Che cosa vedete?
Ma... come si realizzano queste figure?
Ti presento il decimetro cubo
(più o meno)
Il decimetro cubo è un cubo che ha lo spigolo lungo 1 dm, ovvero 10 cm. Ma che cosa succede se la misura non è esattamente quella giusta?
I due cubi sovrapposti che vedete nella foto qui sotto hanno misure leggermente diverse: il lato del cubo grande è 10 cm, mentre il lato dell'altro cubo è 8 cm. La differenza è soltanto il 20% del lato più grande.
Tuttavia, se parliamo di volumi, il cubo più piccolo è circa la metà di quello più grande!
Dalle dissezioni geometriche al
Teorema di Pitagora
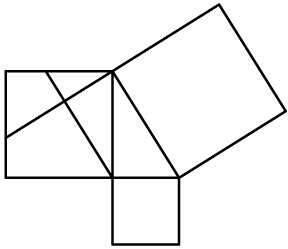
In Geometria, la dissezione è la divisione di un poligono in parti che ricomposte formino un altro poligono equivalente al primo. Le dissezioni sono utili, per esempio, per dimostrare le formule delle aree.
Esiste una dissezione semplice da realizzare e facile da ricordare che dimostra il Teorema di Pitagora?
Aggiornata la Biblioteca di Base Cinque
con un nuovo libro:
Robert Ghattas, Bricologica. 32 oggetti matematici da costruire con le mani, Sironi, 2010.
Ogni oggetto di Bricologica dimostra qualche interessante proprietà geometrica o numerica. Ci sono grandi classici come il Tangram, il caleidoscopio e gli origami. Ci sono oggetti matematici interpretati per divertire: come il nastro di Moebius che si trasforma in un gioco a vento, o i solidi platonici con i vertici di formaggio, da servire come stuzzichini a una festa. E, ancora: oggetti quotidiani visti nel loro aspetto matematico, come il calendario a cubi, le trecce o le stelle di carta.
Il T-puzzle e le sue
sorprese (aggiornamento)
Il quadrato magico "SATOR"
(aggiornamento)
Ringrazio il Dr. Rino John Gliosca che mi ha inviato questa fotografia del Quadrato Magico che si trova nella chiesa di Santa Maria Ester. La località esatta è Acquaviva Collecroce, in provincia di Campobasso.
Il test della Domenica del
Corriere
Chi si ricorda... 
...?
Nel 1952, ogni settimana, nella rubrica Giochi e passatempi, c'erano sempre due o tre problemi matematici. Purtroppo erano quasi tutti banalissimi. Ne ho scelto cinque, tra i più interessanti, per dare l'idea di come si "giocava" con la matematica circa 60 anni fa.
Cari
amici di BASE Cinque, leggo attentamente tutte le e-mail che ricevo.
Purtroppo, per motivi di tempo, non riesco rispondere a tutte. Vi prego di
scusarmi, ma ho preso la dolorosa decisione di archiviare le e-mail
precedenti al 1 settembre 2010 alle quali non ho risposto. Spero così (ma non
garantisco) di mettermi in pari e di mantenere il passo, in futuro.
Come si può utilizzare a scuola il materiale che si trova su BASE Cinque?
I problemi raccolti nell'Archivio
di questo sito sono organizzati per aree disciplinari
(aritmetica, geometria, topologia, combinatoria, etc) e non per livello di
istruzione. Questo perché i problemi più belli della matematica ricreativa si
possono affrontare a vari livelli di approfondimento, dalla scuola elementare
alla scuola superiore e oltre.
Perciò il consiglio che dò è il seguente: cercate nel sito i problemi adeguati
alla vostra programmazione e che possono diventare sfide per i vostri alunni.
Con il copia & incolla trasferiteli nel vostro word
processor preferito e rielaborateli adattandoli alle vostre esigenze
didattiche.
Come esempio, inserisco due test che ho proposto in una classe seconda media
per far riflettere i ragazzi su alcuni aspetti importanti del fare matematica:
l'accurata lettura del testo, l'acutezza di ingegno, l'attenzione a tutti i
particolari e la capacità di uscire dagli schemi.
Il test di Bertoldino 2010 (PDF)
Il test del primo gradino (PDF)
Nota: si può fare il copia & incolla di testo e immagini anche dai file PDF.
Aggiornata la Biblioteca con il doppio DVD-Rom
contenente tutti gli articoli pubblicati sui primi 500 numeri della rivista
Le Scienze. Sono anche presenti le 350 rubriche di giochi
matematici curate, andando a ritroso nel tempo, dai Rudi
Matematici, Ian Stewart, Alexander
Dewdney, Douglas Hofstadter e, dulcis in fundo,
Martin Gardner, il principe dei Giochi Matematici. Si trova in
edicola.
Ho
inserito in via sperimentale nel colonnino a destra il
servizio Google News Bar. Troverete ogni giorno nuove
notizie sulla matematica, i matematici e i giochi matematici.
Perché alcuni puzzle geometrici bi- e tri-dimensionali sono
straordinariamente utili nell'insegnamento della matematica?
Perché fanno capire che una presupposizione ingiustificata può ostacolare la
risoluzione di un problema fino a renderla impossibile (o errata). Inoltre,
tale preconcetto a volte è difficile da scovare perché si mimetizza molto
bene.
Un bell'esempio è dato da questa piramide a 5 pezzi. Il compito è il seguente:
costruire una piramide a base quadrata usando i 5 pezzi che vedete nella
fotografia qui sotto.
Avete per caso già presupposto qualcosa?
Va bene, ma dove si trova questo gioco? Io l'ho trovato in una bancarella al mercatino della notte bianca di Bra (Cuneo), ma ho visto che viene proposto anche nel sito Logica Giochi (http://www.logicagiochi.com/). L'acquisto si può fare sia online, sia presso negozi elencati nel sito stesso.
Nikolai
Bogdanov-Belski, Alla porta della Scuola, 1887.
20 settembre 2010
A tutti i colleghi
insegnanti,
agli studenti e ai
genitori
auguro
Buon anno
scolastico!
Ma...
come va la scuola in Italia?
"Quest'anno la scuola mette al centro gli studenti e non gli interessi corporativi. È fondamentale il diritto dei ragazzi ad avere una scuola di qualità indipendentemente dal loro ceto sociale e dalla regione di appartenenza."
"La sfida deve essere raccolta innanzitutto dagli insegnanti perchè a loro tocca l'onere di applicarla e di collaborare per rendere la scuola davvero un'istituzione eccellente. Occorre restituire a questa realtà che credo sia uno degli elementi unificanti del paese la giusta considerazione e il giusto valore. Oggi la sfida è degli insegnanti."
(dall'intervista a Mariastella Gelmini, ministro dell'Istruzione, Università e Ricerca scientifica, pubblicata sul Corriere della sera.it il 13 settembre 2010)
Aggiornata la Biblioteca con due nuovi
libri:
Pietro Gorini, Enigmi matematici, L'Airone, Roma, 2010.
Giovanni Filocamo, Il matematico curioso, Kowalski, Milano, 2010.
Aggiornata la Biblioteca con un nuovo
libro:
Eric Temple Bell, I grandi matematici, RIZZOLI BUR Alta Fedeltà, Milano 2010.
Finalmente, dopo 13 anni, una nuova edizione in italiano del mitico libro Man of Mathematics del 1937. Perché questo libro è mitico? Prima di tutto perché è una miniera di informazioni e aneddoti sulla vita di 31 grandi matematici da Zenone a Cantor, poi perché presenta le loro idee in modo molto semplice e infine perché il capitolo dedicato a Pierre de Fermat convinse Andrew Wiles a impegnarsi nella dimostrazione del famoso Ultimo Teorema di Fermat.
Ecco una dichiarazione tratta dall'intervista a Wiles pubblicata sul sito del Progetto Polymath (Politecnico di Torino).
“E’ vero. Il libro di Bell [Man of Mathematics] lo lessi quando avevo dieci anni. Presentava il Teorema di Fermat in modo così semplice che anch’io, pur essendo ancora un bambino, riuscivo a capirlo e mi resi conto che, da quel momento, non l’avrei mai più dimenticato. La sua risoluzione divenne il mio primo impegno.”
Andrew Wiles ci mise 13 anni, dal 1985 al 1998, ma alla fine ci riuscì!
Relax on a
rainbow, di Ellis Nadler (su toonpool)
Albert Einstein e la quarta
dimensione
Un vecchio indovinello geometrico riproposto sotto forma di aneddoto nel libro di Maria Toffetti, Campo estivo per giovani geni, A. Mondadori, 2009.
In sintesi, l'indovinello è questo.
Nella figura qui sotto, vedete 4 triangoli equilateri costruiti con 12 stecchini uguali. Ok?
Eliminiamo un triangolo, ovvero 3 stecchini. Con i rimanenti 9 stecchini, siete capaci di costruire di nuovo 4 triangoli equilateri uguali a quelli della figura?
Fatto? Bravissimi!
Ora eliminiamo un altro triangolo. Con i rimanenti 6 stecchini, siete capaci di costruire ancora 4 triangoli equilateri uguali a quelli della figura?
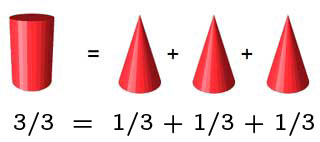
Come calcolare il volume della sfera senza versare neanche una goccia d'acqua sulla tovaglia.
La cifra più sorprendente di
pi-greco
Un bicchiere, un boccale da birra, una bottiglia di aceto.
In quale di questi casi l'altezza del recipiente è maggiore della sua circonferenza?
Aggiornata la Biblioteca di carta con tre
nuovi libri:
Albrecht Beutelspacher, Le meraviglie della matematica. Sessantasei esperienze spiegate attraverso i numeri, Adriano Salani Editore (Ponte Alle Grazie), 2008. Ristampato nel 2010 tra i saggi della rivista Focus.
Benoit Rittaud, Viaggio nel paese dei numeri, Edizioni Dedalo, 2008.
Benoit Rittaud, I misteri del caso, Edizioni Dedalo, 2009.
Il test di Gerry
(Scotti). Una scelta di quiz matematici presentati a "Chi vuol
essere milionario?"
Aggiornata la pagina I quesiti più
famosi con un nuovo problema e relativa soluzione inviati da
Giovanni Antonio Chirilli.
Il problema delle 8 monete
Siano date otto monete di cui una falsa e di peso inferiore alle altre. Utilizzando non piu' di due pesate con una bilancia a bracci uguali, si determini qual è la moneta falsa.
Questo problema è particolarmente istruttivo perché la sua soluzione è unica.
Il quadrato magico "SATOR"
(aggiornamento)
A Perugia, nell'Hotel Fortuna, si trova un affresco moderno nel quale è citato il quadrato magico SATOR. Ecco due particolari dell'affresco.
8 marzo
2010. Con un tremendo ritardo, nella Giornata Internazionale della
Donna, faccio i miei migliori auguri a tutte le donne del mondo e in
particolare alle donne matematiche di tutti i tempi.
In questa occasione desidero presentarvi Danica Mae McKellar (nata nel 1975) che, se non vi distrarrete troppo..., potrebbe aiutarvi ad amare la matematica.
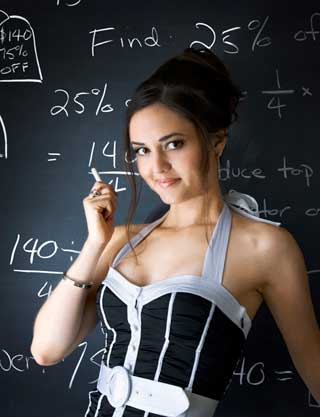
Se siete incuriositi, scoprite chi è usando un motore di ricerca.
... 
E' nato
prima l'uovo o la gallina? Aggiornato Le
galline e la matematica con un simpatico contributo di
Infinito.
Aggiunta alla Biblioteca di BASE Cinque la Open Library (Biblioteca aperta), dove si
possono trovare online e scaricare molti classici della matematica, fra cui
A synopsis of elementary results in pure and applied mathematics, di
George Shoobridge Carr, London, 1880, uno dei testi più amati
dal grande matematico indiano Srinivasa Aiyangar Ramanujan.
Il calendario a due
dadi. Alla Fiera di S. Antonio, per un euro, ho comprato questo
calendario. I nomi dei 12 mesi sono scritti su 3 parallelepipedi di legno. Le
cifre dei numeri dei giorni sono scritte sulle facce di due dadi cubici.
Ruotando opportunamente i dadi, si possono mostrare tutte le date da 01 a
31.
Il problema è: come si devono disporre le cifre sulle facce dei due dadi per poter mostrare tutti i numeri da 01 a 31?
L'ultimo uomo,
un altro micro-racconto fantascientifico di Roberto Magari.
Rifugio antiatomico,
un racconto di Roberto Magari.
Ho scaricato questo racconto e altri scritti del grande matematico Roberto Magari dal sito http://www.dsmi.unisi.it/web/magari/, nel 2005.
Oggi quel sito non si trova più in rete, perciò ho pensato di riproporre su BASE Cinque questo bellissimo racconto che mi è rimasto sempre impresso nella mente.
Qui
sotto vedete il ritratto del matematico tedesco Hermann
Grassman (1809-1877).
Eppure, in Internet si sta diffondendo la leggenda che esso sia il ritratto di Christian Goldbach (1690-1764).
Per esempio, qui (http://www.matematika.it/matematici.php), qui (http://www.gruppoeratostene.com/storia/storia.htm) e qui (http://goldbach.pl/goldbach_weak_conjecture_info_pl.php).
Per trovarne altri, basta cercare Christian Goldbach su Google-Immagini o su Bing-Immagini.
xhtml 1.1
Sito Web realizzato da Gianfranco Bo