[BASE Cinque - Appunti di Matematica ricreativa]
Il diario di BASE Cinque - 2023
20 dicembre 2023
[A23-61] Augurio
Cari amici, mi aiutate a completare le caselle vuote scrivendo qualche proprietà unica e speciale dei numeri indicati?
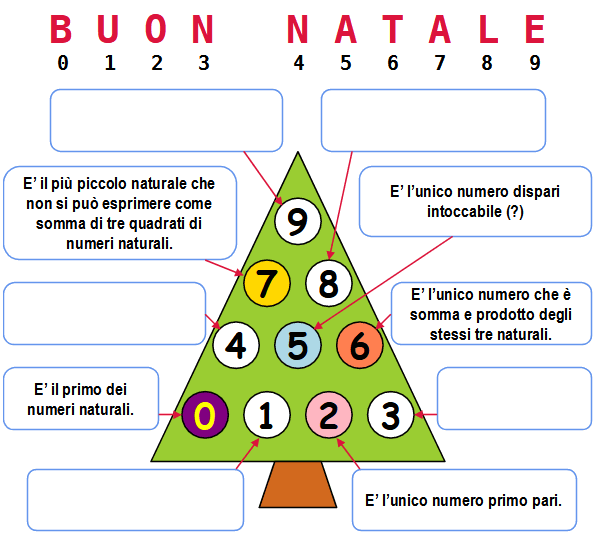
Nota. Un numero intoccabile è un numero che non è la somma dei divisori propri di nessun altro numero.
I divisori propri di un numero sono i suoi divisori positivi escluso il numero stesso. Per esempio, i divisori propri:
di 6 sono 1, 2, 3;
di 8 sono 1, 2, 4.
I numeri primi hanno un solo divisore proprio che è 1.
16 dicembre 2023
[A23-60] Scrivere tutte le cifre di π
Cari amici, come certamente sapete, π è un numero irrazionale. La sua scrittura decimale ha infinite cifre e non diventa mai periodica.
Quindi è IMPOSSIBILE scrivere TUTTE le le cifre di π su un foglio limitato.
Oppure è invece possibile?
E quanto potrebbe essere grande questo foglio?
Chi potrebbe scriverlo?
Quanto tempo impiegherebbe?

Per rispondere bisogna attivare la fantasia matematica e supporre di:
- usare una penna senza massa con un pennino geometrico che tracci linee senza spessore con un inchiostro senza atomi;
- scrivere su un foglio geometrico, come il piano euclideo;
- scrivere a una velocità arbitrariamente alta caratteri arbitrariamente piccoli.
14 dicembre 2023
[A23-59] Brick e kite
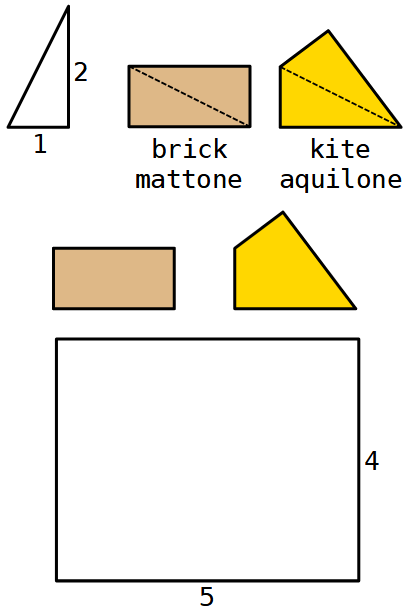
Con 2 triangoli rettangoli di cateti lunghi 1 e 2 si costruiscono due tipi diversi di piastrelle chiamati brick e kite, come mostrato nella figura.
Si chiede di piastrellare un rettangolo di dimensioni 5×4 usando entrambi i tipi di piastrelle.
Quanti bricks e quanti kites servono?
Nota.
Dalle esplorazioni di Livio Zucca e George Sicherman.
Grazie a Franco dal Forum!
11 dicembre 2023
[A23-58] Dov'è l'errore?
La figura mostra il classico cerchio unitario nel piano di Gauss.
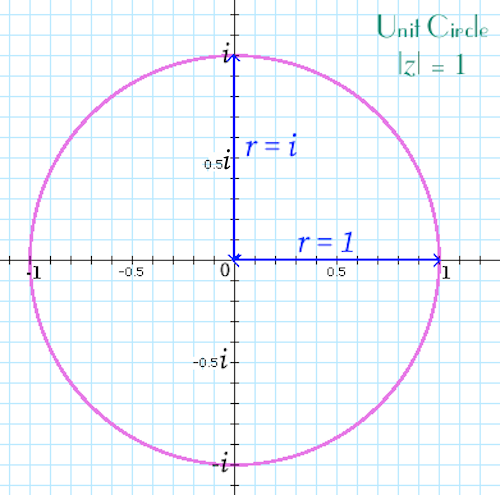
Se uso il suo raggio 1 allora l'area del cerchio è π.
Se invece uso il suo raggio i allora l'area del cerchio è -π.
Dov'è l'errore?
---
Risposta immediata: la lunghezza del raggio è il modulo del vettore che rappresenta il numero complesso e vale sempre 1, perciò l'area del cerchio vale π.
| 1 + 0i | = | 0 + i | = 1
Grazie a Paolo e Quelo dal Forum!
Ma potrebbe esistere un mondo immaginario dove le lunghezze fossero
immaginarie?
Mah...
8 dicembre 2023
[A23-57] Eugenio Raffo xilografo
Dal 2 dicembre 2023 al 7 gennaio 2023 si può visitare la mostra “Eugenio
Mario Raffo: il poeta del legno” nella sala espositiva al secondo
piano del Palazzo Fascie Rossi a Sestri Levante.
Un'esposizione bella,
interessante, ricca di spunti didattici con la possibilità di "toccare" le
matrici e di osservarle riflesse in uno specchio. Complimenti alle
organizzatrici e agli organizzatori.
Scattando qualche fotografia alle matrici di legno inciso, si possono fare esperimenti interessanti di grafica al computer. Il più semplice consiste nel creare l'immagine simmetrica rispetto a un asse verticale, come illustrato figura seguente.
Eh sì, se vuoi fare un disegno da stampare come un timbro devi disegnarlo al contrario destra/sinistra.

5 dicembre 2023
[A23-56] Suggerimento di secondo livello
Questo fumetto trovato in rete è il seguito di una vecchia barzelletta.
Il ragazzo alla lavagna, in un episodio precedente, aveva sbagliato interpretando un punto esclamativo come se fosse un fattoriale.
Questa volta non vuole ripetere l'errore perciò interpreta l'ultimo punto esclamativo proprio come punto esclamativo.
Purtroppo questa volta i due punti esclamativi indicano un fattoriale doppio... e sbaglia di nuovo.
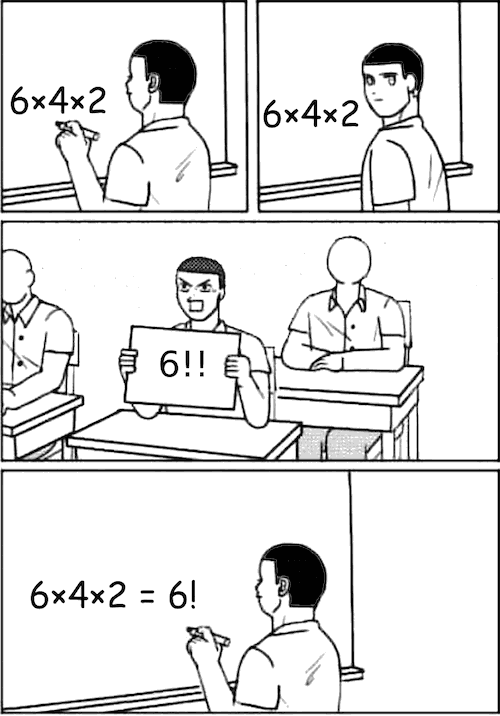
Aggiornata la pagina Il lato comico.
30 novembre 2023
[A23-55] Sette cose che mi piacciono di D. R. Kaprekar

- Dattatreya Ramachandra Kaprekar (1905-1986) è stato un matematico indiano in gran parte autodidatta.
- Trascorreva ore felici risolvendo enigmi matematici.
- Si guadagnava da vivere insegnando Matematica nella middle school di Devlali.
- Stampava e diffondeva privatamente i propri articoli sotto forma di opuscoli con iscrizioni come Published by the author, Devlali, India.
- Molti matematici indiani ridevano delle sue invenzioni aritmetiche, ritenendole banali e poco importanti.
- Molti altri matematici erano incuriositi dalle sue invenzioni, per esempio i Devlali numbers, meglio conosciuti come self numbers.
- I self numbers sono i numeri interi positivi che NON
si possono ottenere come somma di un numero m e delle sue
cifre, per qualsiasi m.
La loro sequenza si trova si OEIS (A003052).
Domandina 1) Quale dei numeri 29, 30, 31 è un self number e perché? Domandina 2) Come tradurre in italiano "self number", "digitaddition", "digitaddition generator"?
23 novembre 2023
[A23-54] Il linguaggio di wxMaxima
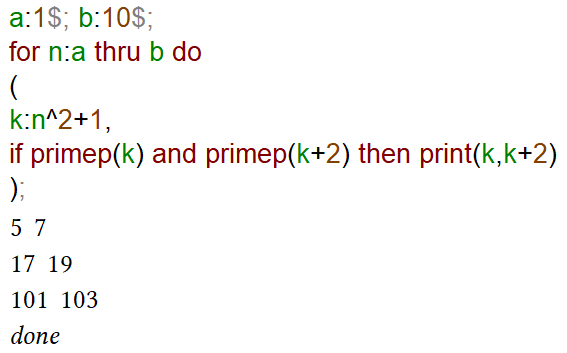
Ecco un programmino che trova e stampa tutti i numeri primi del tipo n2+1 che hanno un primo gemello nell'intervallo [a,b].
E' scritto nel linguaggio di wxMaxima.
---
---
Mi piace usare linguaggi di programmazione interpretati, piuttosto che compilati perché così si instaura una specie di dialogo con il computer.
Oggi si usa la parola coding invece di programmazione, ma forse non sono esattamente sinonimi.
16 novembre 2023
[A23-53] Primi gemelli ricorsivi
Aggiornata la pagina Il lato comico.
L'umanità è pronta per costruire il quarto piano significativo di questa torre?
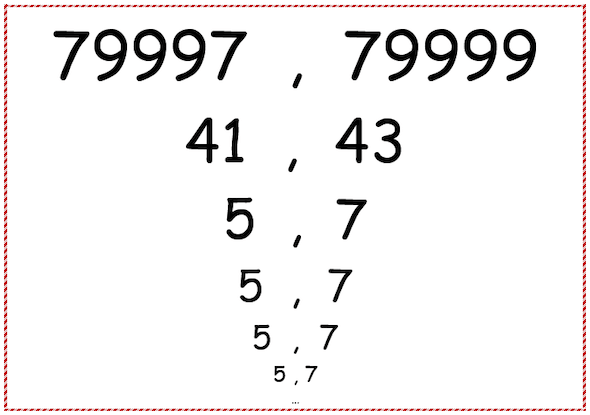
79997 e 79999 sono due primi gemelli le cui somme delle cifre
sono due primi gemelli le cui somme delle cifre
sono due primi gemelli le cui somme delle cifre
sono due primi gemelli le cui somme delle cifre
sono due primi gemelli le cui somme delle cifre
…
9 novembre 2023
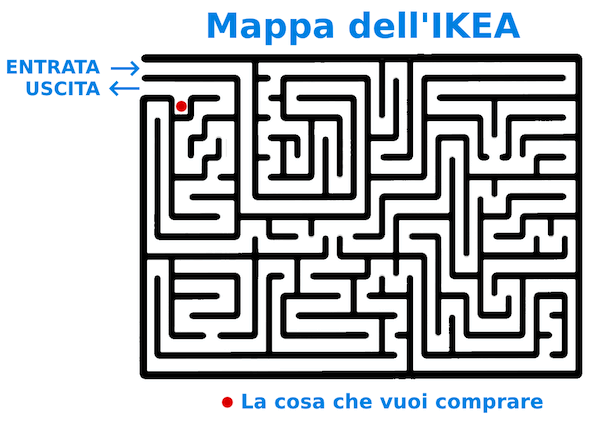
[A23-52] Mi serviva un KÅKKIØL
Ce l'hanno solo in un noto negozio svedese.
Provate a raggiungere mentalmente il pallino rosso. Ho abbattuto due muri per facilitarvi l'impresa.
P.S. Il KÅKKIØL è una CAZZUOLA da muratore svedese.
Aggiornata la pagina Il lato comico.
2 novembre 2023
[A23-51] Matematica col punto esclamativo
Aggiornata la pagina Il lato comico.

---
Gli zeri di dieci
Ci sono 2 zeri alla fine del numero 10!
---
26 ottobre 2023
[A23-50] Rete minima nel cubo (2)
Ecco alcuni risultati dal Forum.
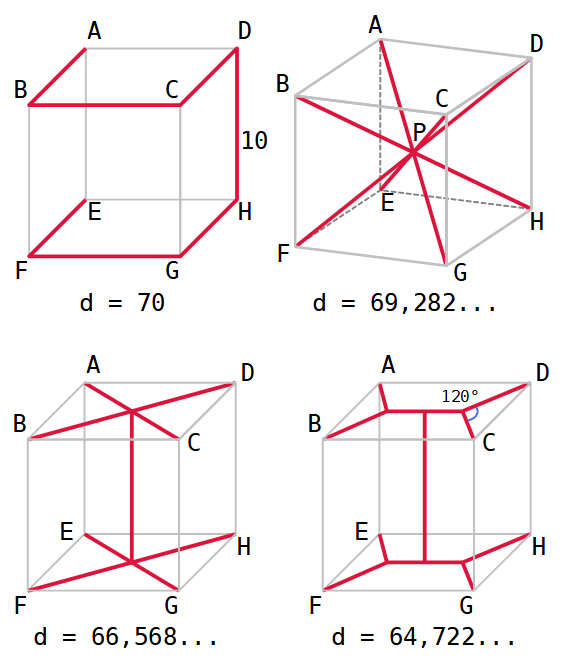
Chi sa migliorare ancora questa rete?
Grazie Maurizio e Franco.
https://www.base5forum.it/viewtopic.php?f=1&t=8747&p=29565#p29565
19 ottobre 2023
[A23-49] Rete minima nel cubo (1)
Questo problema è un'estensione in 3 dimensioni di un classico problema della rete stradale ottima tra i vertici di un quadrato.
---
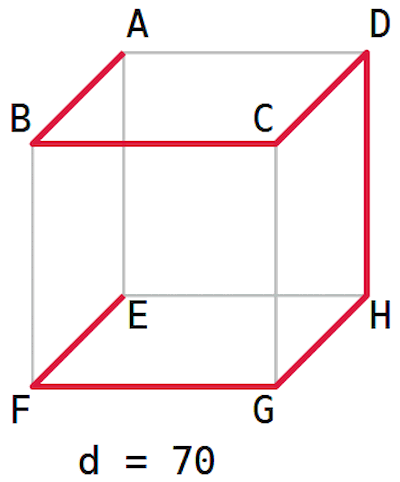
Abbiamo 8 punti che si trovano sui vertici di un cubo di lato 10.
Vogliamo costruire una rete di condutture rettilinee che permettano di andare da qualunque vertice a qualunque altro vertice.
Vogliamo che la lunghezza totale di tutte le condutture sia la più piccola possibile.
La figura mostra un esempio di rete, ma non quella più più corta.
Come è fatta la rete più corta e quanto misura?
16 ottobre 2023
[A23-48] Ancora collegamenti
Cari amici, OK, questo è un classico, tanto per tenersi in allenamento.
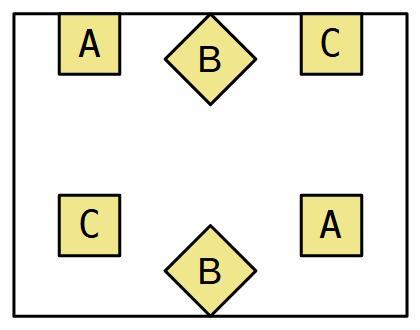
Disegnate tre linee che colleghino i quadrati gialli, rispettivamente A con
A, B con B e C con C.
Però ci sono dei divieti da rispettare:
1) Le linee non devono incrociarsi fra loro.
2) Le linee non devono attraversare i quadrati gialli e neppure sfiorarli.
3) Le linee non devono uscire dal rettangolo grande che delimita la figura.
9 ottobre 2023
[A23-47] Un gioco quasi hamiltoniano
La tavola del gioco Starburst, che si vede nella foto, è un grafo a 8 vertici.
Lo scopo del gioco è di segnare 7 vertici, uno dopo l'altro, tali che abbiano un cammino hamiltoniano.
Mi chiedo: il grafo a 8 vertici usato nel gioco Starburst è quasi-hamiltoniano, nel senso che ogni suo sottoinsieme di 7 vertici ha un cammino hamiltoniano?
E' possibile disegnare il grafo in un altro modo per facilitare il gioco?

---
Il puzzle è stato segnalato da Jeremy Kun su Mastodon e da David Eppstein sul suo blog 11011110.
2 ottobre 2023
[A23-46] Matematica con i nonni
Oggi, 2 ottobre, è la festa dei nonni che in terra e in cielo sono i nostri angeli custodi. Volevo mettere assieme nonni e matematica e mi sono venute in mente alcune immagini che avevo visto anni fa in un libro.

Queste immagini mi piacciono anche perché mostrano che i nonni hanno la forza di portare i nipoti sulle spalle per aiutarli a vedere più lontano.
Dei nonni ti puoi fidare anche quando ti tengono a testa in giù per farti capire i vettori antiparalleli.
E fanno tutto questo sorridendo, anche se hanno mal di schiena.
Le figure sono tratte dal libro:
Walter Warwick Sawyer, Vision in Elementary Mathematics, 1964.
Sulla copertina c'è il carattere cinese che significa "felicità".
Auguri e felicità a tutti i nonni!
---
Il libro è stato digitalizzato da Internet Archive nel 2023.
Nel libro, l'adulto è un papà ma oggi mi piace pensare che sia un nonno.
1 ottobre 2023
[A23-45] Togli triangoli (2)
Questa griglia di 32 triangoli equilateri di lato unitario ha il perimetro uguale a 16.
Si possono togliere due triangoli in modo da far aumentare il perimetro.
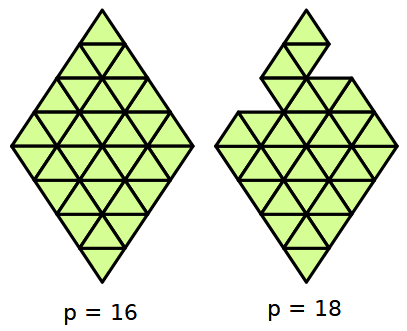
1) Continua a togliere triangoli, uno alla volta in modo da far aumentare al massimo il perimetro della figura. Quanti triangoli hai tolto?
2) Quante forme diverse di perimetro massimo si possono ottenere?
Precisazione. La forma ottenuta deve essere un poligono semplice: niente buchi, niente intrecci.
29 settembre 2023
[A23-44] Togli un altro quadrato
Quanti quadrati al massimo puoi togliere da una griglia senza far cambiare la misura del suo perimetro?
---
La famiglia di problemi che vi propongo in questo articolo ha a che fare con un concetto importante di geometria piana: l'area è una misura additiva. Anche il perimetro è una misura additiva ma si comporta in modo diverso da quello dell'area.
Link all'articolo: Togli un altro quadrato.
28 settembre 2023
[A23-43] Togli triangoli (1)
Questa griglia di 25 triangoli equilateri di lato unitario ha il perimetro uguale a 15.
Si può togliere un triangolo in modo da far aumentare il perimetro.
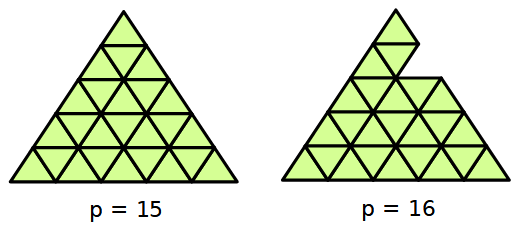
1) Continua a togliere triangoli, uno alla volta in modo da far aumentare al massimo il perimetro della figura. Quanti triangoli hai tolto?
2) Quante forme diverse di perimetro massimo si possono ottenere?
Precisazione. La forma ottenuta deve essere un poligono semplice: niente buchi, niente intrecci.
26 settembre 2023
[A23-42] Giuseppe Peano e le donne matematiche
Cercando notizie su Paolina Quarra, ho trovato questa fotografia che mi ha commosso.

Giuseppe Peano e le allieve delle Conferenze Matematiche Torinesi (1928).
---
Forse Paolina Quarra è una delle matematiche rappresentate nella foto ma non so qual è...
Peano, naturalmente, è il saggio con la barba, alquanto soddisfatto!
"Rosetta Frisone, Elisa Viglezio, Clementina Ferrero, Paola Quarra, Gilda Mori Breda, Tiziana Comi, Maria Destefanis, Tina Pizzardo, Luisa Viriglio, Fausta Audisio, Piera Chinaglia e Cesarina Rosa Boccalatte, impegnate nell’insegnamento secondario, parteciparono attivamente alle Conferenze matematiche torinesi, istituite da Peano, esponendo i loro risultati, alcuni dei quali furono poi, per suo tramite, pubblicati."
---
La foto e i nomi delle allieve di Peano sono tratti da: Silvia Roero, Erika Luciano, L’altra metà del cielo nella scienza italiana dal Settecento al Novecento. Ricerche e studi recenti, Quaderni di storia della Fisica n.18, 2013, Dipartimento di Matematica G. Peano, Università di Torino.
Si può scaricare da qsf0074.dvi (unito.it), in formato PDF.
22 settembre 2023
[A23-41] Note storiche sul Test di Bertoldino
Forse non tutti sanno che la prima idea e la prima collezione di problemi capziosi è di Paolina Quarra che faceva parte del numeroso gruppo di collaboratrici e collaboratori del matematico Giuseppe Peano negli anni 1913-1930.
Paolina Quarra pubblicò la sua raccolta nell'articolo Problemi capziosi, Bollettino di Matematica (A. Conti), 1919.
Una breve biografia di Paolina Quarra si trova in Numeri, Atomi e Alambicchi. Donne e Scienza in Piemonte dal 1840 al 1960, a cura di Erika Luciano e Clara Silvia Roero, 2008
---
Aggiornata la pagina: Il test di Bertoldino con alcune note storiche.
18 settembre 2023
[A23-40] Pons asinorum - Il ponte degli asini
Teorema. Gli angoli alla base di un triangolo isoscele sono uguali.
E' il primo teorema di una certa difficoltà della geometria piana. Puoi andare avanti solo dopo averlo capito bene.
La seguente dimostrazione di Pappo, ripresa poi da Coxeter, mi ha sorpreso davvero!
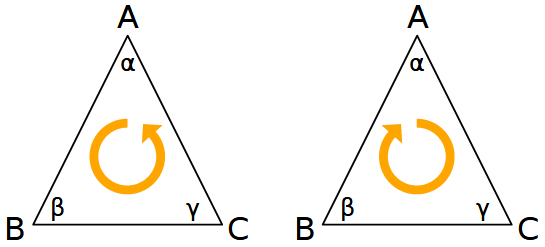
Partiamo dal triangolo isoscele ABC, con AB = CA.
Concepiamo mentalmente il triangolo ABC come se fosse due triangoli sovrapposti (dobbiamo percorrere i suoi vertici in senso orario e antiorario, ho disegnato due triangoli per facilitare l'immaginazione).
I due triangoli sono: ABC e ACB.
Per ipotesi hanno AB = AC e CA = BA.
Inoltre hanno CAB = BAC (angoli coincidenti)
Quindi i due triangoli sono uguali per il criterio lato-angolo-lato e in particolare hanno ABC = ACB ovvero: β = γ.
---
Coxeter, Harold Scott MacDonald, (1969, seconda edizione). Introduction to Geometry. John Wiley & Sons.
---
Spero di non aver sbagliato, altrimenti sono un asino.
13 settembre 2023
[A23-39] Links
Aggiornata la pagina dei Links
Cari amici, Internet sta scomparendo e quasi nessuno se ne accorge. Immagini, pagine, siti, portali, libertà e soprattutto persone se ne vanno giorno dopo giorno.
Lo percepiscono coloro che sono abbastanza vecchi come esploratori della rete: per esempio, io ho iniziato a esplorare il WEB con Netscape Navigator nel 1994, perciò ho circa 30 net-anni. Sembrano pochi ma sono tantissimi.
Ogni tanto aggiorno la pagina dei link e, a malincuore, ne devo
eliminare alcuni perché purtroppo non hanno più nulla da dire o non esistono
più.
Beh, però ne aggiungo qualcuno nuovo, anche se magari non è
proprio una novità!
TeX Live (compilatore LaTeX etc.)
HTML Notepad (editor visuale HTML portatile in meno di 4 Mb)
R (linguaggio di programmazione per la statistica e la grafica computazionali)
Ministero Educazione di El Salvador (si possono scaricare i libri di un intero corso di matematica dal 1° al 9° grado scolastico e molto altro)
Introduction to graph theory (un libro intero pubblicato da Darij Grindberg su arXiv)
Paper fortune teller (l'origami che ti dice il tuo futuro, articolo su Wikipedia)
Mathematical Spectrum (tutti i 144 numeri della rivista, dal 1968 al 2016)
Il link vietato (purtroppo non posso scriverlo perché è vietato)
E così via...
12 settembre 2023
[A23-38] La password (3)
Aggiornata la pagina Il lato comico.
Cari amici, abbiate pazienza ma devo concludere il tormentone della password con quest'altra barzelletta, per ora.
---
La nuova password
(chiedo scusa per eventuali parolacce, che ho cercato di moderare)
Ho perso la password per l'accesso ai servizi bancari e devo crearne una nuova.
Sullo schermo appare la scritta:
COMPUTER: Digita la nuova password, che deve essere diversa da quella precedente.
IO: palla
COMPUTER: La password è troppo corta, deve avere almeno 8 caratteri.
IO: palla di ercole
COMPUTER: La password è troppo debole, deve contenere almeno un numero.
IO: 2 palle di ercole
COMPUTER: La password non deve contenere spazi vuoti.
IO: 2pallediercole
COMPUTER: La password deve contenere almeno un carattere maiuscolo.
IO: 4PALLEdiErcole
COMPUTER: La password non deve contenere caratteri maiuscoli consecutivi.
IO: PerLe6PalleDiErcoleFammiEntrareStupidoComputer!
COMPUTER: La password non deve contenere segni di punteggiatura.
IO: PerLe8PalleDiHulkFammiEntrareStupidoComputerOppureTiDistruggo
COMPUTER: Password non valida perché uguale a quella precedente, che hai perso.
10 settembre 2023
[A23-37] La password (2)
Aggiornata la pagina Il lato comico.

9 settembre 2023
[A23-36] La password (1)
Aggiornata la pagina Il lato comico.
38. La password (1)
In un bar, a Genova.
Avventore: "Buongiorno, qual è la password del vostro Wi-Fi?"
Barista: "Si deve fare una consumazione per ottenere la password."
A: "Ok, una spuma al ginger, per favore."
B: "Sono 3 Euro."
L'Avventore paga, consuma e chiede: "Ora mi può dire qual è la password del vostro Wi-Fi?"
B: "Si deve fare una consumazione per ottenere la password."
---
P.S. Mi piacerebbe trovare una password più breve ma altrettanto espressiva. Se ve ne viene in mente una, fatemi sapere.
8 settembre 2023
[A23-35] AttivAzione Matematica
Segnalo a tutti i colleghi docenti di Matematica questo bel libro:
Antonella Castellini, Chiara Giberti, Alice Lemmo, Andrea Maffia, AttivAzione. Laboratori di matematica per la scuola del primo ciclo, Libreriauniversitaria.it, 2023.

Il libro presenta le 5 componenti dell'apprendimento matematico, seguendo le definizioni della ricercatrice Martha Isabel Fandiño Pinilla:
- apprendimento concettuale;
- apprendimento algoritmico;
- apprendimento di strategie;
- apprendimento comunicativo;
- apprendimento e gestione delle trasformazioni semiotiche.
Propone poi l'esplorazione di alcuni oggetti matematici attraverso attività di laboratorio chiamate "AttivAzioni".
Tutte le proposte sono strettamente legate alle Indicazioni Nazionali per il Curricolo del 2012.
Come esempio, mi piace citare il laboratorio sulle piramidi numeriche additive e in particolare il seguente esercizio, che riguarda l'apprendimento di strategie.
---
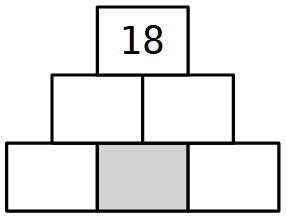
Esercizio 6. Scrivi nella casella grigia il numero naturale più piccolo che rende impossibile la piramide nell'insieme dei numeri naturali.
Spiega come hai ragionato.
7 settembre 2023
[A23-34] Perimetro massimo
20 esagoni di lato unitario formano una griglia esagonale di perimetro 30.
Si possono togliere, per esempio due esagoni in modo da ottenere una figura di perimetro 34.
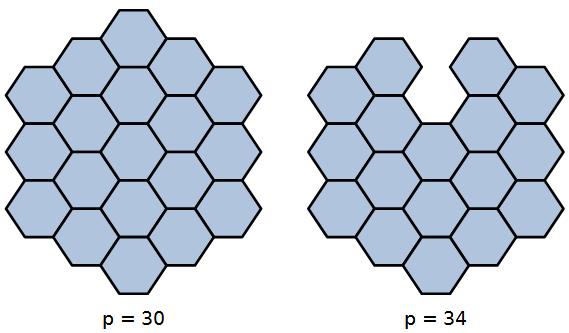
Quanti e quali esagoni si devono togliere affinché il perimetro della figura ottenuta sia il più lungo possibile?
La figura ottenuta deve essere un poligono semplice, cioè non deve avere buchi.
6 settembre 2023
[A23-33] Perimetro costante
Una griglia 3x3 di quadrati unitari ha area A = 9 e perimetro p = 12.
Si può togliere un quadrato in modo da ottenere una figura di area 8 e perimetro sempre uguale a 12.
Si può togliere un altro quadrato in modo che l'area sia 7 e il perimetro sempre 12.
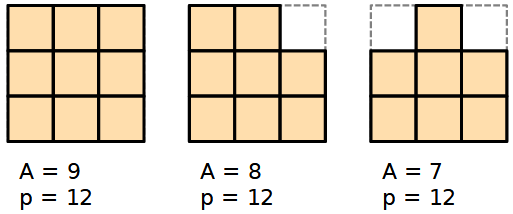
1) Quanti quadrati si possono togliere al massimo per ottenere una figura che ha il perimetro uguale a 12?
2) Quante figure finali diverse di area minima e perimetro 12 si possono ottenere con questo procedimento?
I quadrati che formano le figure devono avere almeno un lato in comune. Per esempio, la figura qui sotto non è una soluzione accettabile.
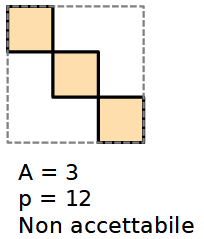
---
Ispirato da una serie di problemi pubblicati da James Tanton su X (ex Twitter).
5 settembre 2023
[A23-32] Ancora Bertoldino
Scale
In un palazzo di 7 piani, devi salire 20 scalini per andare da un piano al piano successivo.
Quanti scalini devi salire per andare dal primo al terzo piano?
10 euro in regalo
Aldo ha 10 € in tasca e chiede a sua
mamma altri 10 € in regalo.
Quanti euro avrà in tasca?
---
Aggiornata la pagina: Il test di Bertoldino.
5 agosto 2023
Agosto 2023
Cari amici di BASE Cinque,
vi auguro felici vacanze dovunque voi siate,
ai monti, al mare, in campagna, in città!
![]()
1 agosto 2023
[A23-31] Piante preistoriche che non seguivano la sequenza di Fibonacci
Un articolo da ricordare per investigazioni future.
Turner H. A., Humpage M., Kerp H., Hetherington A. J. Leaves and sporangia developed in rare non-Fibonacci spirals in early leafy plants.
Science. 2023, Jun 16.
La maggior parte delle piante esistenti oggi mostra schemi fillotattici descritti matematicamente dalla sequenza di Fibonacci.
Gli autori hanno scoperto che la fillotassi nei fossili del licopode del Devoniano inferiore, Asteroxylon mackiei non seguiva la sequenza di Fibonacci. Siamo a circa 400 milioni di anni fa.
I risultati della ricerca fanno luce sulle origini delle foglie e dimostrano l'antichità delle spirali non di Fibonacci nelle piante.
25 luglio 2023
[A23-30] Scissor congruence
Beh, ho imparato che scissor congruence è un termine tecnico.
Potremmo tradurlo in italiano provvisoriamente "congruenza delle forbici"?
Quale potrebbe essere una traduzione migliore?
---
Definizione. Due poligoni sono scissor congruent se è possibile tagliare in pezzi uno dei due poligoni con un paio di forbici e sistemare i pezzi in modo da formare l'altro poligono.
Queste forbici fanno soltanto tagli rettilinei.
---
Esercizio. Dimostrare che i quattro poligoni della figura qui sotto sono scissor congruent.
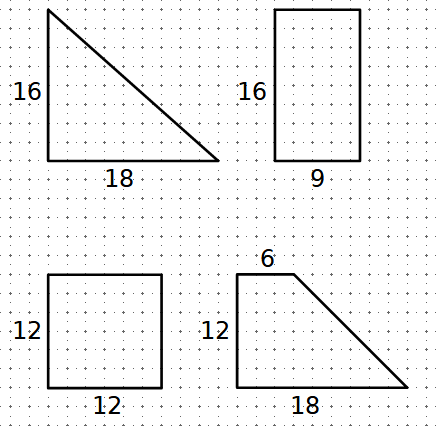
26 giugno 2023
[A23-29] Un piccolo mistero su un libro di Alexander Abian

Ultimamente ho potuto confrontare l'edizione inglese con quella italiana del libro sugli insiemi di Abian:
- Alexander Abian, The Theory of Sets and Transfinite Arithmetic, Saunders, 1965.
- Alexander Abian, La teoria degli insiemi e l'aritmetica transfinita, Feltrinelli, 1972.
L'edizione inglese di questo libro è di circa 400 pagine mentre l'edizione italiana citata è di circa 800 pagine.
E' lunga il doppio. Come si spiega?
Nella prefazione all'edizione italiana, Abian dichiara di aver ampliato il libro per motivi pedagogici, per correggere errori e per aggiornare il contenuto ai risultati più recenti della ricerca matematica.
Esprime inoltre gratitudine alla traduttrice Giulia Maria Piacentini Cattaneo per il suo abile lavoro.
Ora capisco meglio perché questo libro ha una marcia in più. Però non sono riuscito a trovare altri riferimenti all'edizione italiana.
22 giugno 2023
[A23-28] Il più bel libro di matematica per l'università
Nel passaggio dalla scuola superiore alla facoltà di Matematica feci un'esperienza didattica per me negativa: i libri di testo e le lezioni dei vari corsi presupponevano che io conoscessi già i fondamenti delle teorie matematiche e capissi da solo le motivazioni del loro sviluppo.
Per esempio, i corsi di Analisi matematica presentavano in modo affrettato e lacunoso la fondazione dei numeri reali. Inoltre seguivano almeno due strade completamente diverse.
I libri di Topologia erano una sequenza di assiomi-definizioni-teoremi senza spiegare perché si era scelta quella strada piuttosto che un'altra.
Ma il caso più eclatante è stata la teoria degli insiemi. Praticamente tutti i corsi di Algebra, Analisi, Topologia, davano per scontata la teoria degli insiemi o ne presentavano rapidamente una versione "ingenua". No buono!
Il libro (scolastico) più bello e utile per me è ancora oggi La teoria degli insiemi e l'aritmetica transfinita di Alexander Abian, pubblicato nel 1972 da Feltrinelli.
La traduzione in italiano di Giulia Maria Piacentini Cattaneo è fenomenale!
Ma è solo una traduzione o è invece qualcosa di più?
E pensare che il matematico iraniano Alexander Smbat Abian è diventato famoso come "il professore che voleva distruggere la Luna".

Alexander Abian (1923-1999)
16 giugno 2023
[A23-27] Manifesto per la didattica della Matematica
Cari amici, Francis Su, con il suo libro Mathematics for human flourishing del 2020 ci ha di-mostrato come la Matematica è collegata con i desideri e i bisogni più importanti degli esseri umani.
Ha senso studiare la Matematica perché ti aiuta a realizzare i tuoi bisogni di esplorazione, gioco, collaborazione, immaginazione, libertà, combattimento e così via, fino alla verità, alla bellezza e all'amore.
Noi insegnanti conosciamo bene la Matematica come struttura di discipline e ora possiamo vederla lucidamente anche come struttura di belle emozioni che spingono a studiarla. Dovremmo lavorarci prima nei nostri cuori e poi trasferire questa visione anche nel nostro lavoro a scuola.
Queste idee stanno emergendo in Italia già da molti anni, come si vede dalla bibliografia qui sotto.
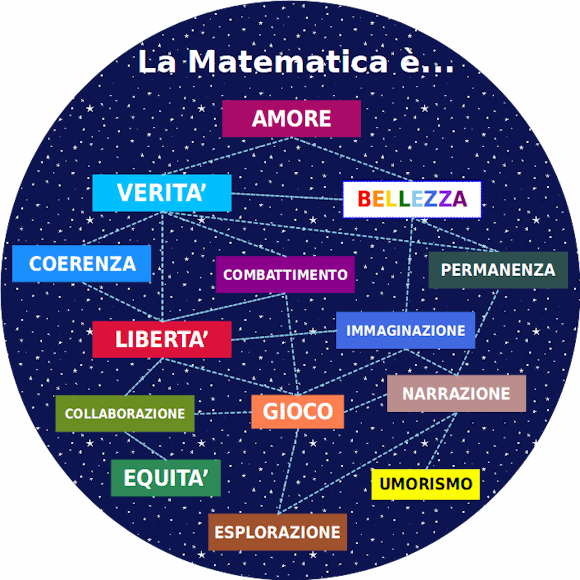
---
- Libertà
Carimali, Lorella (2020). L’equazione della libertà. Rizzoli.
Marini, Claudio (2019). Matematica d’evasione. 20 facili lezioni da un’esperienza di insegnamento in carcere. libreriauniversitaria.it - Narrazione
Lolli, Gabriele (2018). Matematica come narrazione. Il Mulino. - Umorismo
Lolli, Gabriele (1998). Il riso di Talete: matematica e umorismo. Bollati Boringhieri. - Bellezza
Filocamo, Giovanni (2017). La matematica è un’opera d’arte. I numeri e le formule che ispirano la bellezza. Gribaudo. - Gioco
Filocamo, Giovanni (2022). La matematica si impara giocando. Curiosità e giochi di intelligenza pensati per chi (non) ama la matematica. Gribaudo. - Esplorazione
Sabatti, Sofia (2020). Diario di bordo. Una prof di matematica nell’anno del lockdown. Mateinitaly.
Spero che l'elenco dei libri si espanda!
14 giugno 2023
[A23-26] Godel e il tempo
Aggiornata la pagina Il lato comico.
37. Godel e il tempo
In un dialogo di circa 3 anni fa, Godel mi disse che il tempo non conta nella logica, tranne che nelle logiche temporali.
Qui l'ho messo alla prova, e si è arrabbiato di nuovo.

12 giugno 2023
[A23-25] (Quasi) tutti i numeri razionali sono periodici
Cari amici, siete davvero convinti, certi, sicuri che 0,(9) periodico sia uguale a 1?
0,(9) = 0,9999999999... = 1?
Esistono decine di filmati e articoli (anche scientifici) che tentano di convincere la gente che questa uguaglianza è vera. Alla lunga, potrebbe sembrare che questo sia un caso unico, eccentrico, particolare.
La verità è che tutti i numeri razionali si possono rappresentare come numeri decimali periodici.In particolare, i numeri interi e i decimali finiti hanno due rappresentazioni decimali di cui una è periodica con periodo 9
Per esempio:
2 = 1,999...
35 = 34,999...
0,75 = 0,74999...
86,9 = 86,8999...
Solo il numero 0 se ne sta fuori da questi giochi.
0 = 0
---
Letture di approfondimento.
1) Se volete capire PERCHE' 0,(9) = 1:
Anatriello, G., & Vincenzi, G. (2019). On the definition of periodic decimal representations: An alternative point of view. The Mathematics Enthusiast, 16(1–3), 3–14.
2) Se invece volete capire QUANDO 0,(9) < 1:
Katz, K. U., & Katz, M. G. (2010). When is .999. . . less than 1? The Mathematics Enthusiast, 7(1), 3–30.
6 giugno 2023
[A23-24] Trova l'intruso
Cari amici, ho trovato questa domanda sul gruppo FB Matematica & aneddoti.
---
TROVA L'INTRUSO
Nella seguente lista di numeri c'è un intruso.
Secondo te, qual è il numero intruso e perché?
11, 15, 92, 65
---
In questo tipo di domande c'è una grande libertà di risposta.
L'importante è usare tutte le proprie conoscenze per motivare la propria risposta. Così lo scambio di idee diventa molto istruttivo per tutti.
31 maggio 2023
[A23-23] Hao Wang

Hao Wang, nel lontano 1960 scrisse un articolo di logica matematica quasi fantascientifico: Proving Theorems by Pattern Recognition (parte I e II).
Nella prima parte dell'articolo descrive un programma per computer, capace di dimostrare automaticamente tutti i teoremi dei primi 9 capitoli dei Principia Mathematica in meno di 9 minuti. Sono 350 teoremi completi di dimostrazioni.
Afferma però che tale risultato è solo una "nocciolina" rispetto alle potenzialità di quel programma.
Il programma si chiamava semplicemente P, girava sul
computer IBM 704, era scritto in SAP Assembler,
memorizzato in 3200 schede perforate e occupava
13000 "words" di memoria. Una "word" nell'IBM 704 corrispondeva a
36 bit, quindi il programma impegnava circa 58,5 kb.
Nei nostri
telefonini Android, l'applicazione che accende e spegne la torcia occupa
circa 7 Mb = 7000 kb di memoria. Mi chiedo cos'altro fa.
---

L'altro motivo, non riportato nel ritaglio, è ancora più interessante...
Wang, H. (1960). Proving theorems by pattern recognition I. Communications of the ACM, 3(4), 220–234.
---
24 maggio 2023
[A23-22] Pensiero laterale geometrico
Dividete la figura in 6 pezzi congruenti, cioè identici per forma e dimensione. Attenzione... pensiero laterale.
Trovate due soluzioni.
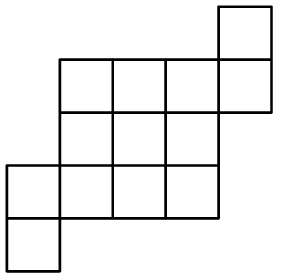
Un problema molto istruttivo postato da Dario Uri su Facebook, non andate a vedere la soluzione.
C'è anche una soluzione alternativa proposta da Livio Zucca.
21 maggio 2023
[A23-21] La mono-pastrella aperiodica "einstein"
Questo è un piccolo appunto su come costruire il poligono chiamato
"einstein" partendo da tre esagoni.
(ein Stein in tedesco significa "una
pietra" o "mattone" o "pedina")
Con questa unica piastrella si può tassellare il piano in modo aperiodico però gli autori usano anche la sua simmetrica, come si vede nell'esempio.
Quindi in realtà le piastrelle sarebbero 2.
Ma sono congruenti.
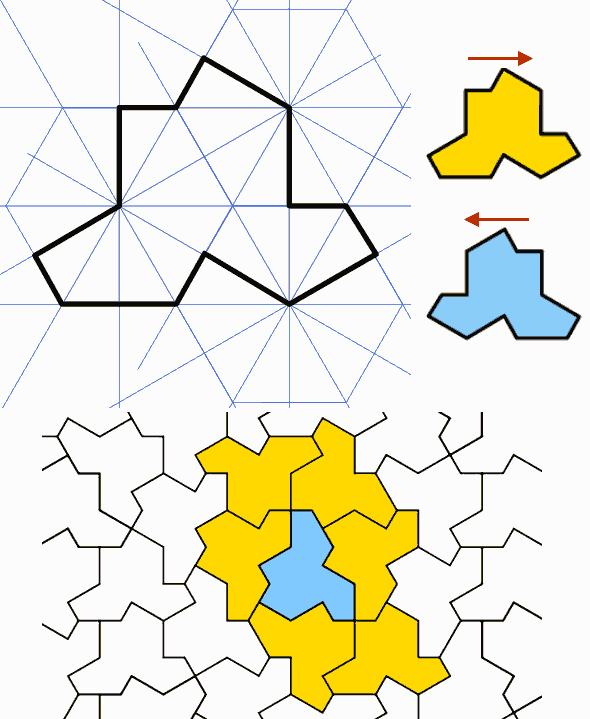
David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim
Goodman-Strauss,
An aperiodic monotile,
arXiv, 2023
19 maggio 2023
[A23-20] Di parabola ce n'è una sola
Qualunque parabola può trasformarsi in un'altra parabola soltanto con un cambiamento di scala.
Quindi tutte le parabole sono la stessa parabola vista sotto ingrandimenti diversi.
Stessa cosa vale per la circonferenza.
Invece non vale per le ellissi e le iperboli.
Che poi tutte queste curve sarebbero sezioni coniche.
Da meditare...
E anche da dimostrare.
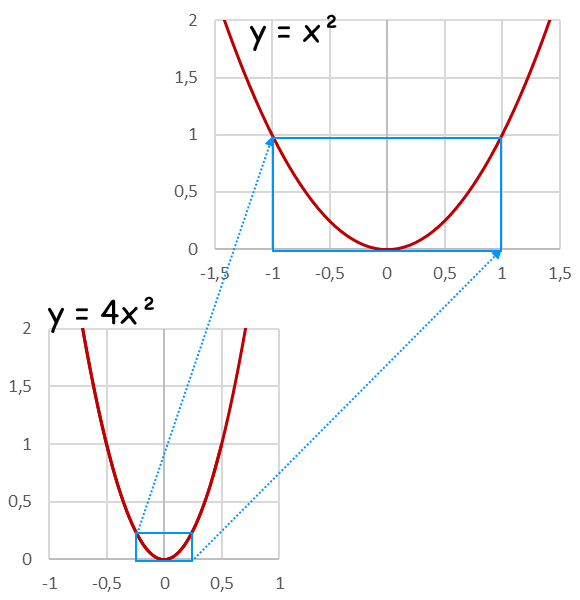
15 maggio 2023
[A23-19] Trisezione dell'angolo, senza parole
Roger B. Nelsen,
Proofs without words: Exercises in Visual Thinking,
Mathematical Association of America, Washington, 1993.
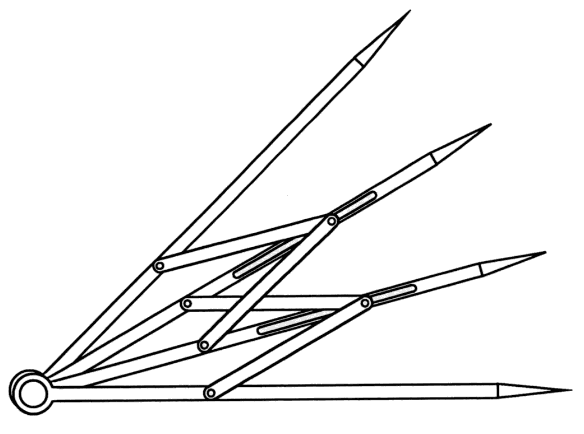
Roger Nelsen attibuisce questa dimostrazione senza parole a Rufus Isaacs.
Come si potrebbe dimostrare che questo dispositivo triseca un angolo e quali ipotesi dobbiamo aggiungere alla figura?
E... chi era Rufus Isaac?
16 aprile 2023
[A23-18] Icone della matematica
Mi piace l'idea di questo libro:
Claudi Alsina, Roger B. Nelsen,
Icons of Mathematics. An Exploration of Twenty Key Images,
The Mathematical Association of America, 2011.
A ciascuna icona è dedicato un capitolo con approfondimenti storici ed esplorazioni matematiche davvero interessanti.
Per esempio, perché quel classico caso del teorema di Pitagora si chiama "The Bride's Chair" (la poltrona della sposa)?
![]()
Sarebbe interessante estendere l'idea anche all'Aritmetica e all'Algebra elementari. Magari le icone potrebbero diventare 100.
2 aprile 2023
[A23-17] Links
AoPS - Art of Problem Solving - Forums
AoPS - Matematica per gradi scolastici
https://artofproblemsolving.com/community
AoPS - Gare Matematiche
https://artofproblemsolving.com/community/c13_contests
27 marzo 2023
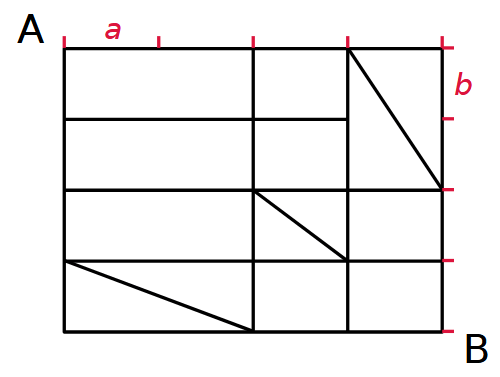
[A23-16] Percorsi minimi
Versione facile
Nello schema seguente, quanti sono i percorsi minimi da A a B?
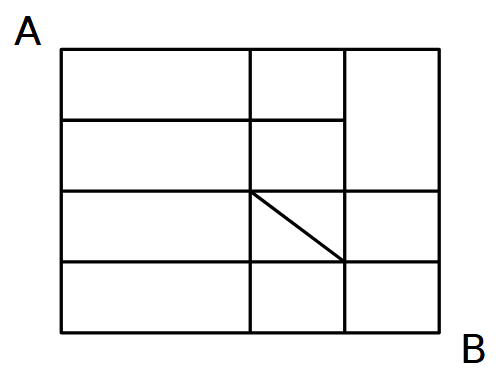
Versione difficile
Se aggiungiamo 2 strade come indicato nella figura, qual è il percorso minimo da A a B?
Da cosa dipende?
22 marzo 2023
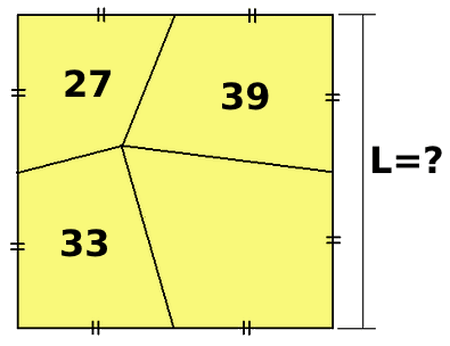
[A23-15] Lato del quadrato
Livio Zucca ha postato su FB il problema seguente. Mi ha sorpreso una soluzione assolutamente elementare.
---
Date le tre aree, trovare il lato del quadrato.
16 marzo 2023
[A23-14] Il progresso secondo qualcuno
Thor, un personaggio del mondo di B.C. di Johnny Hart, prima inventa la ruota rotonda, poi la migliora facendola quadrata per evitare che rotoli via da sola.
Ma quattro sobbalzi a ogni giro sono fastidiosi perciò migliora la ruota quadrata facendola triangolare perchè così c'è un sobbalzo in meno.
Ecco, questo è il tipo di progresso in ci vogliono far credere i sovrani di questo mondo.

Aggiornata la pagina del Lato comico.
14 marzo 2023
[A23-13] Stancamente pi...
Oggi, una parte dell'umanità celebra stancamente il pi-day, il giorno di un numero reale che si chiama pi greco. Dicono che è il rapporto fra la lunghezza di una circonferenza e quella del suo diametro.
Tutti felici sotto l'ombrello del calendario inglese, senza il quale non avremmo questo giorno.
In questi tempi, una parte dell'umanità ha almeno una cosa in comune con pi greco: l'irrazionalità.
Cari amici, vi invito tutti il 22 luglio a festeggiare un pi greco più razionale, calendario italiano, se tutto andrà bene...
13 marzo 2023
[A23-12] Ancora Bertoldino
Dal Forum e da FB, grazie a Quelo e Dario Uri.
Sette fratelli
Una donna ha 7 figli e metà di loro sono maschi.
Com'è possibile?
Due monete
Ho in tasca due monete la cui somma è di 3 euro.
Una delle monete non è una moneta da 2 euro.
Quali sono le monete?
Sottrarre 8
Quante volte si può sottrarre 8 da 64?
Quanti e ci sono?
Nella frase seguente, sostituisci i puntini in modo ottenere una affermazione giusta. Scrivi i numeri in lettere.
“In questa frase ci sono ... e.”
Mesi con 28 giorni
In un anno non bisestile, quanti sono i mesi con 28 giorni?
---
Aggiornata la pagina: Il test di Bertoldino.
10 marzo 2023
[A23-11] PUZZLE LETTER
Segnalo con piacere che Samuel Foster ha pubblicato sul numero di gennaio della sua PUZZLE LETTER (https://puzzleletter.com/solved/1#temple) il problema Sangaku 4 che si trova su BASE Cinque, con la risoluzione di Antonio Palladino assieme ad alcune integrazioni.
Ringrazio Samuel Foster e auguro prosperità alla sua iniziativa.
6 marzo 2023
[A23-10] Ancora problemi capziosi
Ultimamente sto incontrando diversi problemi capziosi. Eccone altri tre.
Somma delle età
Quest'anno, la somma delle età di Greta, Sofia e Martina è 29 anni.
Quale sarà la somma delle loro età l'anno prossimo?
Mezzo bicchiere
Un bicchiere pieno d'acqua pesa 200 grammi.
Quanto pesa il bicchiere pieno a metà?
Collezionatori
In una classe, 15 alunni collezionano figurine, 5 alunni collezionano biglie e i restanti 6 alunni non collezionano nulla.
Quanti sono in tutto gli alunni della classe?
---
Aggiornata la pagina: Il test di Bertoldino.
27 febbraio 2023
[A23-9] Cruciverba aritmetico minimo
Quante soluzioni ha il seguente cuciverba?

Orizzontali
1. E' un numero primo.
3. E' quadrato perfetto.
Verticali
1. E' un numero primo.
2. E' un quadrato perfetto.
Note.
Il risultato di ogni definizione deve essere un numero di due cifre che non inizia per 0.
I risultati delle 4 definizioni devono essere numeri tutti diversi.
---
Tratto (con modifiche) dalle Junior Mathematic Olympiad - 2021 (https://www.ukmt.org.uk/).
20 febbraio 2023
[A23-8] Un puzzle di David Singmaster sulle grate
Grazie a questo puzzle di David Singmaster ho notato e iniziato a studiare le grate a occhio bottato, diffuse e costruite ancora oggi in Liguria e in tutta Italia.

Ci sono grate "impossibili" nelle stampe Cycle (1933) e Belvedere (1968) di Maurits Cornelis Escher.
- Come si possono rappresentare matematicamente queste grate?
- Come si fa a distinguere una grata "possibile" da una "impossibile"?
---
Vedi: David Singmaster, About puzzle grills, presentato al Maths Jam Gathering del 2015.
13 febbraio 2023
[A23-7] David Singmaster
Un mio piccolo ricordo di David Singmaster, con tanta gratitudine.

David Breyer Singmaster, nato nel 1938, ci ha lasciati il 13 febbraio 2023. Che la sua anima riposi in pace nella luce eterna.
La sua opera che mi guida sempre nel territorio della Matematica ricreativa è:
Sources in Recreational Mathematics - An annotated bibliography.
Reperibile qui: https://www.puzzlemuseum.com/singma/singma-index.htm
5 febbraio 2023
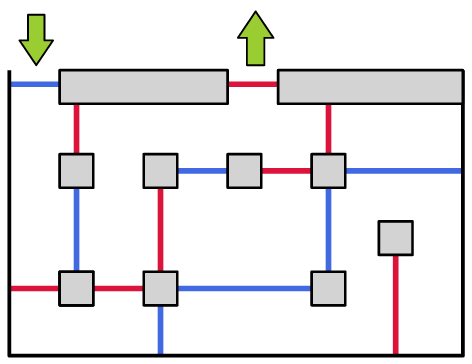
[A23-6] Labirinto blu e rosso
Entra nel labirinto dalla porta blu e trova il percorso per uscire dalla porta rossa.
Regola. In questo labirinto devi attraversare alternativamente una porta blu, una rossa, una blu, una rossa, e così via. In altre parole non puoi attraversare di seguito due porte dello stesso colore.
Le linee nere rappresentano muri e non si possono attraversare.
29 gennaio 2023
[A23-5] Altri due problemi capziosi
Biglietti
Su un tavolo ci sono dei biglietti numerati da 10 a 30.
Entrano alcuni ragazzi e ciascuno prende un biglietto.
Alla fine rimangono 3 biglietti sul tavolo.
Quanti sono i ragazzi?
In ordine di altezza
Alcuni giocatori di pallacanestro sono in fila, disposti in ordine di altezza.
Se partiamo dal più alto, Andrea si trova all'11° posto della fila.
Se invece partiamo dal più basso, Andrea si trova al 9° posto.
Quanti sono i giocatori in fila?
---
Aggiornata la pagina: Il test di Bertoldino.
22 gennaio 2023
[A23-4] Il resto del giornalaio
Federico è andato dal giornalaio con 5 monete da 1 € in tasca per comprare il suo giornalino preferito.
Il giornalaio gli chiede 3,50 €.
Quanto riceve Federico di resto?
---
Aggiornata la pagina: Il test di Bertoldino.
---
Nota.
Tratto da Emanuele Fiorini, Enigmi e illusioni, Armando Editore, 2004.
15 gennaio 2023
[A23-3] Il foglio strappato
Un foglio viene strappato da un libro.
La somma dei numeri di pagina scritti sui fogli rimanenti
del libro è 15000.
Quali erano i due numeri di pagina scritti sul foglio strappato?
---
Variante 1.
La somma di numeri di pagina scritti sui fogli successivi a quello strappato è 15000.
Quali erano i due numeri di pagina scritti sul foglio strappato?
Variante 2.
La somma di numeri di pagina scritti sui fogli precedenti a quello strappato è 15000.
Quali erano i due numeri di pagina scritti sul foglio strappato?
---
Note.
1. Ogni foglio comprende due pagine.
2. La numerazione inizia col primo foglio che porta i numeri 1, 2 e termina con l'ultimo foglio.
3. I fogli della copertina non portano numeri.
4. Il problema è tratto dalle Olimpiadi Regionali di Matematica, India, 1994.
8 gennaio 2023
[A23-2] Fourier vs Courier
Aggiornata la pagina: Umorismo matematico.
Visto su Reddit e modificato un po'.
1 gennaio 2023
[A23-1] Buon anno!
Cari amici, buon anno a tutti!
Auguro che un sole sorridente come questo porti calore e allegria nei vostri cuori per tutto il 2023.

Grazie Bruno!