30 dicembre 2020 - 365.2020[BASE Cinque - Appunti di Matematica ricreativa]
30 dicembre 2020 - 365.2020
Addio 2020
Cari amici, ecco una breve sintesi del labirintico 2020.
Sto pensando a un augurio per il 2021.
Arrivederci all'anno prossimo!
25 dicembre 2020 - 360.2020
Natività 2020 - Mato Grosso - Buon Natale a tutti!
20 dicembre 2020 - 355.2020
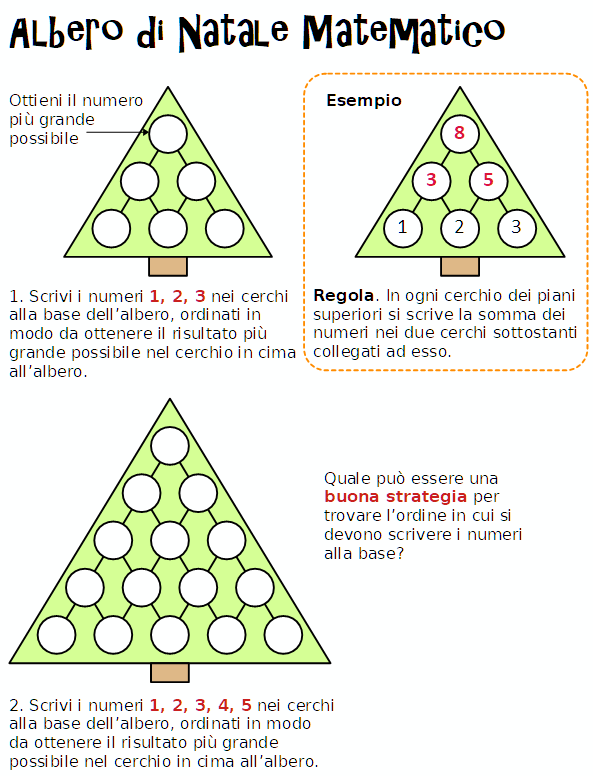
Albero di Natale matematico
Cari amici, auguro a tutti voi e ai vostri cari, buon Natale di Gesù, un 2021 sereno e soprattutto pace e bene!
E se vi piace, molta buona matematica.
15 dicembre 2020 - 350.2020
Chi è quel matematico?
E' stato un matematico molto conosciuto dal grande pubblico per i suoi libri di enigmi logici. Musicista e anche un po' mago.
Riuscite a individuarlo basandovi sulla somiglianza con i suoi ritratti più diffusi?
---
La foto, del 1968, è tratta dall'archivio di Paul Halmos, il matematico che fotografava i matematici.
10 dicembre 2020 2020 - 345.2020
Finalmente possiamo slegare la capra!
Immagina un pascolo racchiuso da un recinto perfettamente circolare di raggio 100.
Dentro il pascolo si trova una capra legata in un punto del recinto con una corda lunga x.
Che lunghezza deve avere la corda affinché la capra possa mangiare l'erba di mezzo pascolo?
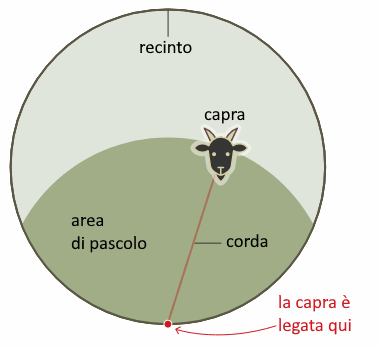
Si può trovare facilmente una soluzione approssimata di questo problema ma nessuno era ancora riuscito a trovarne la soluzione esatta.
A quanto pare, il matematico Ingo Uillisch è riuscito in questa impresa, come riportato sul Quanta Magazine (Mathematician Solves Centuries-Old Grazing Goat Problem Exactly | Quanta Magazine).
Sembra strano, ma il problema con la capra legata esternamente al recinto è più facile. Come è pure più facile la versione a 3 dimensioni, con un uccellino legato invece della capra.
5 dicembre 2020 - 340.2020
Numeri in giostra per Natale
Scrivete i numeri nei cerchi vuoti.
---
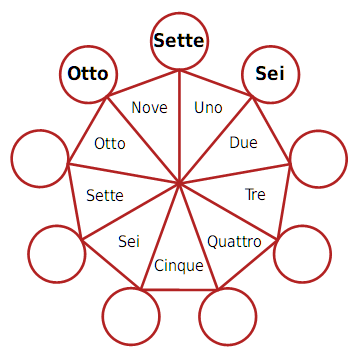
Grazie a Bruno per questo bel puzzle numerico inviato al Forum.
30 novembre 2020 - 335.2020
Un problema di 4000 anni fa, fresco come una rosa appena colta
Gli alunni babilonesi, nel 1900 a. C., non usavano i quaderni ma i tablet, cioè le tavolette di argilla. Come compito per casa ricevevano una tavoletta su cui era scritto un esercizio.
Ecco un esempio di problema geometrico antichissimo e modernissimo.
---
La figura è formata da tre trapezi isosceli congruenti, uniti in modo da formare una fascia triangolare limitata da due triangoli equilateri.
Il perimetro del triangolo esterno ABC misura 90 cm.
Il perimetro del triangolo interno DEF misura 30 cm.
a) Calcola l'area di ciascun trapezio.
b) In quanti modi si può risolvere?
---
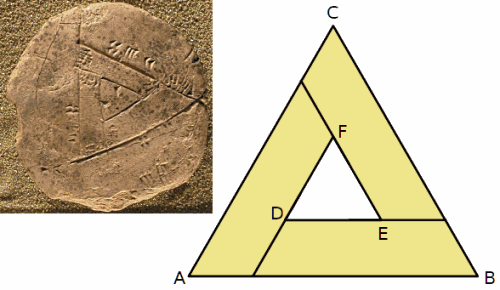
Tratto dal libro di Jöran Friberg, A Remarkable Collection of Babylonian Mathematical Texts, Springer.
23 novembre 2020 - 328.2020
IL FIBONACCI di Franco Conti
Cari amici, in questo giorno dedicato a Fibonacci mi piace ricordare i mitici poster di Franco Conti.
Vi propongo un esercizio facile tratto dal foglio n. 2.
"IL FIBONACCI è una raccolta di nove "fogli" creati tra il 1990 e il 2004 da Franco Conti, talvolta assieme ad alcuni collaboratori, in occasione della finale nazionale delle Olimpiadi della Matematica. Ciascun foglio contiene curiosità, idee, problemi e aneddoti di carattere matematico. Si propone di stimolare curiosità su aspetti insoliti o nascosti della matematica e si rivolge a tutti coloro che trovano gusto nell’affrontare problemi matematici, anche complessi."
---
Dal volume IL FIBONACCI - Breve viaggio fra curiosità matematiche, a cura di Edoardo Sinibaldi, Unione Matematica Italiana, 2011.
Per il Fibonacci day, 23/11/2020.
20 novembre 2020 - 325.2020
Altri problemi capziosi
Nota. Secondo le statistiche, un essere umano a 2 anni è alto circa la metà di quanto lo sarà da adulto.
15 novembre 2020 - 320.2020
Test di gruppo per il coronavirus?
Credevo che fosse solo un gioco matematico ma, a quanto pare, la stessa procedura è usata per scoprire i casi positivi molto velocemente, non solo per il COVID-19.
Ecco il problema di matematica ricreativa.
---
La bottiglia avvelenata.
Hai 100 bottiglie di vino, due delle quali sono avvelenate.
Esiste un test per scoprire se un campione di vino è avvelenato, che funziona così: metti una goccia di reagente in un bicchiere di vino. Se il vino diventa verde, allora contiene veleno.
Vuoi scoprire quali bottiglie sono avvelenate facendo il minor numero possibile di test.
Il problema si può risolvere, per esempio, facendo circa 20 = 2×√100 test.
Come?
---
Riporto due figure tratte dall'articolo di David Austin, Pooling strategies for COVID-19 testing, pubblicato su AMS (http://www.ams.org/publicoutreach/feature-column/fc-2020-10).
---
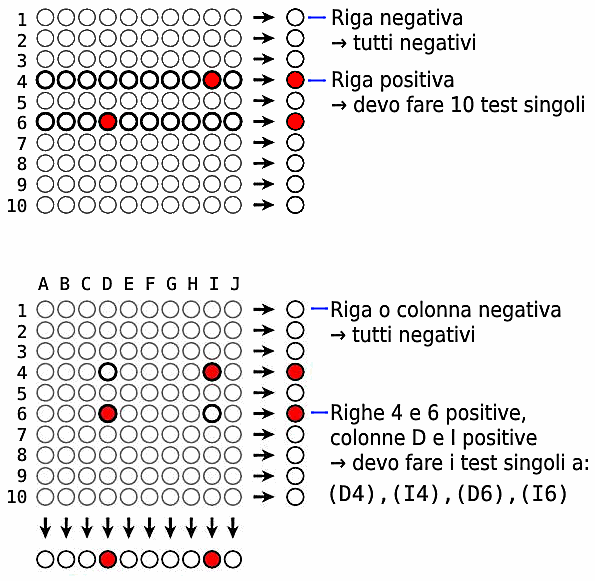
L'idea è questa: invece di testare tutte le 100 bottiglie individualmente, le divido in 10 gruppi di 10 bottiglie ciascuno e faccio il test a ogni gruppo. In altre parole, prelevo un po' di vino da ciascuna delle 10 bottiglie e verso tutti i prelievi in un unico bicchiere. Poi faccio il test.
Se è negativo, allora tutte le bottiglie del gruppo sono buone.
Se è positivo, allora nel gruppo c'è almeno una bottiglia avvelenata. Per trovarla devo fare 10 test individuali alle bottiglie del gruppo.
La seconda figura mostra come migliorare la strategia usando le coordinate cartesiane.
Ok, diciamo che il metodo funziona bene se la percentuale dei positivi è bassa.
10 novembre 2020 - 315.2020
La matematica delle cimici
Nei luoghi dove fa un po' più freddo, le cimici si rifugiano nei soffioni (infruttescenze del tarassaco), come si vede nella foto qui sotto. Riescono a entrare senza staccare neanche una piuma. Magari si dànno appuntamenti galanti.
E' un rifugio che dura poco: oggi c'è e domani non c'è più.
Questa scena ha attirato la mia attenzione. L'ho fotografata e continuavo a osservare la foto perché mi pareva che ci fosse qualcosa di matematico, ma sfuggente.
Soffione piccolo, 1 cimice.
Soffione grande, 2 cimici.
Poi ho pensato: anche il rapporto tra i volumi dei soffioni è forse 1:2?
Ho preso qualche misura sulla foto, però... che forma ha il soffione, e come si calcola il suo volume?
Se lo approssimiamo a una sfera, il rapporto è un po' maggiore di 1:2.
Ma si vede che è una sfera schiacciata, forse un ellissoide.
Sono capace di calcolare il volume di un ellissoide? Sì, la formula assomiglia a quella della sfera.
In questo caso, il rapporto tra i volumi dei due soffioni è circa 1:2.
Wow, le cimici sanno la matematica e si distribuiscono nei soffioni proporzionalmente ai volumi.
Ma la forma del soffione non è proprio un ellissoide.
So descrivere meglio geometricamente la forma del soffione? No!
So calcolare il volume di tale forma? No!
Le cimici invece lo sanno.
Ecco, ho molto da studiare sulla forma del soffione.
Questa, per me, è stata una lezione di umiltà matematica.
5 novembre 2020 - 310.2020
Tom Lehrer rilascia nel pubblico dominio tutte le sue canzoni (parole e spartiti musicali)
Thomas Andrew "Tom" Lehrer (1928) è il matematico, cantautore e pianista statunitense noto per le sue esilaranti canzoni ispirate ad argomenti di matematica e scienze (e altro).
Si può scaricare tutto qui: Songs and Lyrics by Tom Lehrer.
Ma attenzione, dovete affrettarvi perché il sito sarà chiuso il 31 dicembre 2024! (non è un fattoriale).
THAT'S MATHEMATICS
words and music by Tom Lehrer
Counting sheep --- when you're trying to sleep,
Being fair --- when there's something to share,
Being neat --- when you're folding a sheet,
That's mathematics!
When a ball --- bounces off of a wall,
When you cook --- from a recipe book,
When you know --- how much money you owe,
That's mathematics!
...
Su YouTube si trovano molti filmati di Tom Lehrer, per esempio: That's Mathematics, New Math, Lobachevsky.
31 ottobre 2020 -
305.2020
Meditazioni su una pallina nel labirinto
Per due soldi, ho trovato un gioco della pallina-nel-labirinto diverso dai soliti.
Aiuta a capire cosa succede quando ci si ostina a sbattere la testa contro gli ostacoli. Ma anche che arrivare al traguardo non è poi così difficile come sembra. Dipende da qual è il traguardo.
A parte gli scherzi, in questo tipo di labirinti i tranelli e i muri di solito sono fissi. In questo, invece, non ci sono tranelli ma 20 cubi e 10 cilindri che si muovono ostacolando la pallina. Anzi, sei tu che li muovi mentre provi a portare la pallina al traguardo. E fanno praticamente gli stessi movimenti della pallina.
Ma sono rallentati dall'attrito e imprigionati nelle loro caselle.
Come si potrebbe modificare questo gioco per renderlo più difficile?
26 ottobre 2020 -300.2020
Gianni Rodari e la matematica
Gianni Rodari, nel suo libro Grammatica della fantasia parla anche di matematica, in due parti che hanno titoli simmetrici.
---
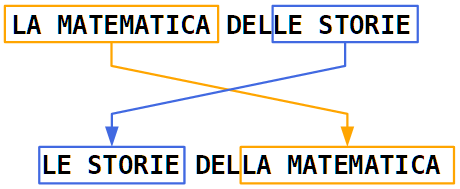
Nota cronologica doverosa: la fiaba del brutto anatroccolo fu pubblicata nel 1843 mentre il primo scritto di Cantor sulla teoria degli insiemi è del 1874. Perciò Andersen non poteva pensare quella fiaba in termini insiemistici cantoriani. Ma ciò non ha importanza.
---
Paolo Alessandrini ha pubblicato nel suo blog Mr. Palomar, una serie di articoli dedicati alla matematica di Gianni Rodari.
21 ottobre 2020 - 295.2020
Dedicato a Gianni Rodari
Cari amici, fissate per circa 15 secondi la crocetta bianca sul naso del ritratto che vedete qui sotto.
Spostate poi gli occhi sulla parete del muro di fronte a voi.
Sbattete un po' le palpebre.
Vi apparirà il volto di Gianni Rodari in positivo su fondo giallo.
L'illusione ottica si basa sulle "after images" di cui parlo qui: Un signore con la barba.
Quanti pesci ci sono nel mare?
Tre pescatori di Livorno
disputarono un anno e un giorno
per stabilire e sentenziare
quanti pesci ci sono nel mare.
Disse il primo: “Ce n’è più di sette,
senza contare le acciughette”.
Disse il secondo: “Ce n’è più di mille,
senza contare scampi ed anguille”.
Il terzo disse: “Più di un milione!”.
E tutti e tre avevano ragione.
La poesia è tratta da Gianni Rodari, Filastrocche in cielo e in terra.
16 ottobre 2020 - 290.2020
Cubo rosso
Sono dati otto cubi uguali. Un terzo del totale delle loro facce sono blu, il resto sono rosse.
Usando questi cubi, abbiamo costruito un cubo più grande in modo che esattamente un terzo della sua superficie sia rosso.
Dimostrare che è possibile usare gli stessi cubi per costruire un cubo grande la cui superficie sia interamente rossa.
---
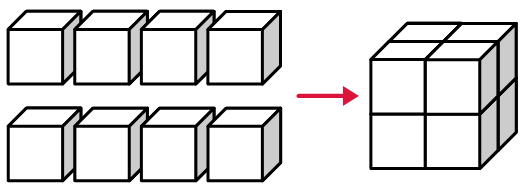
Questo problema è interessante perché a prima vista sembra difficile controllare le moltissime disposizioni possibili. Tuttavia basta una piccola illuminazione per risolverlo con pochi calcoli mentali e un semplice ragionamento...
---
Tratto dal Tanya Khovanova's Math Blog al quale siamo molto affezionati. Grazie a Panurgo per averlo proposto al Forum.
11 ottobre 2020 - 285.2020
Le figure impossibili di Oscar Reutesvard
In questo bel libro di Bruno Ernst ci sono i modelli di carta da ritagliare, piegare e incollare, per ottenere le famose figure impossibili a tre e quattro travi inventate da Oscar Reutesvard.
L'artista svedese Oscar Reutesvard disegnò le prime costruzioni impossibili a tre e quattro travi nel 1934.
Nel 1958, Lionel Penrose e Roger Penrose ripresero l'idea nell'articolo Impossible objects: a special type of visual illusion, pubblicato sul British Journal of Psychology.
6 ottobre 2020 - 280.2020
Problemi capziosi
Sono quei problemi in cui la risposta giusta non è quella che si presenta alla mente per prima.
Per esempio:
Sto collezionando questi problemi nel Test di Bertoldino.
Se ne conoscete qualcuno, potreste proporlo nel Forum, per favore?
1 ottobre 2020 - 275.2020
Anagrammer, di Peter Pereira
If you believe in the magic of language,
then Elvis really Lives
...
If you believe the letters themselves
contain a power within them,
then you understand
what makes outside tedious,
how desperation becomes a rope ends it.
That eleven plus two is twelve plus one,
and an admirer is also married.
...
La forza di questa poesia sta negli anagrammi. Tradurla in italiano è un'impresa estrema che Franco Nasi è riuscito a compiere.
Memorabile, per esempio:
"how desperation becomes a rope ends it" che diventa
"e come il rimedio per la disperazione sia di penzolare".
E c'è anche un verso matematico:
"That eleven plus two is twelve plus one"
Quale potrebbe essere una valida traduzione in italiano?
---
La poesia originale e la traduzione di Franco Nasi si trovano qui: http://www.tecalibri.info/N/NASI-F_traduzioni.htm
26 settembre 2020 - 270.2020
Attraversare un fiume - variante UNESCO
L'UNESCO ha pubblicato nel 1988 un manuale intitolato Games and toys in the teaching of science and technology, a cura di Norman K. Lowe.
Un capitolo di questo manuale contiene una nuova versione del problema "Attraversare un fiume".
In questi problemi, forse per evitare qualunque forma di discriminazione, le persone sono identificate solo con numeri.
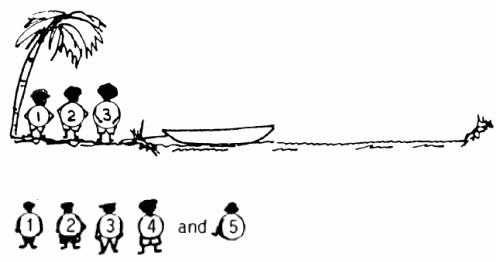
Uno dei 10 problemi proposti è il seguente.
Cinque persone numerate da 1 a 5 vogliono attraversare un fiume con una barca che può portare al massimo 2 persone.
Per di più due numeri consecutivi non possono attraversare assieme né rimanere mai da soli sulle rive del fiume.
Come si organizzano per l'attraversamento?
21 settembre 2020 - 265.2020
Numeri grandi
Ogni tanto scorro i libri della mia bibliotechina alla ricerca di qualche bel ricordo.
Oggi ho trovato il libro di Jorge Luis Borges, Cos'è il buddismo, con un segnalibro verde. Il segnalibro si trova sulla pagina che parla del kalpa.
Il kalpa è un intervallo di tempo lunghissimo. E' il tempo che passa tra la creazione e la dissoluzione dell'Universo. L'Universo si crea e si dissolve ciclicamente e ogni ciclo dura un kalpa.
Quanto dura un kalpa?
Si immagini una montagna di pietra che abbia 16 miglia di altezza. Ogni 100 anni la sfiora una sottilissima tela di Benares.
Quando quel lieve tocco abbia consumato la montagna, un kalpa non sarà ancora passato.
Poche pagine dopo, Borges parla della reincarnazione.
Quanto tempo passa prima che un essere, dopo la morte, si reincarni in un essere umano?
In una parabola si parla di una tartaruga che abita nel fondo del mare e ogni 100 anni sporge la testa alla superficie e di un anello che vi galleggia.
E' tanto improbabile che la tartaruga infili la testa nell'anello quanto che un essere, dopo la morte, si reincarni in un corpo umano.
Ogni quanto tempo, in media, un essere si reincarna in un corpo umano?
Forse questa domanda è più facile di quella sulla durata del kalpa.
21 settembre 2020 - 260.2020
Matematica rilassante con i sona drawings
Cari amici ho inserito un nuovo sfondo della home page usando alcuni disegni sona su 5 punti.
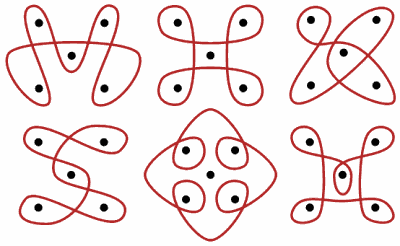
Ho un sacco di domande, per esempio:
11 settembre 2020 - 255.2020
Ex Falso sequitur quodlibet
In logica, usando correttamente le regole:
Ecco un esempio scherzoso che mostra come si possa dimostrare una proposizione Falsa partendo da una premessa Falsa.
F --> F
---
Uno studente chiese al famoso logico Bertrand Russell:
- E' vero che partendo da premesse false si può dimostrare qualunque cosa?
Russell rispose: - Certo!
- Sarebbe capace di dimostrare che se 2 + 2 = 5 allora lei è il Papa?
Bertrand Russell ci pensò un po' su poi disse:
Supponiamo che: 2 + 2 = 5;
sottraiamo 3 da entrambi i membri e otteniamo: 1 = 2;
quindi 1 = 2 e per simmetria 2 = 1.
Ora, io e il Papa siamo 2 persone ma siccome 2 = 1 allora io e il Papa siamo 1 persona.
Perciò io sono il Papa.
---
Ma come si può dimostrare il Vero partendo dal Falso?
F --> V
Per esempio, partendo dall'ipotesi 2 + 2 = 5, dimostrare 1 = 1.
6 settembre 2020 - 250.2020
Linea retta sul dodecaedro
Domanda: Esiste una linea retta disegnata sul dodecaedro regolare che parta da un vertice e arrivi allo stesso vertice senza passare attraverso nessun altro vertice?
Risposta: Sì, anzi ne esistono ben 31 famiglie!
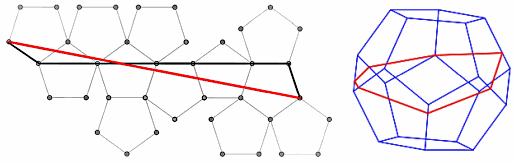
Domanda: Si può fare la stessa cosa sulla superficie degli altri 4 solidi regolari (tetraedro, cubo, etc)?
Risposta: No.
---
Spiegazione semplice del "Sì": A Trajectory from a Vertex to Itself on the Dodecahedron di Jayadev S. Athreya, David Aulicino, 2018. (https://arxiv.org/abs/1802.00811)
Spiegazione semplice del "Ne esistono 31 famiglie", su Quanta Magazine:
Mathematicians Report New Discovery About the
Dodecahedron di Erica Klarreich,
2020
(https://www.quantamagazine.org/mathematicians-report-new-discovery-about-the-dodecahedron-20200831/)
---
Il professor Howard Masur ha detto:
“It’s one of these things where I can say, without any hesitation, ‘Goodness, oh, I wish I had done that!’”
1 settembre 2020 - 245.2020
Buon anno scolastico a tutti!
Cari colleghi, genitori, studenti vi propongo un esercizio augurale per un buon anno scolastico 2020-2021.
E' un esercizio di ricerca e illuminazione, ispirato a La stella nascosta di Samuel Loyd.
---
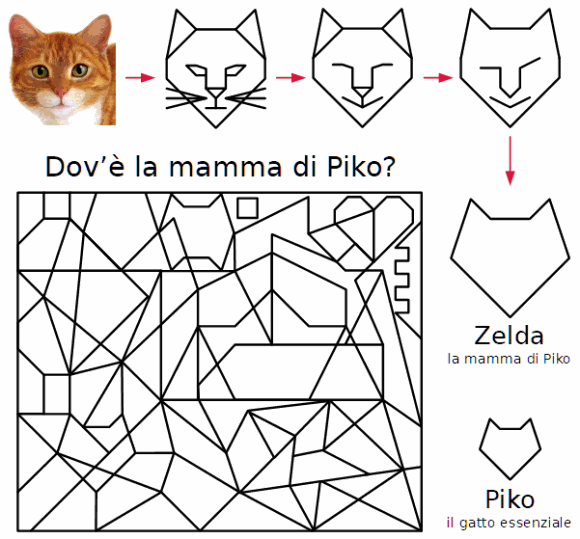
Dov’è la mamma di Piko?
Il gattino Piko si è infilato nella stanza dei giochi. C’è la stella di Sam
Loyd, ci sono due cuori, e poi il castello della paura e la corona della
regina.
Ma dov’è finito Piko? L’hai trovato? Bene.
Nella stanza c’è anche sua mamma Zelda.
Sei capace di trovarla?
27 agosto 2020 - 240.2020
Pensiero laterale matematico (2) [aggiornato]
Cari amici, vi propongo due problemi laterali che hanno qualcosa in comune, secondo me.
---
6. Attraversare un fiume
Due ragazzi devono attraversare un fiume, ma c'è una sola barca a remi che può trasportare un solo ragazzo alla volta.
La barca non può tornare indietro da sola.
Non ci sono corde o trucchi simili.
Nel fiume vivono pesci carnivori, perciò un ragazzo non può stare in acqua tenendosi alla barca.
Eppure entrambi i ragazzi riescono ad attraversare il fiume usando la barca.
Come si spiega?
---
5. Quanti triangoli?
Ho disegnato alcuni triangoli su un foglio di carta.
Per prima cosa ho mostrato il foglio a Mario e gli ho chiesto quanti triangoli c'erano. Mario ha detto 5 e aveva ragione.
Poi ho mostrato il foglio a Sofia e le ho chiesto quanti triangoli c'erano. Sofia ha detto 3 e aveva ragione.
Ripeto che le risposte date date da Mario e Sofia sono entrambe esatte.
Come si spiega? Quanti triangoli ci sono sul foglio?
Puoi illustrare la tua spiegazione con un disegno.
---
Cosa hanno in comune questi due problemi?
---
Tratti dal blog di Tanya Kovanova
22 agosto 2020 - 235.2020
Certi problemi, che io chiamo "tigri di carta", sembrano difficili da domare ma basta una piccola astuzia per smascherare la loro semplicità.
Però può capitare che dietro la tigre di carta si nasconda la criniera di un leone in carne ed ossa.
Per esempio...
Numeri quadrati perfetti che contengono solo due cifre distinte
Versione facile.
Immagina un numero di duecento cifre formato da cento "2" e cento "4".
Dimostra che, in qualunque modo siano disposte le cifre, tale numero non sarà mai un quadrato perfetto.
Questo problema si può risolvere a mente con le nozioni matematiche che si imparano in prima media.
Versione difficile.
6661661161 = 816192
Il numero 6661661161 è il più grande numero conosciuto che sia un quadrato, contenga soltanto due cifre distinte e non termini per 0.
Trova un numero più grande che abbia le stesse caratteristiche oppure dimostra che non esiste.
Questo è un problema non ancora risolto.
Vedi la sequenza A018884 - Squares using at most two distinct digits, not ending in 0 su OEIS.
17 agosto 2020 - 230.2020
Zero e uno in cerchio
Scrivete quattro 1 e cinque 0 in cerchio, in ordine casuale.
Poi applicate la seguente regola:
Potete applicare nuovamente la regola, quante volte volete.
Per esempio nella figura, a sinistra, vedete una possibile distribuzione iniziale di 1 e 0. A destra, invece, ciò che si ottiene applicando la regola una volta.
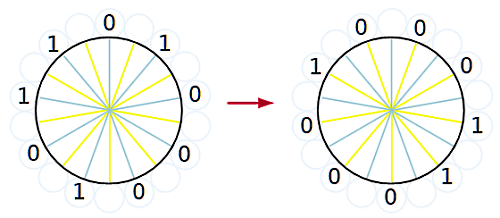
Domanda: è possibile ottenere tutti 1 applicando la regola un numero finito di volte?
Suggerimento: è un problema che si può risolvere partendo dal fondo e procedendo a ritroso.
Ho aggiornato la pagina Quando si comincia dal fondo.
---
Tratto da: Strategies of problem solving (Draft) di Maria Nogin, 2008.
Questo problema è citato anche nel libro The Mathematics of Various Entertaining Subjects, Volume 3 - The Magic of Mathematics, a cura di Jennifer Beineke e Jason Rosenhouse, 2019.
12 agosto 2020 - 225.2020
Umorismo matematico 19-20 [aggiornato]
20. A lezione da Schrodinger
7 agosto 2020 - 220.2020
I disegni del popolo Chokwe
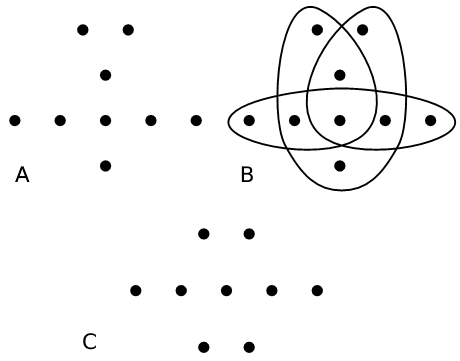
Provate a risolvere il problema con la struttura di punti mostrata nella figura C.
---
Questo è un esempio di etnomatematica, studiato recentemente da David Eppstein e altri nell'articolo New Results in Sona Drawing: Hardness and TSP Separation (https://arxiv.org/abs/2007.15784).
Altri esempi di etnomatematica si trovano nel libro di Claudia Zaslavsky, Multicultural Mathematics, 1993.
2 agosto 2020 - 215.2020
Posso dire che 1 è un numero primo?
Breve storia della primalità di 1.
Immaginiamo di chiedere ai grandi matematici della storia:
"Si può dire che 1 è un numero primo?"
Le risposte sarebbero...
28 luglio 2020 - 210.2020
Ho aggiornato la pagina Spazio, tempo, velocità con un nuovo problema.
Emma e Greta vanno al parco
Emma e Greta sono sorelle gemelle che hanno la stessa velocità di camminata e la stessa velocità di corsa.
Un giorno fanno un viaggio al parco.
Emma cammina per metà della distanza e corre per l'altra metà.
Greta cammina per metà del tempo e corre per l'altra metà del tempo.
Chi arriva al parco per prima?
---
Tratto da AoPS online (https://artofproblemsolving.com/online)
23 luglio 2020 - 205.2020
Una sequenza per futuri veterinari
Cari amici, questa è una fedele riproduzione di un quesito tratto da qui.
---
---
Ho inserito questo quesito nella pagina: Posso dire che 1 è un numero primo?
18 luglio 2020 - 200.2020
Il numero cromatico del piano
Comincio questo appunto col teorema di Adamo, Eva e Bertoldino.
Immaginate di avere un foglio grande come il piano geometrico e 1, 2, 3, 4, ...n colori.
Per esempio, scelti i 2 colori rosso e blu, il piano è 2-colorato quando ogni suo punto è rosso oppure blu.
La colorazione può avvenire in infiniti modi, senza alcuna restrizione sulla distribuzione dei colori.
---
Teorema. In qualunque modo sia 2-colorato il piano e qualunque unità di misura si scelga, esistono almeno due punti dello stesso colore che distano fra loro 1 unità.
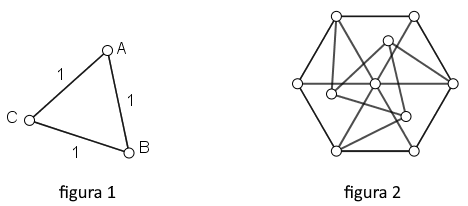
Per dimostrarlo basta lanciare nel piano un triangolo equilatero di lato 1 (fig.1).
Se invece lanciate un grafo di Golomb (fig. 2) potete dimostrare che anche in un piano 3-colorato esistono almeno due punti dello stesso colore che distano fra loro 1 unità.
15 luglio 2020 - 197.2020
Buon compleanno BASE Cinque!
Oggi sono felicemente commosso: BASE Cinque compie 20 anni!
Penso con gratitudine a tutti gli amici che hanno contribuito al sito dapprima con e-mail, poi partecipando al forum su VoyForum e attualmente al forum gestito da Pietro Vitelli. Grazie di cuore a tutti!
Il mio piccolo regalo al sito è un problema del grande maestro Nobuyuki Yoshigahara pubblicato sul suo libro Puzzles 101: A PuzzleMasters Challenge, CRC Press, 2004.
---
Una calcolatrice rotta.
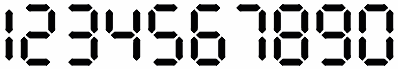
La mia calcolatrice è rotta: non mostra più sul display i segmenti
verticali delle cifre.
Ho digitato un numero da una cifra e il display mostra tre segmenti
orizzontali.
Quale operazione potresti fare per scoprire il numero che ho digitato?
8 luglio 2020 - 190.2020
Astronave intergalattica
A volte nel Forum partiamo da un problema preciso, lo risolviamo con onore e poi divaghiamo un po'. Il filo del discorso è matematico ma è fatto di associazioni fantasiose e talvolta di bei ricordi.
La discussione "I sei quadrati", per esempio, è partita da un problema sull'area di un triangolo per arrivare all'ellisse, poi a un'astronave intergalattica e infine al concetto urbanistico di città equa.
Come ha detto Pasquale: "Tanto mi piacque questa discussione!"
Bruno ci ha persino donato il disegno dell'astronave.
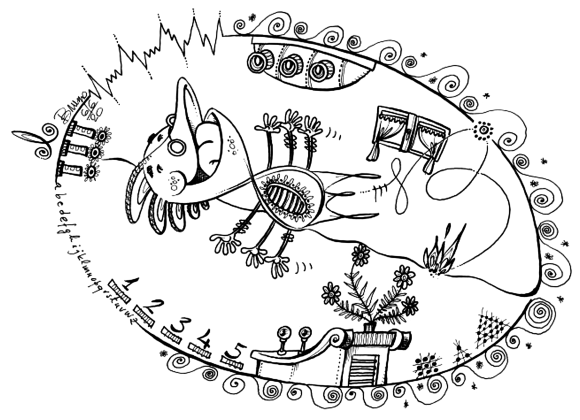
Quanti aspetti matematici riuscite a trovare nel disegno?
Grazie a Bruno, Panurgo, Pasquale, Lucignolo e Delfo52 per i loro contributi.
3 luglio 2020 - 185.2020
Il problema dei cinque ponti
L'immagine mostra cinque ponti che collegano le rive opposte di un fiume passando attraverso due isole. Ci sono diversi modi per attraversare il fiume usando alcuni ponti.
Ieri c'è stata una tempesta così forte che ciascun ponte ha avuto il 50% di probabilità di crollare. Oggi, Aldo arriva al fiume e deve attraversarlo.
Data la disposizione dei ponti e delle isole, qual è la probabilità che Aldo sia in grado attraversare il fiume?
---
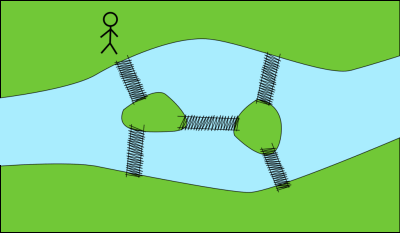
E' un problema semplice ma interessante perché ci fa riflettere, tra
l'altro, sull'importanza della simmetria in matematica.
Se volete commentare o proporre una soluzione, trovate questo problema anche
nel Forum.
Tratto da: The five bridges puzzle di Katie Steckles, (https://scilogs.spektrum.de/hlf/the-five-bridges-puzzle/)
28 giugno 2020 - 180.2020
Un teorema quasi straordinario in una data quasi perfetta
Il 28/6/496 fu una data perfetta. In quell'anno l'Italia era governata da Teodorico, re degli Ostrogoti.
Il 28/6/8128, sarà la prossima data perfetta. Chissà come sarà il mondo...
Oggi, 28/6/2020 è una data quasi perfetta e vi propongo un teorema quasi straordinario.
Tutto nasce dalla domanda:
È possibile dividere l’insieme dei numeri naturali in due parti in modo che nessuna delle due contenga una terna pitagorica?
E' una domanda che ci fa immergere nell'infinito. Se la risposta fosse "sì", la dimostrazione sarebbe davvero straordinaria.
Ma la risposta è "no" e deriva dal seguente teorema:
Teorema. L'insieme {1, 2, 3, ..., 7824} si può dividere in due parti tali che nessuna delle due contenga una terna pitagorica. Tale divisione è invece impossibile con l'insieme {1, 2, 3, ..., 7825}.
La dimostrazione ha richiesto circa 35.000 ore di calcolo ma siccome è stata realizzata da una "nuvola" di 800 computer che hanno lavorato in parallelo, si è conclusa in soli 2 giorni.
Il "testo" non compresso della dimostrazione occupa circa 200 terabyte.
Vorrei fare un confronto con l'Ulysses di James Joyce. La versione che si trova sul Progetto Gutenberg è formata da 1.481.456 caratteri (spazi compresi). Ogni carattere occupa 1 byte di memoria.
Poiché 1 terabyte = 1012 = 1.000.000.000.000 byte, possiamo concludere che la dimostrazione è lunga circa 135 milioni di volte l'Ulysses di Joyce.
Nessuno di noi può verificarla e neppure scaricarla con il proprio computer personale.
Possiamo accettarla come dimostrazione?
Il racconto di come è stata ottenuta si trova su arXiv.org (https://arxiv.org/abs/1605.00723)
Marijn J. H. Heule, Oliver Kullmann, Victor W. Marek, Solving and Verifying the boolean Pythagorean Triples problem via Cube-and-Conquer.
23 giugno 2020 - 175.2020
Divertitevi con questo classico. Potete anche fare una mini-installazione in grandezza naturale.
18 giugno 2020 - 170.2020
Il problema delle quattro R [aggiornato]
Ho aggiornato questo problema con i contributi di Pietro Vitelli e di Sergio Casiraghi.
Finalmente questo problema è (abbastanza) risolto!
13 giugno 2020 - 165.2020
Se A fosse B, cosa sarebbe C?
[aggiornato]
Cinque per 6 uguale trentasei
Sappiamo che:
5·6 fa 6²
59·60 fa 82²
858·859 fa 1624².
Quanto fa 100?
---
Grazie a Bruno per il problema!
8 giugno 2020 - 160.2020
Due problemi aritmetici dal Forum
Per risolvere quest'ultimo problema bisogna chiarire come si calcola
un'espressione del tipo:
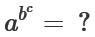
Infatti l'operazione di elevamento a potenza non è associativa.
Per
convenzione, in assenza di parentesi, si usa l'associatività
a destra, cioè:
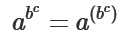
Per esempio:
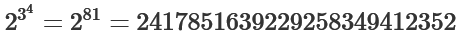
Maxima,
Sage, WolframAlpha seguono questa convenzione.
Invece Maple, Calc, Excel e alcune calcolatrici, in
assenza di
parentesi, associano a sinistra:
,
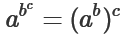per esempio:
---
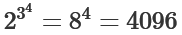
Grazie a Pietro e Bruno per i problemi!
3 giugno 2020 - 155.2020
Il tangram ovale - compito per le vacanze [aggiornato]
Cari amici, vi propongo un compitino per le vacanze.
Con un cartoncino colorato costruite il tangram ovale che si vede qui sotto. Il taglio lungo la linea tratteggiata arancione è facoltativo (ma utile). Usatelo per costruire le figure più disparate: uccelli e altri animali, persone, astronavi, figure astratte e così via.
Per sapere come si disegna il tangram ovale potete dare un'occhiata sulla pagina Il tangram ovale.
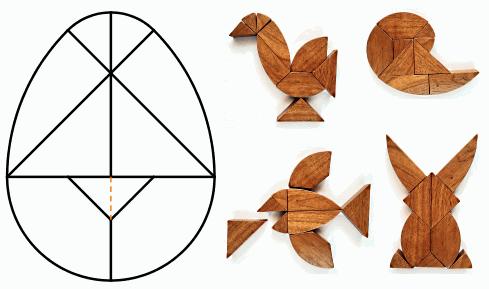
Se volete, inviatemi una foto di ciascuna vostra costruzione, sarà graditissima!
Buona conclusione dell'anno scolastico e buone vacanze a tutti!
---
Grazie a Dario Uri per le preziose notizie storiche su questo gioco, inviate tramite Facebook.
29 maggio 2020 - 150.2020
Due simpatiche risposte al Test di Bertoldino
---
Grazie a Emma Taglier, Federico e Paolo Vecchio e alla loro insegnante Paola Maria Coppo!
Beh, la morale è che bisogna formulare i testi dei problemi con molta cura. Ho apportato qualche correzione al Test.
24 maggio 2020 - 145.2020
Il compleanno di Cheryl
Albert e Bernard sono diventati amici di Cheryl, e vogliono conoscere la data del suo compleanno. Cheryl dà loro 10 possibili date:
Poi Cheryl dice separatamente ad Albert solo il mese e a Bernard solo il giorno del proprio compleanno.
Tra i due amici segue questo dialogo:
Dunque, quando è il compleanno di Cheryl?
---
Note.
Questo problema è stato ideato da Joseph B. W. Yeo e proposto nel 2015 alle Olimpiadi di Matematica di Singapore (SASMO), scuola secondaria.
Per un certo periodo è diventato virale nei social tipo FB. E' stato pubblicato persino su la Repubblica e The Guardian!
Potrebbe essere definito un problema di conoscenza e ignoranza, come il famoso problema impossibile di H. Freudenthal (1969) e D. Sprows (1976).
Merita un approfondimento.
Grazie a Lucignolo per aver proposto il problema nel Forum.
19 maggio 2020 - 140.2020
Il principio della cassettiera [aggiornato]
Cari amici ho aggiornato la pagina con la risoluzione del problema 24.
E' tratto dal libro Introductory Graph Theory di Gary Chartrand, 1985 (prima edizione del 1977 col titolo Graphs as Mathematical Models).
Gary Theodore Chartrand (n. 1936) ha numero di Erdos 1.
---
Grazie a Pietro Vitelli e Giobimbo per la soluzione del problema nel Forum.
14 maggio 2020 - 135.2020
Il trucco con le carte più semplice del mondo
Preparate un mazzo formato da 20 carte da gioco con i semi di due colori diversi: 10 rosse e 10 nere.
I dorsi delle carte devono essere tutti uguali, indistinguibili l'uno dall'altro.
Chiedete a un amico/a di mescolare le carte e di consegnarvi il mazzo dalla parte del dorso.
A questo punto inizia il trucco. Dovrete usare la vista a raggi X.
Tenendo le carte sempre rivolte dalla parte del dorso, dividetele in due mazzetti da 10 carte posandole sul tavolo una alla volta, a destra oppure a sinistra a vostro piacere.
Terminata la divisione dichiarate: "Le carte rosse del mazzetto di destra sono tante quante le carte nere del mazzetto di sinistra!"
Chiedete all'amico/a di verificare. Sarà proprio così!
Come avete fatto?
Questo trucco può aiutare a risolvere un noto problema sul travaso di latte e caffè. Quale?
9 maggio 2020 - 130.2020
Pensiero laterale matematico (2) [aggiornato]
Sui social network, come FB, si trovano molti esercizi come questi. Che ne dite di risolverli?
Attenti a non scivolare sulla buccia di banana!
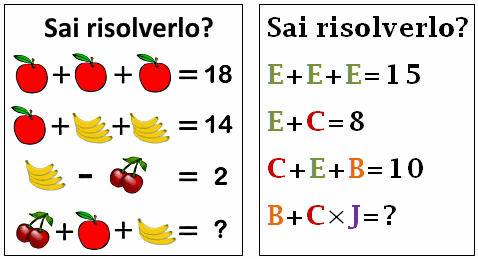
Visitare tutte le celle di una griglia [aggiornato]
Grazie a Giobimbo per la soluzione di un problema di Dudeney.
Il problema delle quattro R [aggiornato]
Grazie a Pietro Vitelli per le nuove soluzioni.
4 maggio 2020 - 125.2020
Umorismo matematico 19-20 [aggiornato]
Credit: CommitStrip
29 aprile 2020 - 120.2020
Il problema del collezionista (coupon collector's problem)
24 aprile 2020 - 115.2020
Alcool 70% vol
La nonna vuole sapere quanti millimetri di acqua deve aggiungere nella bottiglia per ottenere una soluzione con gradazione alcolica 70% vol.
Cioè la soluzione dovrebbe essere formata dal 70% di alcool e dal 30% di acqua, in volume.
Il liquido già presente nella bottiglia è una soluzione alcolica al 96% vol.
La nonna si accontenta di un valore approssimato che non tenga conto delle forze tra le molecole dell'alcool e quelle dell'acqua...
---
Note.
19 aprile 2020 - 110.2020
Un'altra idea di John Horton Conway che mi piace ricordare.
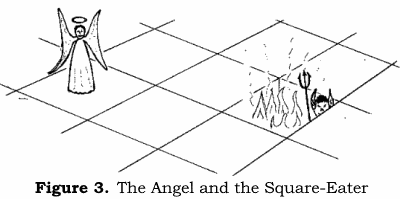
Questo gioco ideale si svolge su una scacchiera infinita formata da caselle dello stesso colore, con due pedine: l'Angelo contro il Diavolo.
---
Figura tratta da: Berlekamp, Conway, Guy, Winning Ways for Your Mathematical Plays, 2003.
14 aprile 2020 -
105.2020
La subdola discriminazione dei matematici ebrei russi in Unione Sovietica negli anni '70 e '80. Una storia con lieto fine, a volte.
Anno 1984. Ufficio di iscrizione all'Università statale di Mosca (MGU), Dipartimento di Meccanica e Matematica, (Mekh-Mat). Per essere ammessi al Mekh-Mat bisogna superare un esame scritto e uno orale ottenendo il massimo punteggio, cioè 5 punti.
Il candidato è Edward Vladimirovich Frenkel, 16 anni.
Impiegata: "Buongiorno. Come si chiama?"
Studente: "Eduard Frenkel."
"E vuole fare domanda di iscrizione alla MGU?"
"Sì."
"Quale dipartimento?"
"Mekh-Mat."
"Bene."
L'impiegata abbassò gli occhi e chiese:
"Qual è la sua nazionalità?"
"Russa."
"Davvero? E quali sono le nazionalità dei suoi genitori?"
...
E' una mia libera ricostruzione tratta dal libro: Edward Frenkel, Love and Math: The Heart of Hidden Reality, Basic Books, New York, 2013.
13 aprile 2020 -
104.2020
Su BASE Cinque ci sono molte pagine che parlano di John Horton Conway.
Qui mi piace ricordare:
Il teorema cosmologico (javascript)
Il gioco Life (Vita) (javascript)
John Horton Conway ci ha lasciato l'11 aprile 2020 all'età di 82 anni a causa del COVID-19. Si trovava a Princeton (New Jersey).
9 aprile 2020 -
100.2020
Bilance a due piatti [aggiornamento]
Bilance con scala graduata [aggiornamento]
Ho riorganizzato i problemi di pesata in due pagine: bilance a due piatti o a leva e bilance con scala graduata.
4 aprile 2020 -
95.2020
Bilance con scala graduata [aggiornamento]
Ho aggiornato la pagina con un nuovo problema.
1100 grammi di farina
Hai alcuni sacchi di farina da 2 chili e mezzo; una bilancia a due piatti, e un peso da 100 grammi.
Devi fare un sacchetto da 1100 grammi di farina.
Come fai?
Qual è il numero minimo di pesate?
---
Grazie a Delfo52 per aver inviato questo problema al Forum - Ennesimo quiz di pesate. Il problema è tratto dal blog di Maurizio Codogno.
30 marzo 2020 -
90.2020
Storia, varianti e soluzioni di un racconto matematico.
25 marzo 2020 -
85.2020
La Biblioteca di BASE
Cinque [nuovo aggiornamento]
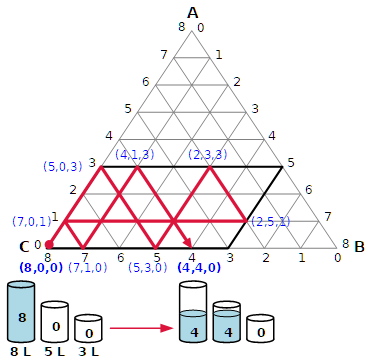
In questi giorni mi sono finalmente deciso a ricostruire la storia del problema delle tre brocche.
La difficoltà principale è stata quella di trovare in rete gli Annales Stadenses dell'abate Alberto di Stade (1187-1260), scritti in latino, nei quali si trova la versione più antica di questo problema.
Alla fine li ho trovati ed è stata un bella emozione. Gli Annales Stadenses sono una cronaca universale dalla Creazione del mondo al 1256. La sorpresa è che a un certo punto c'è un dialogo tra due giovani litterati, curiales et curiosi di nome Tirri e Firri i quali si lanciano sfide matematiche. Il dialogo si svolge la vigilia di Natale del 1179, anno in cui morì Santa Ildegarda di Bingen.
dMGH - digitalen Monumenta Germaniae Historica
Contiene gli Annales Stadenses in cui si trova la prima versione del problema delle tre brocche. Link diretto: Annales Stadenses.
20 marzo 2020 -
80.2020
La Biblioteca di BASE
Cinque [aggiornato]
Ho aggiunto due nuovi link e aggiornato la pagina.
BHL - Biodiversity Heritage Library
Si propone di fornire l'accesso gratuito alla conoscenza collettiva mondiale sulla biodiversità: libri, riviste, immagini.
Ci sono anche molti documenti di matematica in italiano, come le "Memorie di matematica e di fisica della Società italiana delle Scienze".
E' uno spazio virtuale per collezionisti di libri rari e appassionati di storia per leggere, discutere, riscoprire e scaricare gratuitamente libri perduti.
Vi si trova A synopsis of elementary results in pure and applied mathematics, di George Shoobridge Carr, London, 1880, uno dei testi più amati da Ramanujan.
13 marzo 2020 -
73.2020
La prima Giornata Internazionale della Matematica
Cari amici, il 14 marzo 2020 è la prima Giornata Internazionale della Matematica e anche un Pi-day.
Ecco il mio problemino per festeggiare.
---
Nella figura vedete le prime 250 cifre di pi greco (senza la virgola decimale).
In rosso sono evidenziate le prime volte in cui compaiono coppie di cifre uguali.
Per esempio, la coppia 33 compare per la prima volta alla posizione 25-26 mentre la coppia 22 compare alla posizione 136-137.
a) In quale posizione compaiono per la prima volta le coppie 00 e 77?
b) E le terne 000 e 777?
10 marzo 2020 -
70.2020
Domanda 1a.
Considerate i numeri da 1 a 6. Riuscite a disporli nelle seguenti caselle
rispettando i segni di ordinamento scritti fra di loro?
Domanda 1b.
Che ne dite di sistemare i numeri da 1 a 9 nelle seguenti caselle?
Domanda 2.
Generalizziamo.
Dato un elenco di n numeri (tutti distinti tra di
loro) e una serie di n caselle con segni di
ordinamento inseriti fra loro, inventate un algoritmo che metta i numeri nelle
caselle rispettando i segni.
Limitiamoci a carta e penna.
---
Grazie a Bruno per aver inviato questo problema al Forum - Indovinello algoritmico.
5 marzo 2020 -
65.2020
Il problema dei lucchetti ovvero amore in Kleptopia [aggiornato]
Aldo e Beatrice si sono innamorati (via Internet) e Aldo desidera inviarle un anello molto prezioso.
Sfortunatamente vivono nel Paese di Kleptopia dove qualsiasi cosa inviata per posta sarà rubata a meno che non sia racchiusa in una scatola con un lucchetto. Aldo e Beatrice hanno ciascuno un lucchetto con la relativa chiave, ma nessuno dei due ha la chiave del lucchetto posseduto dall'altro.
a) Come può fare Aldo per inviare l'anello a Beatrice in modo che non sia rubato?
b) Come può l'astuta kleptomaniaca Eva rubare l'anello?
c) Come funziona lo scambio di chiavi Diffie-Hellman?
---
Si trova nell'articolo di Peter Winkler, Seven Puzzles You Think You Must Not Have Heard Correctly, 2006. L'autrice del problema è Caroline Calderbank, figlia dei matematici Ingrid Daubechies e Rob Calderbank.
29 febbraio 2020 -
60.2020
Umorismo matematico 19-20 [aggiornato]
18. Raccolta di battute
E molte altre...
Tratte dal blog di Tanya Khovanova.
24 febbraio 2020 -
55.2020
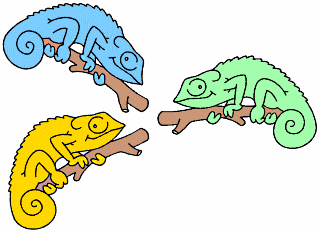
In un'isola vivono 2 camaleonti blu, 5 gialli e 3 verdi.
Se due camaleonti di due colori diversi si incontrano, cambiano entrambi colore e diventano del terzo colore.
Per esempio, se si incontrano un camaleonte verde e uno giallo diventano entrambi blu.
a) Descrivete la più breve sequenza di incontri in cui tutti i camaleonti diventano verdi.
b) Dimostrate che i camaleonti dell'isola, in queste circostanze, non potranno mai diventare tutti gialli.
---
Questo problema è apparso per la prima volta (?) nel 1984, nell'International Mathematics Tournament of the Towns, Russia (con i numeri 13, 15, 17), ideato da V. G. Ilichev.
Si trova anche nel libro di Terence Tao, Solving Mathematical Problems. A Personal Perspective, Oxford University press, 2006.
Ci sono altre varianti con i numeri (20, 18, 16) e (12, 15, 18).
19 febbraio 2020 -
50.2020
Una sequenza di Nob Yoshigahara
I numeri nei cerchi bianchi sono scritti seguendo una certa regola.
a) Scoprite la regola e scrivete il valore di x.
b) Meditate sulla psico-logica con cui è stato scritto questo gioco e scrivete i valori di y e z.
c) Potete pure scrivere un programma per trovare i numeri y e z.
---
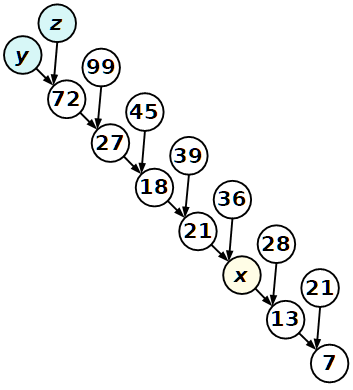
E' l'espansione di un problema di Nobuyuki Yoshigahara pubblicato sul suo libro Puzzles 101: A PuzzleMasters Challenge, CRC Press, 2004 .
14 febbraio 2020 -
45.2020
Le radici quadrate di un numero complesso: la via semplice
Quali sono le radici quadrate di 5+12i?
9 febbraio 2020 -
40.2020
Linguaggio BASIC
In questi giorni ho scoperto che suor Mary Kenneth Keller B.V.M. (1913-1985) negli anni '60 collaborò con John Kemeny e Thomas Kurtz alla creazione del linguaggio BASIC.
Suor Mary Kenneth Keller (fonte: Catholic Archives)
Il BASIC è sempre stato il mio linguaggio preferito per fare indagini in matematica.
D'ora in avanti lo sarà ancora di più!
Attualmente uso il Decimal Basic di Shiraishi Kazuo. E' un progetto libero e open source.
2 febbraio 2020 -
33.2020
Una data curiosa [dal Forum]
Ronfo ci segnala dal Forum che oggi, 02022020, è una data palindroma, cioè ha lo stesso valore letta da sinistra oppure da destra, anche con la notazione inglese (mmggaaaa)
Inoltre è il 33-esimo giorno dell'anno e mancano 333 giorni al termine dell'anno stesso.
Delfo52 aggiunge che 02022020, se scritto nella notazione a 7 segmenti, è un numero metazetico cioè rimane lo stesso se la scritta viene ruotata di 180°.
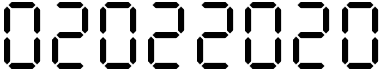
Quanti sono i numeri metazetici composti da n cifre scritte con la notazione a 7 segmenti?
29 gennaio 2020
Umorismo matematico 19-20 [aggiornato]
16. La tavola pitagorica dei sentimenti.
Compresi quelli dei prof. di matematica nell'esercizio delle loro funzioni.
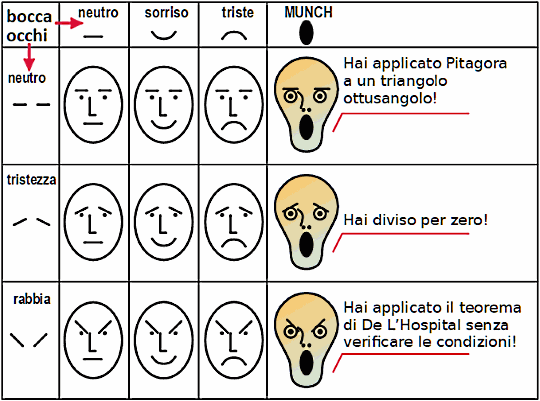
Inventate una frase di matematica per ogni faccina.
Se la frase non è di matematica, va bene lo stesso.
24 gennaio 2020
La pagina aperta del 153 [aggiornato]
In questi giorni, leggendo il Discorso sulla preghiera di Nilo Asceta (440 d.C.), ho incontrato di nuovo il numero 153. L'autore spiega che il suo Discorso è diviso in 153 capitoli in ricordo della pesca miracolosa di 153 grossi pesci di cui si parla nel Vangelo di Giovanni, 21, 11.
Poi aggiunge alcune spiegazioni matematiche sul significato simbolico di questo numero. Ma non cita la nota proprietà che riguarda la somma dei cubi delle sue cifre.
Chi ha scoperto per primo questa proprietà?
Sembra che sia stato un certo Phil Kohn di Yokneam, Israele.
Ecco la citazione originale di T. H. O'Beirne, sulla rivista New Scientist del 1961.
---
Tratto da: T. H. O'Beirne, Christmas puzzles, New Scientist n. 266, 21 dicembre 1961.
Il mistero rimane, anche perché non sono riuscito a trovare altre notizie né su O'Bernie né su Phil Kohn.
So solo che T. H. O'Beirne scrisse il libro Puzzles and Paradoxes, 1965, Oxford University Press, nel quale raccolse alcuni suoi articoli pubblicati su New Scientist dal gennaio 1961 al febbraio 1962.
Qualunque aiuto è benvenuto!
19 gennaio 2020
Umorismo matematico 19-20 [aggiornato]
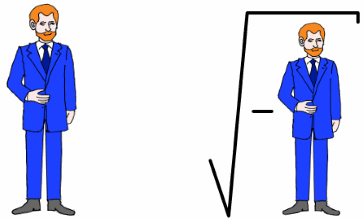
15. Il principe immaginario di Hans Christian Kronecker
C'era una volta un ℝeale chiamato "principe Harry" che voleva cambiare segno e andare a vivere sotto una radice quadrata...
14 gennaio 2020
Terence Tao ha quasi-dimostrato la Congettura di Collatz
Il problema di Collatz lo può capire anche un bambino che sappia calcolare il triplo e la metà di un numero.
Tuttavia nessun matematico, negli ultimi 90 anni, è ancora riuscito a dimostrare che alla fine si raggiunge sempre il numero 1.
La congettura di Collatz ovvero il problema 3x+1 Scegli un numero intero x e applica la seguente operazione, che si chiama funzione C:
Il risultato è un nuovo numero, C(x). Ripeti l’operazione sul nuovo numero, ottenendo C(C(x)) e così via. Qualunque sia il numero x di partenza, continuando a ripetere l’operazione, arriverai sempre a ottenere il numero 1 dopo un numero finito di passi. Se continui, finirai intrappolato in un ciclo senza fine: 4, 2, 1, 4, 2, 1, ... |
Il mitico Terence Tao ha dimostrato nel settembre 2019 che:
"ALMOST ALL ORBITS OF THE COLLATZ MAP ATTAIN ALMOST BOUNDED VALUES"
Si potrebbe tradurre così:
"Quasi tutte le traiettorie del grafo di Collatz raggiungono valori quasi limitati."
E' interessante capire cosa intendono i matematici quando parlano di "quasi tutti" gli elementi di un insieme infinito.
E anche cos'è una quasi-dimostrazione.
Per chi vuole approfondire, c'è l'articolo di Tao su ArXiv:
https://arxiv.org/abs/1909.03562
7 gennaio 2020
L'area del corpo umano
Ieri stavo esplorando un sentiero di confine tra la Geometria solida e quella piana quando improvvisamente un Troll è uscito da un albero e mi ha chiesto:
"Conosci una formula per calcolare l'area della tua pelle?"
Ho fatto un po' di ricerca e ho scoperto che esistono diverse formule empiriche per stimare l'area del corpo umano. E che c'è un modo molto carino per trovarle.
La formula di R. D. Mosteller è quella più semplice:
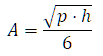
dove h è la statura è espressa in metri e il p è peso corporeo in chilogrammi.
Il risultato ci dà la superficie della pelle in metri quadrati.
Una spiegazione interessante si trova in questo articolo:
Lee, Joo Young & Choi, Jeong-Wha & Kim, Ho. (2008). Determination of Body Surface Area and Formulas to Estimate Body Surface Area Using the Alginate Method. Journal of physiological anthropology. 27. 71-82. 10.2114/jpa2.27.71.
P.S. Gli alginati si usano anche in cosmetica.
1 gennaio 2020
Buon 2020!
Auguro a tutti pace, bene e un percorso con le difficoltà della vita putroppo inevitabili ma che siano tutte superabili.
Utile il riepilogo finale, prima di passare all'anno successivo.
Un po' come in questo labirinto che vi propongo di risolvere mentalmente.
Mi dicono che il 2020 è un numero autobiografico.
Perché è formato da 2 "zeri", 0 "uno", 2 "due" e 0 "tre".
Ma la definizione ufficiale di numero che è la biografia di se stesso (autobiographical number) mi lascia un po' perplesso: infatti, prima di definire il concetto di auto-biografia si dovrebbe definire cos'è la biografia di un numero.
Il diario di BASE Cinque - 2019
Il diario di BASE Cinque - 2018
Negli anni 2016 e 2017 BASE Cinque è stato in power-saving mode.
Il diario di BASE Cinque - 2015
Il diario di BASE Cinque - 2014
Il diario di BASE Cinque - 2013
Il diario di BASE Cinque - 2012
Il diario di BASE Cinque - 2011
Il diario di BASE Cinque - 2010
Il diario di BASE Cinque - 2009
Il diario di BASE Cinque - 2008
Il diario di BASE Cinque - 2007
Degli anni 2005 e 2006 non esiste il diario.
Ricreazioni ricevute 2000 - 2004
Il sito BASE Cinque è nato il 15 luglio 2000.
BASE Cinque - Appunti di Matematica ricreativa (2000-2020)
Sito Web realizzato da Gianfranco Bo
Forum amministrato da Pietro Vitelli - Logo di B5 creato da Bruno Berselli
