24 dicembre 2013 - NOTTURNO[BASE Cinque - Appunti di Matematica ricreativa]
24 dicembre 2013 - NOTTURNO
Dal Notturno vi propongo una scelta di irresistibili di Natale.
Stillenacht 1 (classica) - Stillenacht 2 (classica) - Stillenacht 3 (fantasia piano) - Stillenacht 4 (pastorale) - Stillenacht 5 (jazz) - Stillenacht 6 (piano jazz) - Jingle Bells 1 (jazz) - Jingle Bells 2 (violini) - Jingle Bells 3 (banjo) - Jingle Bells 4 (stride piano) - Alleluia (gospel orchestra) - Adeste fideles (orchestra) - Ave Maria (orchestra) - Bianco Natale 1 (stride piano) - Bianco Natale 2 (orchestra) - Bianco Natale 3 (swing) - Bianco Natale 4 (orchestra) - Bianco Natale 5 (piano) - Gloria (orchestra) - Greensleeves (percussioni) - Happy Christmas (John Lennon) - Happy Christmas2 (John Lennon) - Oh Tannenbaum (originale) - Oh Tannenbaum (piano jazz) - Tu scendi dalle stelle (classica) - We shall overcome (piano) - Oh happy day (orchestra, Edwin Hawkins) - When the saints go marching in (banjo) - Jingle bell rock (orchestra).
15 dicembre 2013 - SEGNALAZIONI
Credit: Rai.tv. Giorgio Dendi alla trasmissione "Superbrain" del 14/12/2013.
Immaginavo che, nella sua prova, avrebbero aggiunto dei distrattori, ma avevo in mente che sarebbero state introdotte musica e ballerine spettacolari, invece… il nostro eroe è stato legato a una grande ruota girevole sulla quale i numeri erano scelti a caso da un lanciatore di coltelli. Giorgio è stato messo sotto un vero e proprio stress fisico ed emotivo, per creargli difficoltà nella sua capacità di concentrazione e di calcolo. Bravissimo Giorgio, per essere riuscito a mantenere, comunque, la simpatia, il sorriso e la necessaria concentrazione! E naturalmente per aver superato la prova!
Credit: Ivana Niccolai, dal Forum di BASE Cinque.
Credit: Rai.tv. Giorgio Dendi calcola in pochi secondi la radice 9° di quel numero gigantesco che vedete nella foto, alla trasmissione "Superbrain" del 14/12/2013. Credit: Rai.tv.
Per chi non avesse potuto seguire il programma, segnalo, al seguente link, il video relativo: Superbrain 14-12-2013.
13 dicembre 2013 - SEGNALAZIONI
Sabato 14 dicembre su Rai 1 alle ore 21.10, Giorgio Dendi parteciperà a "Superbrain - le supermenti", condotto da Paola Perego.
Come prima prova, Giorgio cercherà di calcolare a mente delle radici, non solo quadrate, ma molto peggio, partendo da numeri che hanno fra le 10 e le 20 cifre.
Se andrà in finale, come seconda prova, calcolerà a mente... non lo diciamo, per scaramanzia...
In studio sarà presente il neurochirurgo Marcello Marchetti che spiegherà come il cervello umano può riuscire fare operazioni strabilianti anche in condizioni di stress.
Un appuntamento da non perdere!
Giorgio Dendi alla trasmissione "Scommettiamo che..." (anni 90).
12 dicembre 2013 - SEGNALAZIONI
Emma Castelnuovo è nota a tutti gli insegnanti di matematica per i suoi importanti contributi alla didattica della geometria.
Oggi Emma Castelnuovo compie cento anni!
L'augurio animato è di Ivana Niccolai (con una piccola modifica).
Dalla prefazione del libro di Emma Castelnuovo, La geometria intuitiva del 1948: "È necessario animare la naturale e istintiva curiosità che hanno i ragazzi, dagli undici ai quattordici anni, accompagnandoli nella scoperta delle verità matematiche, trasmettendo l’idea di averlo fatto per se stessi."
Nel blog Pintadera potete leggere una bellissima poesia di Grazia Raffa dedicata a Emma Castelnuovo.
6 dicembre 2013 - LabMat CLASSE 1°, 3° - INVALSI
Esercizi sui numeri, utili per le classi 1° e 3°.
Numeri (1) Scheda PDF del test 4
Numeri (2) Scheda PDF del test 3
29 novembre 2013 - LabMat CLASSE 1°, 3° - INVALSI
Esercizi su grafici e misure, utili per le classi 1° e 3°.
Test Dati e previsioni (1) - (interattivo con valutazione finale)
---
Una buona (?) notizia: per l’a. s. 2013-14 la prova Invalsi per le classi prime della scuola secondaria di primo grado non avrà luogo.
Per gli anni successivi, l'Invalsi sta studiando una collocazione alternativa del test nei mesi iniziali della scuola secondaria di primo grado.
(nota Invalsi prot. n. 0012537 del 18.11.2013).
24 novembre 2013 - LabMat CLASSE 1°, 3° - INVALSI
Esercizi sulle sequenze, utili per le classi 1° e 3°.
Test Relazioni e funzioni - Capire le sequenze
18 novembre 2013 - SEGNALAZIONI
Con grande piacere consiglio a tutti di visitare un giovane e promettente blog comparso nella rete l'8 ottobre 2013, sotto il segno della Bilancia: UnclePetros Blog.
I Blog nati sotto il segno della Bilancia sono straordinariamente intelligenti e capaci di comunicare in modi alternativi a quelli tradizionali.
Esprimono un incredibile amore per la giustizia. Hanno un grande spirito collaborativo e sono ispirati da sentimenti di equità. Possono diventare ribelli quando si rendono conto che le regole precostituite non sono quelle che rendono davvero giustizia agli individui.
I Blog di questo segno hanno inoltre un senso estetico eccezionale. Sono attratti dalla poesia e dalle arti grafiche. Adorano la simmetria.
(Profilo della Bilancia tratto e -molto- adattato da: http://oroscopo.d.repubblica.it/)
L'autore si firma UnclePetros, ma gli amici di BASE Cinque non tarderanno a riconoscerlo!
Segnalo Leggendo Archimede, un sito contenente 3 interessanti articoli tratti da un ebook di Luciano Ancora.
Ho aggiornato la pagina Il teorema cinese del resto correggendo un errore segnalatomi da Alessandro Scatolini. Grazie per la segnalazione!
16 novembre 2013 - GEOMETRIA SOLIDA - LabMat CLASSE 3°
Aggiornata la pagina del laboratorio, LabMat CLASSE 3° con una nuova attività.
18 ottobre 2013 - GEOMETRIA - SCIENZE
Nel bosco, ho trovato alcune conchiglie di chiocciole. Appartengono alla famiglia delle Elicidi ma quale sarà il genere? Helix, Cepa, Theba, ...?
Si dice che le conchiglie delle chiocciole hanno la forma di spirale logaritmica.
Conchiglia di chiocciola appartenente alla famiglia delle Elicidi (genere? specie?)
12 ottobre 2013 - UMORISMO
Aggiornata la pagina dell'umorismo matematico con un nuovo strabiliante fumetto!
(Ho usato e modificato alcune vignette di Randy Glasbergen - http://www.glasbergen.com/)
6 ottobre 2013 - SEGNALAZIONI
Annuncio telegrafico: è disponibile la versione 4.0.1 di Apache OpenOffice, qui: http://www.openoffice.org/it/.
Consiglio a tutti di scaricarla perché risolve alcuni (fastidiosi) problemini presenti nella versione 4.0.
3 ottobre 2013 - LabMat CLASSE 3° - GEOMETRIA SOLIDA
Una nuova attività aggiunta al LabMat CLASSE 3°.
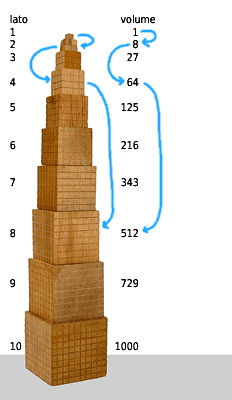
In un armadio della scuola abbiamo trovato una vecchia scatola di BAM (Blocchi Aritmetici Multibase) usati per attuare il cosiddetto metodo Zoltan Paul Dienes.
Fra questi bellissimi blocchetti di legno ci sono tutti i cubi da 1×1×1 a 10×10×10 cm.
Ci sono serviti prima di tutto per capire come si calcola il volume del cubo e poi per rispondere ad altre domande interessanti...
30 settembre 2013 - LabMat CLASSE 1°
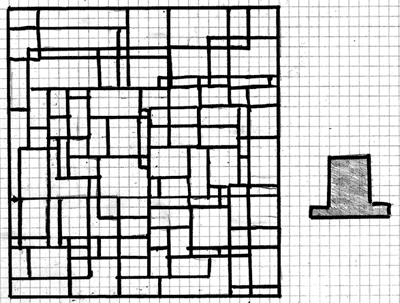
Nell'immagine qui sotto c'è un cappello nascosto come quello disegnato a lato.
Sei capace di trovarlo?
26 settembre 2013 - UMORISMO
La vignetta è di Emmanuel Chaunu. (Chaunu su Wikipedia, il blog di Chaunu)
23 settembre 2013- LabMat CLASSE 1°
La stella nascosta + (scheda PDF)
20 settembre 2013 - LabMat CLASSE 1°
Per eseguire calcoli mentali veloci e sicuri bisogna conoscere perfettamente le tavole della moltiplicazione (chiamate anche tabelline) e quelle dell'addizione.
Per allenarsi può essere utile:
ANGELO (javascript), allenatore di calcolo mentale sulle quattro operazioni, le potenze, i multipli e i divisori.
19 settembre 2013 - LabMat CLASSE 3°
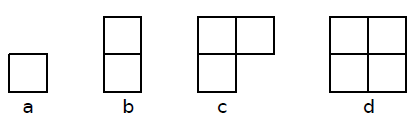
Quanti quadrati ci sono rispettivamente delle figure a, b, c, d?
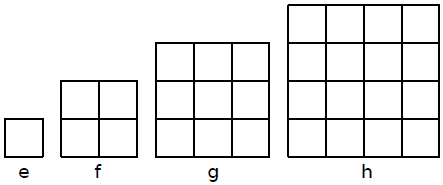
Quanti quadrati ci sono rispettivamente delle figure e, f, g, h?
12 settembre 2013 - SCUOLA
Tratto da George Polya, Mathematical discovery, 1962.
10 settembre 2013 - SCUOLA
La radice "competenz..." compare 109 volte nelle 68 pagine delle Indicazioni nazionali per il curricolo della scuola dell’infanzia e del primo ciclo d’istruzione (2012).
Alcune curiosità statistiche.
"Una scuola che intende educare istruendo non può ridurre tutto il percorso della conoscenza alla semplice acquisizione di competenze".
Il messaggio è chiaro: siamo nell'era della didattica per competenze. Da circa 7 anni. L'ha raccomandato il Parlamento Europeo nel 2006.
Ma cos'è la competenza matematica?
Di preciso, ma proprio di preciso, non lo so, tuttavia vi propongo una bozza di programmazione relativa al primo anno di scuola media (secondaria di primo grado).
Scuola secondaria di primo grado, programmazione curricolare di Matematica.
Per ora il file contiene soltanto la Premessa generale, la Programmazione per la classe prima, e le Appendici.
5 settembre 2013 - SCUOLA - UMORISMO
La scuola è ufficialmente iniziata, per i prof!
Ma... chi è l'attuale Ministro dell'Istruzione, dell'Università e della Ricerca?
(risposta in fondo al post)
---------
Per l'occasione, ho aggiornato la breve storia di un problema-chiave dell'ultimo mezzo secolo di scuola: il problema delle patate.
Il professore di matematica entra in classe e attiva il suo tablet collegato alla rete wireless della scuola. Dopo qualche minuto è in grado di compilare il registro e trasferire i dati in una cloud, con semplici ripetitive e ossessive finger gestures sul touch-screen.
Nel frattempo, l'alunno incaricato tira giù le tapparelle e accende la LIM (Lavagna Interattiva Multimediale - 800x600) grazie alla quale si può fare l'esperienza dell'augmented reality inserita in un learning-object.
Tutti i 30 alunni accendono i loro tablet e si preparano ad aprire l'e-book di e-matematica o a prendere appunti strofinando il loro dito indice (e a volte anche il pollice) sul touch-screen. Se teniamo conto che ci sono anche 30 smarthphone accesi nelle tasche degli alunni, il livello delle onde elettromagnetiche a radio frequenza è decisamente alto. Ma nessuno se ne accorge.
Il professore gesticola sullo schermo della LIM ed ecco che appare una enorme patata, una patata aumentata che sembra in 3D e ruota per tutti i versi seguendo alcune body gestures del professore stesso. Volendo, si può anche sbucciare, tagliare a fettine e friggere, virtualmente. Questo si chiama wow-effect.
Poi il professore shrinka la patata, la dragga lateralmente e la droppa in un angolo della LIM.
Finalmente inizia a scrivere, usando il suo dito indice invece del gesso1. Ecco ciò che compare sulla LIM:
Il professore, sempre gesticolando sulla LIM, invia il testo, sotto forma di immagine gif - 400x190, per e-mail agli alunni, che lo scaricano sui loro tablet e iniziano a risolverlo. Ma questa è la cosa meno importante.
---------
Note.
1gesso, è l'unica parola straniera usata in questo articolo. Il gesso era un bastoncino bianco di solfato di calcio diidrato, o anche carbonato di calcio, che serviva per scrivere su lastre nere di ardesia chiamate lavagne. Le scritte si potevano cancellare perfettamente con speciali rotoli di panno. La lavagna quindi era una memoria di massa riscrivibile milioni di volte. Praticamente gratis.
---------
A tutti i colleghi insegnanti, agli studenti e ai genitori
auguro un anno scolastico pieno di successi!
Nelle vostre programmazioni prevedete di far sorridere gli alunni almeno una volta ogni lezione!
---------
Maria Chiara Carrozza
PD, Ministro dell'Istruzione, dell'Università e della Ricerca,
17° Legislatura, Governo Letta, dal 23 aprile 2013.
Seguitela su Twitter: MC_Carro. Comprese le risposte ai suoi tweet.
29 agosto 2013 - UMORISMO
Aggiornata la pagina: Umorismo matematico 2013.
Un'immagine un po' sfocata di una scuola d'altri tempi.
Condiviso su Google+ da Matematica? Absolutamente!
12 agosto 2013 - SCUOLA - SCIENZE - SEGNALAZIONI
Le uova, assieme alle galline, sono temi che ogni tanto ritornano su BASE Cinque, per i loro profondi collegamenti con la scienza, la filosofia, la matematica nonché la gastronomia.
In questo breve articolo ho ripresentato la grande sfida dell'uovo in piedi, senza dimenticare il suo lato artistico.
Anche da qui lancio un invito a tutti voi: se avete realizzato qualche meraviglioso equilibrio con le uova, non esitate a fotografarlo e inviarmi il magico scatto!
9 agosto 2013 - UMORISMO - SEGNALAZIONI
I matematici (e forse anche i fisici) talvolta semplificano troppo la realtà per semplificare i loro calcoli.
Così capita di leggere teoremi che iniziano: "Supponiamo che la mucca sia sferica..."
Ecco cosa potrebbe succedere se gli animali della giungla mangiassero tutti al più noto fast food del mondo.
Video su YouTube: ROLLIN' SAFARI - what if animals were round?
Fotogramma tratto dal video "Rollin`Safari", Flying Stone GbR, 2012.
7 agosto 2013 - SCUOLA - SCIENZE - SEGNALAZIONI
Riconoscete il contenitore delle fotografie seguenti? È’ il flacone di un noto prodotto per la pulizia della lavastoviglie. Ha la forma di un quasi-parallelepipedo di circa 13 x 10 x 2 cm.
Come oggetto scientifico è irresistibile.
Se ne avete a disposizione uno vuoto, potete utilizzarlo per fare vari esperimenti sulle proprietà dei liquidi.
Per esempio, potete riempirlo per 1/4 d'acqua colorata e farlo ruotare attorno al suo asse verticale.
La superficie del liquido, invece di rimanere piana e orizzontale, formerà una parabola (figg. 3, 4, 5). Perché?
Per farlo ruotare, potete montarlo sul coperchio girevole di una centrifuga per insalata! Fissatelo per bene con del nastro bi-adesivo come mostrato in fig. 2.
Nelle immagini 4 e 5 il flacone sembra fermo, perchè è stato bloccato dallo scatto fotografico, ma in realtà sta ruotando come una trottola.
1 agosto 2013 - GIOCHI
Grazie a Luigi C. per avermi suggerito alcune correzioni da apportare alla Guida al cubo di Rubik. Ho aggiornato la pagina.
31 luglio 2013 - ARITMETICA
Sette domande matematiche sul racconto I sette messaggeri, di Dino Buzzati.
Un principe parte dalla capitale per raggiungere i confini del regno di suo padre.
Porta con sé una scorta di fedeli cavalieri fra i quali sceglie sette messaggeri che facciano la spola tra lui e la capitale, per comunicare con i suoi cari.
Per distinguerli più facilmente impone loro nomi con le iniziali alfabeticamente progressive: Alessandro, Bartolomeo, Caio, Domenico, Ettore, Federico, Gregorio.
Con il passare dei giorni, dei mesi e degli anni, la distanza si fa sempre più grande e le comunicazioni sempre piu rare...
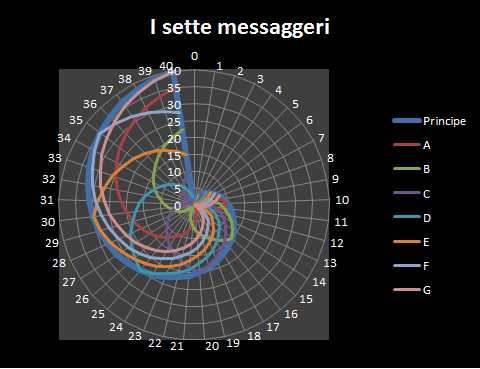
I primi 40 giorni di viaggio dei 7 messaggri in coordinate polari.
27 luglio 2013 - SEGNALAZIONI
Annuncio telegrafico: è disponibile la versione 4.0 di Apache OpenOffice, qui www.openoffice.it.
Cose che si notano subito: miglioramenti all'interfaccia, alla velocità, al componente Draw, per il disegno vettoriale.
Purtroppo non ci sono novità su Math, l'editor di formule matematiche. E neppure ne sono previste, al momento, per la versione 4.1.
25 luglio 2013 - GEOMETRIA - COMBINATORIA - GRANDI MAESTRI
E' uno dei quesiti più conosciuti al mondo ma ci sono delle novità.
Per chi si fosse sintonizzato solo ora, riporto il testo del problema nella
sua formulazione di base.
Il problema di base
Ci sono 9 punti su un piano disposti in una griglia quadrata 3×3.
Il problema consiste nel disegnare una linea spezzata formata da 4 segmenti che passi attraverso tutti i nove punti.
La linea deve attraversare ogni punto una sola volta.
Qui sotto vedete la griglia 3×3 e a fianco una soluzione errata perché la linea è formata da 5 segmenti invece dei 4 richiesti.
Qual è la soluzione esatta?
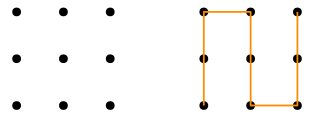
Una sfida in più
Questa volta avete 16 punti su un piano disposti in una griglia quadrata 4×4.
Il problema consiste nel disegnare una linea spezzata formata dal minimo numero possibile di segmenti che passi attraverso tutti i 16 punti.
Qual è tale numero minimo?
Marco Ripà e Pablo Ramirez hanno esteso il problema a una griglia quadrata di N×N punti nel piano e a una griglia cubica di N×N×N punti nello spazio. E sono andati anche oltre: hanno spiegato come sia possibile risolvere questo puzzle negli spazi a più di tre dimensioni.
I risultati delle loro ricerche si trovano nei seguenti articoli:
1) Marco Ripà e Pablo Ramirez, Il Nine Dots Puzzle esteso a N×N×...×N punti.
2) Marco Ripà, Nine Dots Puzzle extended to N1×N2×...×Nk points under house arrest.
Le origini
Per risolvere questo problema bisogna pensare fuori dalla scatola (think out of the box).
Ciò significa che non dobbiamo farci condizionare dai confini della griglia. Le linee da tracciare possono uscire da questi confini.
Un problema simile a questo fu posto per la prima volta da Samuel Loyd e si trova nella sua Cyclopedia of Puzzles pubblicata nel 1914.
E Samuel Loyd, a sua volta, si ispirò al cosiddetto uovo di Colombo.
Ma chi sono gli strani personaggi che compaiono nel disegno?
Figura tratta da Samuel Loyd, Cyclopedia of Puzzles, New York, 1914, pag 301.
20 luglio 2013 - SCIENZE
A tutti gli insegnanti di scienze, a tutti i genitori, ai nonni, agli zii, a tutti i ragazzi ingegnosi, segnalo un sito indiano che mi ha davvero commosso: Toys from trash.
Letteralmente si traduce giocattoli dalla spazzatura ma in realtà
gli autori di questo sito sono andati ben oltre oltre: ci insegnano
come è possibile fare grande scienza con semplici oggetti di uso
comune.
Gli autori del sito, da destra: Dr. Ashok Rupner, Dr. Arvind Gupta, Dr. Vidula Mhaiskar.
18 luglio 2013 - ARITMETICA
Ogni numero razionale si può scrivere in molti modi. Anzi, infiniti.
Per esempio:
0,5 = 1/2 = 2/4 = 3/6 = ...
Fin qui, tutto normale, nessuno si stupisce del fatto che 0,5 possa mascherarsi in infiniti modi continuando però a essere lo stesso numero.
Ma fra questi modi ce n'é uno che non convince la gente:
0,5 = 0,49999999... (la cifra 9 si ripete infinite volte)
Quest'ultima doppia forma vale per tutti i numeri decimali non periodici: si possono scrivere in forma periodica con periodo 9.
Il caso più famoso è:
0,9999999... = 1
Dimostralo.
Le risposte sono diverse, a seconda del contesto:
0,9999999... < 1.
Vedi: Karin Usadi Katz and Mikhail G. Katz, A strict Non-Standard inequality .999. . . < 1, pubblicato su arXiv.org il 24 febbraio 2009.
9 luglio 2013 - MULTIDISCIPLINARE
Immagine tratta da: ChristArt
Cari amici,
auguro a tutti voi felici vacanze
dovunque voi siate,
ai monti, al mare, in campagna, in città!
COMPITO PER LE VACANZE
Fate una Web-Quest e cercate di spiegare...
1) Il problema di Monthy Hall
2) 0,999999... = 1
3) Ci sono tanti numeri pari quanti numeri naturali
4) La legge di Benford
5) Il paradosso del compleanno
6) Il paradosso dell'idraulico
7) Il paradosso di Bertrand
8) Calcolare pi-greco con un tiro a segno per freccette
9) La serie armonica diverge
10) Probabilmente i tuoi amici sono più popolari di te nei social network
11) Congiungendo i punti medi di un qualsiasi quadrilatero, anche del più sgangherato, si ottiene sempre un parallelogrammo perfetto.
12) Il problema del condannato perdonato.
Vi suggerisco questo punto di partenza:
The 12 Most Controversial Facts In Mathematics
Se avete altri fatti da aggiungere alla lista, inviatemi una e-mail.
6 luglio 2013 - GEOMETRIA SOLIDA - ARITMETICA
Un mini-poster quasi senza parole per illustrare il seguente...
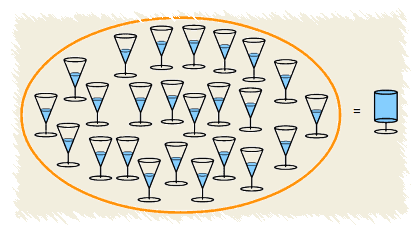
Teorema: I volumi di due coni simili stanno fra di loro come i cubi delle loro altezze o come i cubi dei loro raggi.
5 luglio 2013 - SCUOLA - SCIENZE - SEGNALAZIONI
Valutare la metà di qualcosa non è sempre facile come sembra.
Per esempio, a quale livello si trova la metà di un bicchiere conico?
2 luglio 2013 - SCUOLA - SCIENZE - SEGNALAZIONI
Avete mai notato quelle affascinanti perle d’acqua che si formano sulle foglie di alcune piante dopo la pioggia? Questo fenomeno è spettacolare sulle grandi foglie del Loto ma lo possiamo osservare anche su piante più diffuse in Italia, come l’Echeveria, il Graptopetalum e il Cavolo.
22 giugno 2013 - SCUOLA - SCIENZE - SEGNALAZIONI
Terza e ultima puntata del viaggio nel mondo degli alberi urbani: dedicata agli alberi improbabili.
8 giugno 2013 - SCUOLA - SCIENZE - SEGNALAZIONI
Continua il viaggio nel mondo degli alberi urbani. Un'esperienza che propongo a tutti gli insegnanti di Scienze e più in generale a tutte le persone.
3 giugno 2013 - SEGNALAZIONI
Cari amici, grazie al lavoro di Pietro Vitelli, il Forum di BASE Cinque è completamente rinnovato. Le principali novità sono:
Conoscete un problema interessante (e divertente) da proporre? Volete lanciare una sfida? Avete un dubbio di matematica? Volete segnalare un sito, un libro, un filmato di argomento matematico?
Non esitate, iscrivetevi al Forum e condividete le vostre idee.
1 giugno 2013 - SCUOLA - SCIENZE - SEGNALAZIONI
Infilate una moneta da 10 centesimi (di Euro) in un palloncino, gonfiate il palloncino e fate rotolare velocemente la moneta al suo interno come una moto che corre in una gabbia sferica.
Sentirete un suono che ricorda il volo di un calabrone.
E' questo un punto di partenza per affrontare tanti argomenti di fisica e matematica mettendo in gioco tutti i cinque sensi e oltre.
25 maggio 2013 - GEOMETRIA
Un trucco di magia basato al 100% sulla matematica.
Osservate il filmato The missing piece, tratto dal sito Quirkology, e cercate di scoprire come funziona.
Non richiede particolari abilità e si può costruire facilmente con un cartoncino.
23 maggio 2013 - SEGNALAZIONI
Grazie a Ivana Niccolai per aver segnalato al Forum il nuovo libro di Giorgio Dendi.
Giorgio Dendi, La Matematica è divertente - Voglio vincere i Mondiali di Matematica!, Digital Index Editore, Modena, 2013. ISBN 9788897982609, Formato epub 2 con video e animazioni.
Una esauriente presentazione del libro si trova nel sito Digital Docet.
Per chi non conosce il simpaticissimo Giorgio Dendi, riporto alcune notizie biografiche.
Giorgio Dendi è noto enigmista ed esperto di giochi quali cruciverba e crittografie. Nel 2000, dopo aver vinto i Campionati Italiani di Giochi Matematici, si aggiudica il titolo internazionale a Parigi. Dal 2002 è nello staff dei preparatori della Nazionale Italiana di Giochi Matematici, che ha contribuito a portare a molte vittorie. Promuove e diffonde la matematica ricreativa, l'enigmistica e la divulgazione.
Giorgio Dendi alla finale internazionale dei Giochi matematici del 2011, Parigi.
22 maggio 2013 - ARITMETICA - SEGNALAZIONI
Mi sono distratto qualche giorno...
... e nel mondo della matematica (ricreativa) sono successe un sacco di cose straordinarie. Vediamone due.
Definizione. Due numeri primi consecutivi sono detti gemelli quando la loro differenza è pari a 2.
Congettura. Esistono infinite coppie di numeri primi gemelli.
Il matematico cinese Yitang Zhang ha dimostrato che esistono infinite coppie di numeri primi che distano fra di loro almeno 70 000 000.
Un passo avanti verso la dimostrazione della congettura dei numeri primi gemelli.
L'articolo, intitolato Bounded gaps between primes è pubblicato sugli Annals of Mathematics del Department of Mathematics at Princeton University. Purtroppo non è gratuito.
Yitang Zhang
Finalmente possiamo scrivere:
Teorema: Ogni numero dispari maggiore di 7 può essere espresso come somma di tre numeri primi dispari.
Oppure, equivalentemente: Ogni numero dispari maggiore di 5 può essere espresso come somma di tre numeri primi.
Il matematico peruviano Harald Andrés Helfgott ha dimostrato la congettura debole di Goldbach. L'articolo di Helfgott è pubblicato su http://arxiv.org/.
In questa pagina di BASE Cinque c'è un programmino in javascript per fare esperimenti con questa congettura, che non più una congettura.
Harald Andrés Helfgott
14 maggio 2013 - SCIENZE - SEGNALAZIONI
Nelle nostre città ci sono moltissimi alberi.
Se ne stanno buoni buoni, fermi al loro posto dove ogni mattina ci danno il buongiorno. Si regolano sempre sull'ora solare e compiono in silenzio la seguente trasformazione chimica: 6H2O + 6CO2 --> C6H12O6 + 6O2.
E noi li conosciamo almeno un po'?
Segnalo a tutti gli amici e ai colleghi docenti di scienze, l'articolo Alberi in città (parte 1°) dal blog invitoallanatura.it.
10 maggio 2013 - ARITMETICA
Sì, è proprio così: Rascal, non Pascal.
Tutto è iniziato da questa semplice domanda: nel seguente triangolo numerico, quali numeri scrivereste al posto dei punti interrogativi?
1
1 1
1 2 1
1 3 3 1
? ? ? ? ? ?
Tre ragazzi di scuola media abitanti in tre diverse parti del mondo hanno dato una risposta inaspettata alla domanda. Dalla loro collaborazione in rete è nata una nuova e significativa sequenza numerica presentata nell'articolo che vi propongo (in inglese). I tre ragazzi sono Alif Anggoro, Eddy Liu e Angus Tulloch.
L'articolo mi è stato segnalato da Roberto Doniez.
La risposta dei tre ragazzi è 1, 4, 5, 4, 1.
E la riga successiva è 1, 5, 7, 7, 5, 1.
E la riga successiva è ...
Come si spiega?
8 maggio 2013 - SEGNALAZIONI
Segnalo due nuovi blog, giovani e davvero promettenti.
Associazione culturale Festa Mentis - Tutto è numero
Blog dell'associazione fondata da Giorgio Dendi, Paolo Pizzorni, Giuseppe Rosolini, Nadia Trucco e Omar Valentino.
Matematizzando - La bellezza della matematica
Blog creato e gestito da Ivana Niccolai. Presenta, tra l'altro, bellissime animazioni su argomenti di geometria e teoria dei grafi.
6 maggio 2013 - IL LATO COMICO
32. Quante gambe hai?
La statistica dimostra che la maggioranza delle persone ha un numero di gambe leggermente superiore alla media.
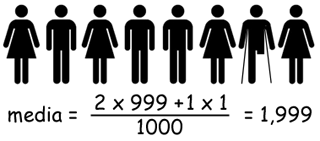
(tratto da: Matematica? Absolutamente!)
31. Triste verità statistica
La statistica dimostra che l'essere umano medio ha un testicolo.
(tratto da: Matematica? Absolutamente!)
30.Cambiano solo i numeri
Il professore disse che gli esercizi da fare a casa erano uguali a quelli fatti a scuola. Cambiavano solo i numeri. Tranne π (pi-greco).
29. Mettere in forno a 120 gradi
(tratto da: Matematica? Absolutamente!)
28. Dimostrazione che 1/2+1/3=2/5
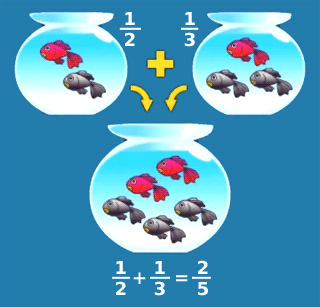
(tratto da: Matematica? Absolutamente!)
4 maggio 2013 - IL LATO COMICO
27. Terrificante 3
Qual è il poligono più rumoroso?
Il rombo.
26. Terrificante 2
Professore: "Anche oggi hai dimenticato di portare il libro di matematica!"
Alunno: "E' andato dallo psicanalista."
Professore: "Perché?"
Alunno: "Aveva troppi problemi."
25. Terrificante 1
La sfera non si può sviluppare sul piano.
Ma si potrà sviluppare su una chitarra?
2 maggio 2013 - ARITMETICA
Per trovare facilmente i primi elementi della serie di Fibonacci nei fiori conviene andare in un vivaio di piante per il giardino.
Lo so, i puristi protesteranno perché nel caso della Bougainvillea e dello Spathiphyllum non ho considerato i petali ma le brattee, le quali sono foglie modificate che circondano il vero fiore. Ma si può sempre migliorare...
Chiunque abbia suggerimenti in proposito è pregato di comunicarmeli o inviarli al Forum: cerco fiori da 1, 2, 3 petali.
30 aprile 2013 - IL LATO COMICO
24. Le prime lezioni di matematica
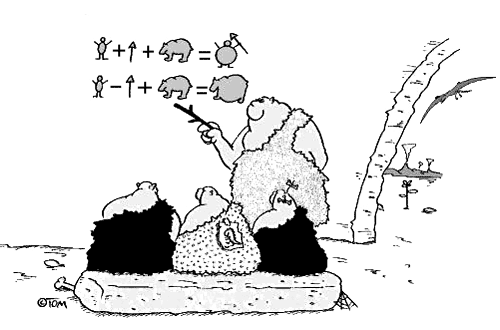
(tratto da: Matemática? Absolutamente! su Google+)
23. Autoritratto di pi-greco
(tratto da: Matemática? Absolutamente! su Google+)
22. Umorismo raffinato di Google
Se digitate su Google la parola "recursion", Google vi risponde:
"Forse cercavi: recursion"
Ecco la prova!
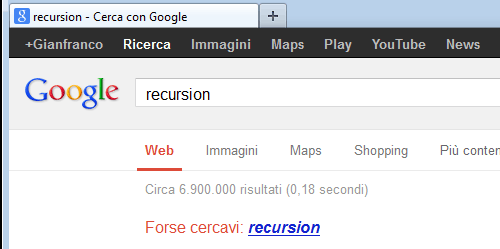
29 aprile 2013 - ARITMETICA
Ho fatto un giro in campagna e ho fotografato questi fiori.
Mi mancano quelli da 0, 1, 1, 2, 3 petali. E magari anche quelli da 34 e 55 petali.
27 aprile 2013 - RITRATTI
Ho aggiornato la Galleria di ritratti di matematici con un ritratto di Andrei Andreyevich Markov (1856-1922).
24 aprile 2013 - AGGIORNAMENTI
Prova nazionale INVALSI 2007-2008_(web)
Prova nazionale INVALSI 2007-2008_(odf)
Ho inserito in una unica pagina la prova nazionale INVALSI 2007-2008 (terza media), con alcuni suggerimenti e le soluzioni.
Ho inoltre preparato una scheda in formato odf concentrata in 4 pagine, contenente quasi tutti i quesiti della prova. E' utile per risparmiare fotocopie.
Nota. Il formato odf (open document format) si può aprire e modificare con Apache Open Office e Libre Office.
20 aprile 2013 - IL LATO COMICO
21. Quesito a risposta multipla
Quale delle seguenti cose è la più diversa dalle altre?
(A) Una laurea in Biologia Matematica
(B) Una laurea in Matematica Teorica
(C) Una laurea in Statistica
(D) Una grande pizza ai peperoni
Risposta: (B) - le altre tre possono nutrire una famiglia di quattro persone.
(tratto da Physics su Google+)
20. Georg Cantor a scuola
"Pssst... Georg, che risultato ti è venuto nel secondo esercizio?"
"Infinito."
"Solo?"
19. Metodi anticoncezionali
E' ormai permesso alle donne cattoliche di evitare una gravidanza ricorrrendo alla matematica, ma non è loro ancora concesso di ricorrere alla fisica o alla chimica. (Henry Louis Mencken via DrZap)
18. Il colmo per un matematico
Sedersi alla tavola pitagorica e mangiare una radice quadrata.
17. Premio Ig-nobel 2009 per la Matematica
Premiato Gideon Ono, governatore della Banca Centrale dello Zimbabwe. Ha dato modo a tutta la popolazione di imparare i numeri stampando banconote che andavano da un centesimo a cento miliardi di dollari (zimbabwiani).
(E' un fatto veramente accaduto, se non ci credete visitate il sito ufficiale del Premio Ig-Nobel, 2009)
Alcuni assegni al portatore stampati dalla Reserve Bank of Zimbabwe tra il luglio 2007 e il luglio 2008, oggi scaduti, che illustrano il tasso di iperinflazione nello Zimbabwe. Fonte Wikipedia.
19 aprile 2013 - IL LATO COMICO
Cari visitatori, in questo periodo ho bisogno di sorridere un po'. E voi?
Per questo vi consiglio la sezione Matematica del sito di Franco DrZap.
Nel frattempo continuerò a proporvi le migliori battute di umorismo matematico.
16. Taxi
Ieri ho preso un taxi e mi è costato 60 EURO. Siccome ne avevo solo 54 ho chiesto al tassista di fare 6 EURO di marcia indietro. (Fichi d'India)
15. Il calcolatore umano
Lo chiamavano il calcolatore umano. Senza guanti, sapeva contare fino a 10. Scalzo, sapeva contare fino a 20. Nudo, arrivava a 21. (http://www.drzap.it/matematica.htm)
14. Addizione algebrica
In un'aula ci sono 25 alunni. Durante l'intervallo ne escono 30. Quanti alunni bisogna far entrare affinché l'aula sia vuota?
13. Coppia russa
"Boris, per favore, vai a comprare un paio di bottiglie di Vodka."
"Quanto è un paio?"
"Sette."
18 aprile 2013 - IL LATO COMICO
12. Esponenziale
Immaginate di camminare sull'asse x di un piano cartesiano partendo dall'origine e procedendo in verso positivo alla velocità di un metro al secondo (1 m/s).
Mentre voi camminate, si traccia il grafico della funzione y=ex.
---
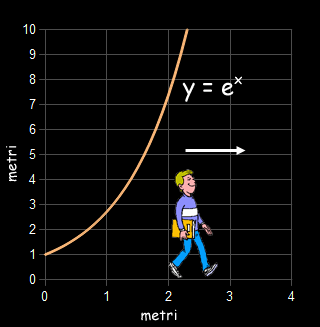
Quando siete a circa 20 m alla destra dell'origine...
---
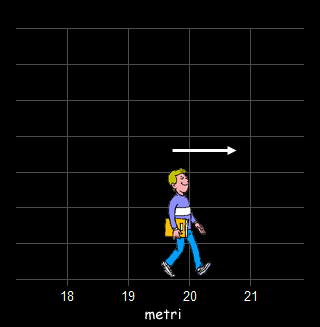
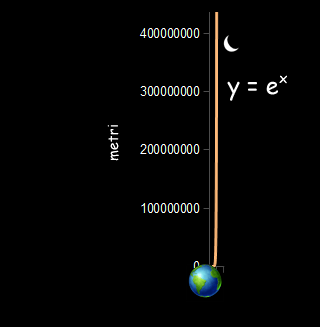
...il grafico della funzione y=ex ha già superato la Luna e sta volando alla velocità della luce.
Ma subito dopo è molto, molto più distante e veloce.
11. Qualcosa di proibito
Sabato i miei genitori non sono a casa, facciamo qualcosa di proibito?
Sì, dài, dividiamo per zero!
D'accordo, ma questa volta io sto al numeratore!
10. Coltivazione
Perché non si può coltivare il grano in Z/6Z?
Perché non è un campo.
9. Dilemma
Che cosa è un dilemma?
Un lemma che dimostra due risultati.
16 aprile 2013 - IL LATO COMICO
8. Ritardo autoreferenziale
Torno fra cinque minuti. Se sono in ritardo, rileggete questo messaggio.
7. Ieri, oggi, domani
Solo ieri, oggi era domani.
Solo domani, oggi sarà ieri.
Solo oggi, oggi è oggi.
6. Che giorno è oggi?
"Che giorno è oggi?"
"Non lo so."
"Ma, hai un giornale in tasca."
"E' inutile. E' di ieri."
(Attribuita a Raymond Smullyan)
5. Matematici al bar
Un'infinità numerabile di matematici entra in un bar.
Il primo matematico ordina una birra.
Il secondo ordina mezza birra.
Il terzo ordina un quarto di birra.
Il quarto ordina un ottavo di birra.
Il barista, a questo punto, dice: "Ok, ho capito!" e versa due birre.
15 aprile 2013 - IL LATO COMICO
4. Il volume della pizza
Qual è il volume di una pizza di raggio z e altezza a?
pi z z a.
3. Algebra delle mele
Quanto fa 2 mele + 3 mele?
5mle2.
2. Equazioni romane
Perché gli antichi Romani consideravano l'algebra poco interessante?
Perché per loro X valeva sempre 10.
1. Permutazioni
Elenca tutte le permutazioni di {7, 0, 0}.
700, 070, James Bond.
10 aprile 2013 - ARITMETICA
Sofia ha una collezione di calcolatrici speciali. Una di queste è dotata soltanto di due tasti: [+1] e [×2].
Quando premi uno dei due tasti, la calcolatrice mostra automaticamente il risultato sullo schermo.
Per esempio, se all'inizio sullo schermo c'è il numero 9 e premi il tasto [+1], il risultato diventa 10.
Se poi premi il tasto [×2], il risultato mostrato è 20.
Ecco due domande. Se cominci con il numero 0, quanti tasti dovrai premere come minimo per ottenere 100? E per ottenere 1000?
Tratto da MinuteMath, 8 aprile 2013
Fai i tuoi esperimenti con la calcolatrice qui sotto!
27 marzo 2013 - ARITMETICA
Ho cercato in internet il Teorema di Pitagora e ho ottenuto due milioni di risultati.
Ho cercato in internet l'espressione 6÷2(1+2) e ho ottenuto un miliardo di risultati.
credit: Bill Watterson
E' da quattro anni che il 20% dell'umanità si chiede quanto fa questa espressione aritmetica. Hanno provato a calcolarla con innumerevoli calcolatrici, hanno consultato ingegneri nucleari, ne hanno discusso nei forum matematici più autorevoli e alla fine gli è sfuggita di mano: l'espressione è dilagata su Facebook.
Ma rimangono ancora dei dubbi.
Suggerimento
Nell'espressione c'è un segno sottinteso di moltiplicazione.
6 : 2 × (1 + 2) =
6 : 2 × 3 = (precedenza alle parentesi tonde)
3 × 3 = (precedenza alla divisione)
9
Quando in una espressione compaiono tre o più operazioni × e : di seguito, devono essere eseguite nell'ordine in cui sono scritte, procedendo da sinistra verso destra.
Il segno ÷ si chiama obelus o obelo e rappresenta l'operazione di divisione. Tuttavia, secondo la normativa ISO 80000-2:2009, non dovrebbe essere usato.
Sempre secondo tale normativa, i segni ammessi per le quattro operazioni sono:
Il segno : indica un rapporto. Per esempio, il rapporto fra una qualunque circonferenza C e il suo diametro d è pi-greco:
C : d = π
25 marzo 2013 - SOFTWARE - GRAFICA
Finalmente, dopo circa due anni di attesa, è uscita la versione 7.1 per Windows di IPE extensible drawing editor, un ottimo programma free e open-source di disegno vettoriale.
Il programma supporta LaTeX e può salvare i file in formato .ipe xml, .eps e .pdf.
Su sourceforge.net si trovano il sito di IPE e i files da scaricare.
Grazie Otfried Cheong!
23 marzo 2013 - SCUOLA
Oggi, le parole chiave della scuola digitale sono: LIM, Cl@ssi 2.0, Editoria digitale.
Secondo questa trilogia, l'educazione degli alunni e lo sviluppo delle loro competenze fondamentali sarebbero legati all'uso di oggetti e servizi tecnologici, prevalentemente informatici. Oggetti e servizi che obbediscono e ci inducono a obbedire alle leggi del mercato.
Oggetti e servizi che ingigantiscono l'impronta ecologica di una parte dell'umanità: tenere acceso internet costa circa 300 Gigawatt di potenza elettrica costante. E' tanto? E' poco? E' più o meno come 10 volte l'Italia. E nel 2016 sarà il quadruplo.
Per i consumi mondiali di internet, vedi: Barath Raghavan and Justin Ma, The Energy and Emergy of the Internet, ICSI and UC Berkeley.
(vedi il filmato su YouTube)
A Nuova Delhi, in India, Rajesh Kumar Sharma ha fondato una scuola gratuita che dà istruzione a una trentina di bambini appartenenti agli ambienti più poveri della città. La scuola si trova sotto un ponte della metropolitana, senza muri, né banchi, né sedie, né riscaldamento. Ci sono tre grandi lavagne dipinte nel cemento armato.
La situazione è drammatica, ma gli alunni sorridono e seguono con interesse le lezioni del maestro. E' una lezione anche per noi.
8 - 18 marzo 2013 - ALLENAMENTO PROVE INVALSI (1-7)
Ho inserito in una unica pagina la prova nazionale INVALSI 2007-2008 (terza media), con alcuni suggerimenti e le soluzioni.
Prova nazionale INVALSI 2007-2008_(web)
Prova nazionale INVALSI 2007-2008_(odf)
3 marzo 2013 - RITRATTI
Ho aggiornato la Galleria di ritratti di matematici con due fotografie di Paul Erdos e Norman Anning.
Paul Erdos (1913-1996) |
Norman Anning (1883-1963) |
Teorema di Erdos-Anning (1945)
Nel 1945 Erdos aveva 32 anni mentre Anning ne aveva 62.
2 marzo 2013 - GEOMETRIA - ARITMETICA
...nella versione originale in inglese.
---
Per qualunque n (finito) è possibile trovare n punti nel piano, non tutti su una stessa linea retta, tali che le loro reciproche distanze siano tutte numeri interi.
---
Il testo dice "non tutti su una stessa retta" ma nella dimostrazione si fa vedere come costruire un insieme di n punti, tutti a distanze intere fra di loro, dei quali nessuna terna giaccia sulla stessa retta.
La dimostrazione usa due teoremi:
Teorema 1.
Il quadrato di ogni numero primo p della forma 4 k +1 si può esprimere come somma di due quadrati di numeri interi.
p 2 = a 2+ b 2
Teorema 2 (Tolomeo).
In ogni quadrilatero inscritto in una circonferenza, la somma dei prodotti delle coppie di lati opposti è uguale al prodotto delle diagonali.
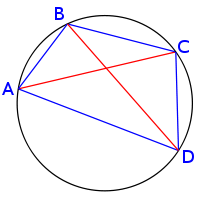
AB × CD + BC × AD = AC × BD
26 febbraio 2013 - GEOMETRIA - ARITMETICA
Siete capaci di posizionare 6 punti su un piano in modo che la distanza tra ciascuna coppia di essi sia un numero intero e non ce ne siano tre allineati?
Precisazioni.
Una possibile generalizzazione: è possibile posizionare in un piano 7, 8, 9, ..., n punti con lo stesso criterio?
Qui sotto vedete due esempi con 4 e 3 punti.
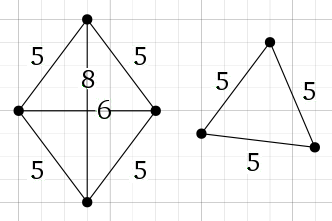
22 febbraio 2013 - AGGIORNAMENTO
Ho corretto il programma javascript della pagina Le terne pitagoriche che non funzionava su Firefox a causa di un problema con il comando onclick .
L'interprete javascript di Firefox è davvero veloce. Mi ha permesso di ampliare di un fattore 5 la dimensione delle terne da ricercare.
16 febbraio 2013 - GEOMETRIA COMBINATORIA
Segnalo il blog MATEMATIZZANDO - La bellezza della matematica di Ivana Niccolai.
In particolare, il post dedicato ai cammini euleriani mi ha ispirato il seguente problemino.
Osservate la figura qui sotto. E' formata da 12 segmenti e 8 vertici (indicati con cerchietti).
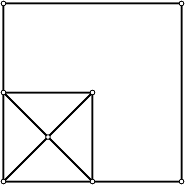
Esercizio 1. Sapreste disegnare la figura con un solo
tratto di penna, senza mai staccare la penna dal foglio e percorrendo ogni
segmento una sola volta?
Una difficoltà in più: ad ogni incrocio dovete cambiare direzione.
Se ci riuscite, avete fatto un cammino euleriano (da Leonard Euler ).
Esercizio 2. Sapreste tracciare un percorso, seguendo i lati della figura, che passi per tutti i vertici esattamente una volta? Il percorso non deve necessariamente passare per tutti i lati.
Se ci riuscite, avete fatto un cammino hamiltoniano (da William Hamilton )
15 febbraio 2013 - SEGNALAZIONI DAL FORUM
Veronica De Blasio, Sulla funzione di partizione , sintesi della tesi di laurea, Università degli Studi Roma Tre, Facolta di Scienze Matematiche, Fisiche e Naturali, Corso di Laurea Magistrale in Matematica, a. a. 2010-2011, relatore Prof. Andrea Bruno.
Eulalia Giglio, Le serie di Farey , tesi di laurea, Università degli Studi di Padova, Facolta di Scienze Matematiche, Fisiche e Naturali, Corso di Laurea in Matematica, a. a. 2002-2003, relatore Prof. Benedetto Scimemi.
Grazie a Quelo-Sergio per un programma in Decimal Basic che genera le sequenze di Farey.
11 febbraio 2013 - ARITMETICA
Risolvendo un problema combinatorio mi sono imbattuto nelle partizioni additive dei numeri interi . Poiché non ho trovato un'applicazione online che genera le partizioni di un intero, ne ho costruito una in javascript e la propongo qui, per chi ne avesse bisogno.
3 febbraio 2013 - LIBRI
Peppe segnala nel Forum un ottimo libro pensato come supporto per lo studente che intende prepararsi per le olimpiadi della matematica, e cerca una solida base di teoria prima di affrontare i problemi proposti.
A. Astolfi, G. Audrito, A. Carignano, F. Tanturri, Dispense di Matematica Olimpionica , seconda edizione riveduta e ampliata da G. Audrito, G. Distefano, R.Maffucci, L. Prelli, F. Roman, Associazione Subalpina Mathesis - Sezione Bettazzi - 2011
30 gennaio 2013 - AGGIORNAMENTI
Aggiornate le pagine dei problemi tratti da Henry Ernest Dudeney, Amusements in Mathematics , 1917:
con le soluzioni.
28 gennaio 2013 - ARITMETICA
Provo a riscrivere in chiave moderna il problema dei quattro 7 di Dudeney. Così mi sembra più chiaro e verificabile direttamente. Basta avere una calcolatrice.
---
Avete una calcolatrice tascabile non scientifica, come quella della foto qui sotto.
Il vostro compito è quello di ottenere il risultato 100 scritto sul visore.
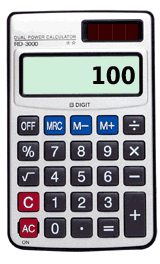
27 gennaio 2013 - ARITMETICA
Il professor Rackbrane ha dimostrato alla lavagna in che modo si possono usare quattro 5 e le operazioni aritmetiche per ottenere 100.
Ora vi chiede: scrivete quattro 7 e gli opportuni segni aritmetici in modo da ottenere 100.
Con quattro 9 sarebbe stato più facile, ma i quattro 7 richiedono una buona dose di ingegno.
Chi sa risolvere il trucchetto?
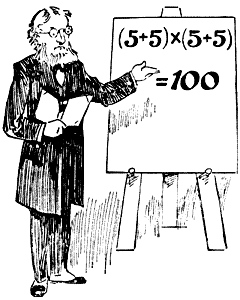
Il problema è tratto da Henry Ernest Dudeney, Amusements in Mathematics , 1917.
Potete usare tutte le operazioni aritmetiche, le parentesi e il punto decimale.
Suggerimento: H. E. Dudeney (1857-1930) era inglese e nel mondo anglosassone si usa una certa convenzione con il punto decimale...
(inserirò la soluzione il 30/01/2013)
24 gennaio 2013 - GEOMETRIA
C'era un piccolo lago, attorno al quale quattro uomini poveri avevano costruito le loro casette. Poi arrivarono quattro uomini ricchi che costruirono le loro ville, come mostrato nella figura qui sotto.
Gli uomini ricchi volevano avere il lago tutto per sé, e incaricarono un costruttore di fabbricare un muro che escludesse le casette ma lasciasse a loro il libero accesso al lago.
Poiché i quattro uomini ricchi erano anche avari, chiesero che il muro fosse il più corto possibile.
Come dovrebbe essere costruito tale muro?
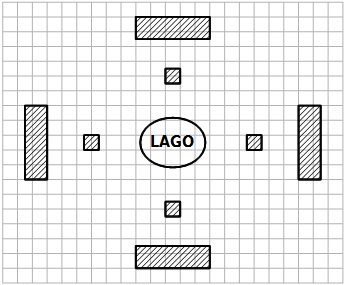
Alcuni piccoli chiarimenti:
Il problema è tratto da Henry Ernest Dudeney, Amusements in Mathematics , 1917.
(inserirò la soluzione il 30/01/2013)
20 gennaio 2013 - NOTIZIE
Più di 100 società scientifiche, università, istituti di ricerca e organizzazioni di tutto il mondo si sono uniti per dedicare il 2013 alla Matematica del Pianeta Terra .
Ne è nato il progetto Mathematics of Planet Earth 2013 che ha gli obiettivi di:
Il progetto MPE2013 è stato proposto dall’ International Mathematical Union (IMU) e ha ricevuto il patrocinio dell’ Unesco, l’Organizzazione delle Nazioni Unite per l’Educazione, la Scienza e la Cultura.
Facciamo un grande applauso a questa iniziativa e impegnamoci a dare il nostro piccolo contributo!
Nel frattempo tenete d'occhio il Daily Blog di MPE2013.
18 gennaio 2013 - LOGICA
Questo è un vecchio problema logico. Lo ripropongo come introduzione a un altro problema più difficile: Three gods: The hardest logic puzzle ever ( L'indovinello più difficile del mondo ), pubblicato da George Boolos nel 1996 su The Harvard review of philosophy . Anche quest'ultimo problema è ormai un classico, ma ci sono delle novità segnalate nelle Math News di Umberto Cerruti.
Procediamo per gradi.
---
Stai cercando la strada per il Paradiso e giungi a un bivio.
Sei certo che una delle due strade porta al Paradiso mentre l'altra porta all'Inferno. Ma non c'è nessun cartello indicatore perciò non sai da che parte andare.
Il bivio è sorvegliato da due guardiani. Uno di essi risponde sempre in modo veritiero alle domande che gli sono rivolte e l'altro mente sempre. Purtroppo tu non hai la minima idea di quale sia il guardiano sincero e quale il bugiardo.
Invece i due guardiani si conoscono bene e sanno chi è il SINCERO e chi è il BUGIARDO.
Ti è concesso di rivolgere una sola domanda a uno solo dei guardiani.
Come puoi individuare la strada per il Paradiso?
---
E' chiaro che non puoi chiedere semplicemente: "Qual è la strada per il Paradiso?" oppure oppure, indicando una delle due strade, "E' questa la strada per il Paradiso?". Non sapresti se la risposta è vera o falsa.
Devi invece porre una domanda più raffinata. Quale?
10 gennaio 2013 - PROBABILITA'
Prendo lo spunto da un problema inviato al Forum da Stefano per proporre una famiglia di problemi di probabilità.
1. Lanciando una moneta (Testa/Croce) 5 volte, qual è la probabilità che escano esattamente 3 Teste?
2. Lanciando una moneta (Testa/Croce) n volte, qual è la probabilità che escano esattamente q Teste?
3. Lanciando un dado n volte, qual è la probabilità che esca esattamente q volte il numero 6?
Ho colto l'occasione per aggiornare la Mini-teoria della probabilità (classica).
3 gennaio 2013 - ARITMETICA
Potete usare solo le seguenti cifre, tutte, in qualunque ordine, ciascuna una volta sola:
e i seguenti simboli matematici, se necessario ripetuti più volte:
------
Definizione di fattoriale doppio:
n!! = n(n-2)(n-4)... da cui, se n è pari, n!! è uguale al prodotto di tutti i numeri pari da n a 2, mentre se n è dispari, n!! è uguale al prodotto di tutti i numeri dispari da n a 1.
Esempi:
5!! = 5×3×1 = 15;
6!! = 6×4×2 = 48;
0!! = 1.
Per approfondire: http://mathworld.wolfram.com/DoubleFactorial.html
------
Il compito è quello di scrivere espressioni aritmetiche che diano come risultato tutti i numeri interi da 0 a 100.
E' meglio se i numeri compaiono nell'ordine 2, 0, 1, 3.
Tratto da: Math Forum - Manipulative 2013.
------
Esempi:
(2+1)×3+0=9
20+13=33
0.(3)×12=4
.3×120=36
------
Soluzioni
Grazie a Simone Spotti [s], Panurgo [p], Info [i], gfbo [g], Pasquale [q], Pietro [t], Diego B. [d], Alessandro B. [a], ...
Se avete trovato una soluzione, da 0 a 100, potete inviarla al Forum di BASE Cinque, dove ho postato questo problema (bisogna iscriversi). Oppure inviarmi un e-mail all'indirizzo gfbo@libero.it .
L'unico numero che resiste ancora è l'88.
Ultime notizie: l'88 ha ceduto il 12 gennaio 2013.
0 = 2+0+1-3 [g]
1 = -2^0-1+3 [g]
2 = 2×0-1+3 [g]
3 = 2^0-1+3 [g]
4 = 2+0-1+3 = 3!÷2+1-0 [d][s]
5 = 2+0^1+3 = 3!-1+0^2 [g][s]
6 = 2+0+1+3 = 2×3+0^1 [d][s]
7 = 20-13 = 2×3+0+1 [g][s]
8 = (2+0×1)^3 = 3^2-1+0 [d][s]
9 = (2+0+1)×3 = 3^2+0^1 [d][s]
10 = 2+0+(1+3)!! = 3^2+1-0 [d][s]
...
88 = 30÷√(.(1))-2 [a]
...
100 = 20×(-1+3!) = .(1)×(3!)!+20 [g][q]
.
Data creazione: settembre 2013
Ultimo aggiornamento: dicembre 2013
html 4.01 strict
Sito Web realizzato da Gianfranco Bo
