22 dicembre 2012 - NOTTURNO[BASE Cinque - Appunti di Matematica ricreativa]
22 dicembre 2012 - NOTTURNO
Dal Notturno vi propongo una scelta di irresistibili di Natale.
Stillenacht 1 (classica) - Stillenacht 2 (classica) - Stillenacht 3 (fantasia piano)
Stillenacht 4 (pastorale) - Stillenacht 5 (jazz) - Stillenacht 6 (piano jazz)
Jingle Bells 1 (jazz) - Jingle Bells 2 (violini) - Jingle Bells 3 (banjo)
Jingle Bells 4 (stride piano) - Alleluia (gospel orchestra) - Adeste fideles (orchestra)
Ave Maria (orchestra) - Bianco Natale 1 (stride piano) - Bianco Natale 2 (orchestra)
Bianco Natale 3 (swing) - Bianco Natale 4 (orchestra) - Bianco Natale 5 (piano)
Gloria (orchestra) - Greensleeves (percussioni) - Happy Christmas (John Lennon)
Happy Christmas2 (John Lennon) - Oh Tannenbaum (originale)
Oh Tannenbaum (piano jazz) - Tu scendi dalle stelle (classica)
We shall overcome (piano) - Oh happy day (orchestra, Edwin Hawkins)
When the saints go marching in (banjo)
18 dicembre 2012 - ARITMETICA - SCUOLA
La regola matematica dei paraurti
Complimenti agli alunni della scuola primaria "G. Rosa" di Bergamo per un interessante lavoro sul problema dei paraurti tratto dal Test di Bertoldino 2010 (PDF).
Ecco il testo del problema.
In un tamponamento a catena, per fortuna non grave, sono coinvolte 10 automobili. Quanti sono i paraurti danneggiati?
Gli alunni hanno generalizzato il problema trovando ben tre formule equivalenti per calcolare il numero p dei paraurti danneggiati in funzione del numero a di automobili coinvolte nel tamponamento.
I risultati del loro lavoro si trovano nella pagina intitolata La regola matematica del paraurti.
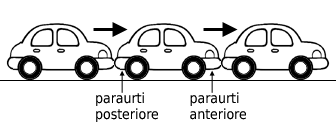
Tamponamento a catena di 3 automobili.
14 dicembre 2012 - GEOMETRIA
Origami allo START di Bologna
Il secondo tema matematico che ho incontrato a Bologna è la mostra "Un mondo di carta" organizzata dallo START - Laboratorio di Culture Creative, Bologna, Piazza Re Enzo Voltone del Podestà, tel. 051.0251008. Sito web: http://www.startlab.org/.
Ho potuto ammirare (anche se avevo poco tempo a disposizione) i lavori di origamisti di fama nazionale e internazionale tra cui il designer Ramin Razani. Oltre agli origami, c'erano oggetti di ingegneria della carta (paper engineering), che sono figure a tre dimensioni ottenute tagliando e piegando opportunamente un foglio di carta.
Ogni origami, persino un fiore o la sagoma di Batman contiene molta matematica ma con l'origami si può fare di più: si possono rappresentare veri e propri oggetti matematici come i poliedri regolari, il soma cube e l'incredibile cubo di Yoshimoto.
START, Bologna, Un mondo di carta. Origami del cubo e del dodecaedro in quattro diverse versioni.
START, Bologna, Un mondo di carta. Riconoscete, fra questi origami, il soma cube e il cubo di Yoshimoto?
START, Bologna, Un mondo di carta. Un esempio di paper engineering.
Fino a domenica 22 dicembre 2012, il sabato e la domenica alle ore 17:00 si svolgeranno visite guidate alla mostra "Un mondo di carta" e laboratori sull'arte degli origami.
La mostra è visitabile liberamente anche dal martedì al venerdì, dalle ore 9:00 alle 13:00 e dalle ore 15:00 alle 18:30, con accesso gratuito.
I visitatori potranno assistere ad una inusuale sfilata di abiti-origami, lampadari, fiori, farfalle, partecipazioni di nozze, scatole, centrotavola, quadri, insetti, giochi, cornici e un grande castello di carta!
12 12 12 ore 12:12 - GEOMETRIA
Bologna allo specchio
Ho passato due bellissime giornate a Bologna, una di neve e una di sole. Con la mia macchinetta fotografica ho esercitato un po' di arte lomografica su due temi matematici: gli specchi curvi e l'origami.
Qui vi propongo alcune immagini sugli specchi curvi.
Bologna - Piazza del Nettuno riflessa in una grande palla di Natale.
Bologna - In un bar, tazzina di caffè riflessa in un barattolo cilindrico.
Bologna, Pinacoteca Nazionale, Prospero Fontana, sepoltura di Gesù Cristo, piatto riflesso in una brocca (particolare in basso a destra).
P.S. La regola fondamentale della lomografia è: "non pensare, scatta!"
28 novembre 2012 - GEOMETRIA
Grazie a Giacomo A. che mi ha portato questo classico puzzle acquistato a un mercatino dell'artigianato.
Bisogna riuscire a far entrare quattro sagome a forma di T in un quadrato che sembra davvero troppo piccolo. Come fare?
I pezzi sono costruiti con compensato di pioppo e un listellino di faggio.
Il puzzle misura circa 12x12 cm. La precisione con cui sono tagliati i pezzi lascia a desiderare, ma si vede che il gioco è stato costruito con il cuore!
25 novembre 2012 - IL LATO POETICO
Omaggio a Giovanni Filocamo (PDF)
Giovanni Filocamo, durante il Festival della Scienza del 2012, è stato nominato, da parte di Telecom, uno dei 10 migliori ricercatori d’Italia entrando così nel gruppo Italiax10.
La "fototessera" di Giovanni si trova già da tempo nella Galleria di ritratti di BASE Cinque e due suoi libri di matematica sono segnalati nella Biblioteca del sito: Il mistero del più e Il matematico curioso.
Colgo l'occasione per pubblicare un simpatico omaggio poetico a Giovanni scritto da Gisella Malagodi, Ivana Niccolai e Grazia Raffa.
24 novembre 2012 - GEOMETRIA SOLIDA
Gli sviluppi del cubo (3 - aggiornato)
Grazie a Dana R. e a Victor G. per due preziosissime opere di carta interattiva con le quali mostrano gli 11 sviluppi del cubo in azione.
Per realizzarle hanno usato due fogli di cartoncino di colori diversi (giallo, verde) e la scheda con Gli 11 sviluppi del cubo (PDF).
22 novembre 2012 - GEOMETRIA - COMBINATORIA
Gli sviluppi del cubo (2 - aggiornato)
Ho inserito due schede sugli sviluppi del cubo in formato pdf pronte per l'uso in classe.
Scarica le schede I 35 esamini distinti e Gli 11 sviluppi del cubo.
16 novembre 2012 - GEOMETRIA - COMBINATORIA
Un esamino è un poligono formato da 6 quadrati uguali. Ogni quadrato ha almeno un lato in comune con almeno un altro quadrato.
Quanti sono i possibili esamini distinti? Se consideriamo non distinte due forme ottenute per rotazione o riflessione, gli esamini distinti sono 35. In inglese si chiamano free hexominos.
Fra i 35 esamini liberi, quanti sono sviluppi del cubo sul piano?
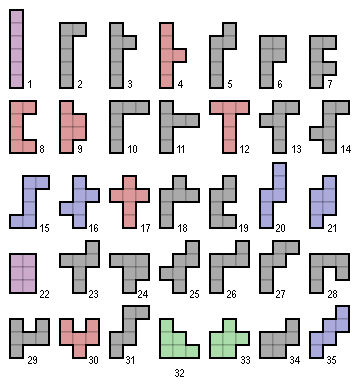
I 35 esamini liberi - Credit: Wikimedia Commons
9 novembre 2012 - ARITMETICA
L'essenza della matematica
Ricevo e pubblico con piacere l'articolo di Ivana Niccolai intitolato DISCUTENDO TRA COLLEGHI E AMICI SULLA NON ESISTENZA DELLA COSIDDETTA proprietà dissociativa IN ARITMETICA E IN ALGEBRA (PDF).
Lo spunto è la proprietà dissociativa ma il senso profondo dell'articolo riguarda l'essenza della matematica che è la libertà, come disse Georg Cantor e come noi, ogni giorno, siamo impegnati a realizzare.
L'articolo è pubblicato anche su Maecla.it e su Pintadera.
credit: Bill Watterson
7 novembre 2012 - SCIENZE
Il presidente degli Stati Uniti
Colgo l'occasione per aggiornare la pagine delle after images, un tipo particolare di illusione ottica. Ne ho parlato in queste pagine: Un signore con la barba, Jesus!, Illusioni ottiche sulle after-images.
Fissate per circa 20 secondi la crocetta che si trova sulla punta del naso della figura qui sotto. Spostate poi gli occhi sulla parete bianca di fronte a voi. Sbattete un po' le palpebre. Che cosa vedete? Dovreste vedere una persona molto importante.
L'illusione funziona bene anche con la figura stampata su carta bianca. Le dimensioni devono essere circa 9x10,5 cm.
6 novembre 2012 - SCIENZE
Simulatore di onde (javascript)
Ho preparato un simulatore di onde che funziona con il mouse (e anche con il dito per chi ama gli schermi touch e le LIM). Può essere utile per capire la differenza fra onde trasversali e onde longitudinali.
5 novembre 2012 - GEOMETRIA - SCUOLA
Il T-puzzle (aggiornato)
Ho inserito una scheda sul T-puzzle in formato pdf pronta per l'uso in classe.
Scarica il T-puzzle.pdf.
1 novembre 2012 - GEOMETRIA - ARITMETICA
Il calibro aureo (aggiornato)
Come usare il calibro aureo per cercare proporzioni auree nel nostro corpo.
29 ottobre 2012 - GEOMETRIA - ARITMETICA
Il calibro aureo è uno strumento utilissimo per cercare proporzioni auree nel nostro corpo e nella natura intorno a noi.
Riporto qui sotto le istruzioni minime per costruirne uno.
Io ho usato un'assicella di ramino di 10x5 mm lunga 2 m. Vi serviranno inoltre quattro bulloni 18x3 mm con relativi dadi e due rondelle.
AE=AG=340 mm
BF=210 mm
CE=130 mm
AB=AC=BD=CD=130 mm
Attenzione! Le misure indicano le distanze tra due fori o tra un foro e una punta. Le assicelle devono essere un po' più lunghe, ovviamente.
In internet si trovano alcune varianti di questo strumento, basta cercare con la chiave "golden section gauge".
25 ottobre 2012 - GEOMETRIA
Quattro triangoli con sei stecchini
Hai a disposizione 6 stecchini con i quali devi costruire 4 triangoli equilateri uguali. Come fai?
E' un quesito fondamentale che ogni tanto ritorna su BASE Cinque.
Lo trovate per esempio nella pagina dedicata a Albert Einstein e la quarta dimensione, nella pagina dei Consigli per vincere le sfide logico-matematiche e nei Quesiti più famosi.
Proprio in questi giorni ho ricevuto una nuova soluzione da Filippo Z., alunno di una scuola primaria di Bergamo. Un applauso a Filippo!
22 ottobre 2012 - SCUOLA - ARITMETICA
Ore di lezione e ore di lavoro degli insegnanti (aggiornato)
Oggi mi è caduto l'altro occhio su un grafico pubblicato dal quotidiano "IL SECOLO XIX". Così, direi che va molto meglio: si possono confrontare dati omogenei.
L'oculista mi ha consigliato di non farmi più cadere gli occhi su certi grafici, per almeno un anno. Promesso.
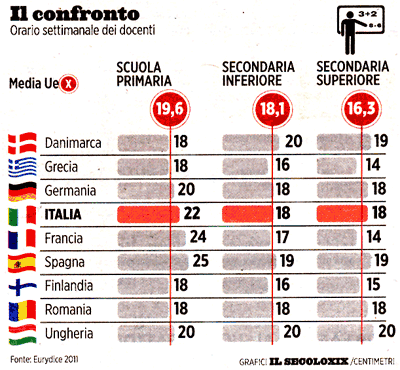
credit: http://www.ilsecoloxix.it/
21 ottobre 2012 - SCUOLA - ARITMETICA
Ore di lezione e ore di lavoro degli insegnanti
Il ministro dell'Istruzione Francesco Profumo ha proposto di aumentare le ore settimanali di lezione degli insegnanti, portandole da 18 a 24. Gratis. Così facciamo un favore all'Italia e ci allineiamo con l'Europa.
BASE Cinque è un sito di matematica e non voglio andare fuori tema. Perciò vi propongo soltanto un piccolo esercizio di matematica.
Alcuni giorni fa mi è caduto l'occhio sul grafico riprodotto qui sotto, pubblicato sul quotidiano "la Repubblica".
Ho recuperato l'occhio che mi ha portato due domande.
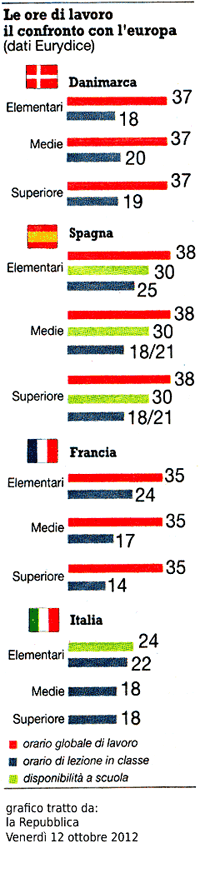
credit: http://www.repubblica.it/
18 ottobre 2012 - ARITMETICA - SCUOLA
Ma... la proprietà dissociat*va esiste o non esiste?
credit: Bill Watterson
Cari colleghi, nel glorioso libro di Aritmetica che usavo alle medie nel 1963, e in alcuni libri di scuola che si usano ancora oggi, si trova una regola di calcolo chiamata "Proprietà diss*ciat*va dell'addizione", enunciata più o meno così:
Se in una addizione si sostituisce un addendo con due addendi la cui somma è uguale all'addendo sostituito, il risultato non cambia.
Seguono esempi del tipo:
7+8 = 7+(3+5) = 7+3+5 = (7+3)+5 = 10+5 = 15
O anche:
45+23 = 40+5+20+3 = 40+20+5+3 = 60+8 = 68
Attenzione: questa possibilità di sostituire gli addendi non è una proprietà dell'addizione ma soltanto una strategia utile per eseguire calcoli mentali e per applicare il classico algoritmo dell'addizione.
La proprietà di*s*ciat*va dell'addizione non esiste! Tranquilli, si vive benissimo anche senza.
Due classiche proprietà dell'addizione sono la p. commutativa e la p. associativa.
Vi chiederete: perché c'è un'invasione di asterischi nella parola "di*s*c*at*va?
Primo per non farla trovare dai motori di ricerca, secondo per invitare tutti a far sparire completamente questa evanescente proprietà d*s*o*i*t*v*. O no?
15 ottobre 2012 - GEOMETRIA - SCUOLA
Dedicato al quadrato (aggiornato)
Aggiornata la pagina del quadrato con un nuovo quesito ispirato da MAAMinuteMath.
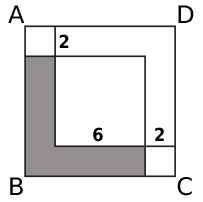
Area della L
Il quadrilatero ABCD è un quadrato. Dentro questo quadrato sono disegnati altri tre quadrati i cui lati misurano, in centimetri, come indicato nella figura.
Qual è l'area del poligono colorato di grigio?
11 ottobre 2012 - GEOMETRIA - SCUOLA
Mettiamo per un momento da parte i soliti problemi di geometria che si fanno a scuola e cominciamo a osservare il quadrato (e altre figure geometriche) sotto diversi punti di vista. Facciamo in modo che esso diventi un nostro amico personale.
Vi propongo, in questa pagina, alcuni quesiti interessanti, tutti basati su un quadrilatero molto particolare: il quadrato.
Ecco due esempi.
Quanti quadrati?
Nella seguente griglia 5x5 si possono distinguere vari quadrati di
dimensioni che vanno da 1x1 a 5x5.
Quanti di questi quadrati contengono il cerchio nero che si trova al centro
della griglia?
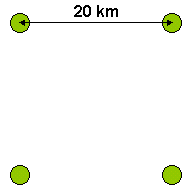
La rete stradale ottima
Quattro paesi sono situati in una grande pianura, ai vertici di un quadrato
di lato 20 km.
L'obiettivo è quello di costruire la rete stradale più corta possibile che
metta in comunicazione ciascun paese con gli altri tre.
Lo spunto mi è venuto dalla rubrica "Il matematico impertinente" di Piergiorgio Odifreddi sulla rivista Le Scienze n. 530 di ottobre 2012. Partendo dalle proprietà di due semplici figure, il quadrato e il pentagono, Odifreddi ci guida in un affascinante percorso che va dai numeri irrazionali alle geometrie finite passando per i grafi euleriani.
6 ottobre 2012 - LIBRI
L'ultimo teorema di Fermat in chiave fantascientifica
Arthur C. Clarke, Frederick Pohl, L'ultimo teorema, traduzione di Flora Staglianò, A. Mondadori, Collana Urania, 2012.
Il romanzo è ambientato nello Sri Lanka, più o meno ai giorni nostri, e racconta due storie parallele.
La storia principale segue la vita di un giovanissimo genio della matematica, Ranjit Subramanian. Durante gli studi presso l'Università di Colombo, Ranjit si appassiona all'ultimo teorema di Fermat, che egli vorrebbe dimostrare con le tecniche disponibili ai tempi del grande matematico francese, vissuto nel 1600.
La storia parallela è ambientata in un luogo lontanissimo dove i Grandi Galattici rilevano segnali provenienti da esplosioni di bombe nucleari sulla Terra. I Grandi Galattici inviano ai terrestri il messaggio "cessare e desistere". Poiché tale messaggio non ha alcun effetto, essi lanciano una flotta sulla Terra per sterminare la specie umana.
Tranquilli, sopravviveremo...
Ho trovato interessante la parte del romanzo dedicata alla matematica perché riesce a essere avventurosa e nello stesso tempo non approssimativa.
Per esempio, già nelle prime pagine c'è un riferimento al calcolo delle radici con l'uso del famoso triangolo numerico che è detto in Francia - di Pascal, in Italia - di Tartaglia, in Iran - di Khayyam, in Cina - di Yang Hui.
2 ottobre 2012 - GEOMETRIA
La stella nascosta (aggiornato)
Ho aggiornato la pagina della stella nascosta di Samuel Loyd con un nuovo problema leggermente più difficile.
In questa immagine c'è una stella a cinque punte (quasi) perfettamente simmetrica. Siete capaci di trovarla?
29 settembre 2012 - MISURE
I pollici quadrati colpiscono ancora
---
Domanda: se un pollice è lungo (circa) 2,5 cm allora un pollice quadrato equivale a quanti centimetri quadrati?
---
Faccio scherzosamente questa domanda perché giovedì 27 settembre al programma televisivo "L'eredità" ho sentito una frase del tipo: "Sull'interruttore della luce ci sono ...(un certo numero)... di batteri per ogni 2,5 cm2."
Ecco, quel 2,5 cm2 mi suona strano. Probabilmente hanno preso il dato da un sito inglese dove si usano ancora le misure imperiali e le densità di batteri sono date in unità per pollice quadrato (square inch).
Il gioco in questione era "La scossa" e la domanda riguardava la classifica delle cose più infette che tocchiamo ogni giorno.
A titolo di curiosità e senza conferme scientifiche, riporto "The Dirtiest Things You Touch Every Day" tratta dal sito http://www.ranker.com
1. Banconote
2. Interruttore della luce
3. Tastiera del computer
4. Schermo touch del telefonino
5. Sedile del vaso sanitario (water)
6. Carrello della spesa
7. Telecomando del televisore
8. Vasca da bagno
9. Lavandino della cucina
10. Spugna da cucina
11. Maniglia della porta
12. Maniglia del frigorifero
13. Manopola del cambio dell'automobile
---
Risposta alla domanda iniziale:
1 pollice quadrato = (2,5)2 cm2 = 6,25 cm2.
---
25 settembre 2012 - LABMAT
Come costruire un Teorema di Pitagora portatile utilizzando fogli di policarbonato alveolare di tre colori diversi (si trovano nei negozi di bricolage).
21 settembre 2012 - DAL FORUM
Un minuto di matematica al giorno
Franco segnala MAAMinuteMath, un blog della Mathematical Association of America. Ogni giorno viene presentato un piccolo problema per tenere in esercizio la mente (e per noi anche l'inglese).
Gli esercizi sono adatti a ragazzi dell'8°, 10° e 12° grado, che da noi corrispondono alla 3° media, 2° e 4° superiore.
19 settembre 2012 - DAL FORUM
Geogebra per iPad
Simona Riva segnala che il team di GeoGebra ha deciso di creare un'app per iPad, anch'essa gratuita, e sta raccogliendo fondi per sveltire la fase di programmazione. Se volete contribuire potete donare qui: GeoGebra for the iPad.
16 settembre 2012 - TEORIA DEI GIOCHI
Il dilemma del prigioniero (e l'assioma di razionalità)
Aldo e Baldo sono sospettati di aver commesso una rapina insieme.
La polizia li arresta entrambi e li chiude in due celle separate, in modo che non possano comunicare.
Il giudice non ha prove sufficienti per poterli condannare, perciò offre a ciascuno di loro un accordo. Le regole dell'accordo sono le seguenti:
Qual è la migliore strategia per ciascuno di essi: confessare o non confessare?
credit: Poojadfp's Blog
Per risolvere il dilemma è utile conoscere l'assioma di razionalità che è alla base della teoria dei giochi.
Assioma di razionalità. Nessun giocatore sceglierebbe mai una strategia se ne ha a disposizione un’altra che gli permette di ottenere risultati migliori, qualunque sia il comportamento dell’avversario.
10 settembre 2012 - IL LATO COMICO
Spending review a scuola
Parola d'ordine: bando alla carta! Tutti i servizi on-line!
Non preoccupatevi.
Sarà più facile di quanto sembra.
Nota. Spending review è il nome amichevole con cui si chiama la LEGGE 7 agosto 2012, n. 135 (PDF), recante disposizioni urgenti per la revisione della spesa pubblica con invarianza dei servizi ai cittadini, in vigore dal 15 agosto 2012.
Sembra fuori tema ma non lo è: c'è molta matematica!
8 settembre 2012 - SCUOLA
La matematica nelle <nuove> Indicazioni Nazionali del 27 luglio 2012
Il MIUR (Ministero dell'Istruzione, dell'Università e della Ricerca) ha pubblicato, il 27 luglio 2012, una nuova versione delle Indicazioni nazionali per il curricolo della scuola dell’infanzia e del primo ciclo d’istruzione.
In queste Indicazioni c'é scritto cosa devono imparare i nostri ragazzi nella scuola elementare e media, senza trascurare l'asilo.
Cosa c'è di nuovo in matematica?
5 settembre 2012 - LIBRI
Ritorna in edicola "il MONDO è MATEMATICO", una collezione di 40 libri pubblicata dalla RBA Italia (mondomatematico).
La prima uscita è La sezione aurea. Il linguaggio matematico della bellezza, di Fernando Corbalàn.
I libri escono in edicola il giovedì di ogni settimana. Non sono rilegati ma hanno una robusta copertina di cartone e costano 9,99 EUR.
Alcuni titoli interessanti:
02. Matematici, spie e pirati informatici. Decodifica e crittografia
03. I numeri primi. Un lungo cammino verso l’infinito
07. I segreti del Pi greco. Perché è impossibile la quadratura del cerchio?
08. Dilemma del Prigioniero e strategie dominanti. La strategia dei giochi
11. Mappe del metrò e reti neurali. La teoria dei grafi
12. L’armonia è questione di numeri. Musica e matematica
16. L’inganno dell’occhio. L’arte vista con occhi matematici
17. Dall’altra parte dello specchio. Le simmetrie in matematica
23. Le mille sfaccettature della bellezza geometrica. I poliedri
32. La farfalla e il ciclone. La teoria del caos e i cambiamenti climatici
34. L’arte di contare. Calcolo combinatorio ed enumerazione
36. Forme che si deformano. La topologia
37. Donne della matematica. Da Ipazia a Emmy Noether
40. Pianeta matematico. Un viaggio numerico attorno al mondo
Nell'edizione spagnola i nomi degli autori sono scritti in copertina mentre nell'edizione italiana bisogna andarli a cercare nel colophon. Chissà perché.
3 settembre 2012 - IL LATO COMICO
Aggiornata la pagina umoristica dedicata alla personalità del matematico con la barzelletta n. 29.
29. Come pensa un logico-matematico
Mia moglie mi ha detto: "Vai nel negozio e compra un cartone di latte e, se hanno delle uova, comprane sei."
Sono tornato a casa con sei cartoni di latte.
Mia moglie mi ha chiesto: "Perché diavolo hai comprato sei cartoni di latte?"
"Perché avevano delle uova."
...
Dove ho sbagliato?
1 settembre 2012 - LIBRI
Il miglior libro che ho letto quest'estate:
Roberto Lucchetti, Giuseppe Rosolini, Matematica al bar. Conversazioni su giochi, logica e altro, Franco Angeli, Milano, 2012.
Matematica al bar, particolare della copertina
In breve. E' un libro appassionante di vera matematica. Ogni volta che arrivi in fondo a una pagina devi voltarla per vedere come la storia va avanti. La prima metà del libro è un'ottima introduzione alla teoria dei giochi, compresi i giochi non cooperativi studiati dal mitico John Forbes Nash. La seconda metà tratta prevalentemente argomenti di logica matematica.
Complimenti a Géraldine D'Alessandris per i bellissimi ritratti dei matematici (e di alcuni campioni sportivi) disegnati a penna.
La gallina leggera... e
intelligente (aggiornato con soluzione)
Blog Invito alla natura
Segnalo il blog Invito alla natura al quale collaboro dal 1 maggio 2012. E' dedicato alla didattica delle scienze nella scuola secondaria di primo grado (media) ma gli articoli contengono spesso anche un pizzico di matematica.
Cari amici di BASE Cinque e cari colleghi insegnanti di matematica, fra pochi giorni inizierà la scuola e vorrei augurarvi buon lavoro con un po' di umorismo edificante. La parabola che sto per raccontarvi si ispira a un esperimento scientifico veramente realizzato tanti anni fa.
Un ricercatore chiuse 5 scimmie in una stanza dove si trovava una scala e in cima alla scala c'erano delle banane.
Una delle scimmie salì sulla scala per prendere le banane ma...
Relax on a rainbow, di Ellis Nadler (su toonpool)
credit: Auke van der Weide
La gallina leggera... e intelligente
La gallina Camilla deve attraversare un ponte sospeso.
Un cartello all'inizio del ponte avverte che, per non essere portati via dal forte vento che attraversa il ponte, è necessario pesare almeno 5450 g (grammi).
Purtroppo l'ago della bilancia su cui Camilla si pesa, si ferma su 5414 g!
Per fortuna, proprio all'ingresso del ponte, c'è un addetto comunale che vende sassi del peso di 10 g al prezzo di 1 cent il grammo.
La gallina possiede soltanto una moneta da 2 Euro.
Quanto denaro rimarrà in tasca a Camilla quando il suo peso, sassi compresi, le permetterà di attraversare il ponte?
---
(La versione originale è tratta da http://www-dimat.unipv.it/PorteAperte/quiz.html, una pagina di curiosità matematiche del Dipartimento di Matematica "Felice Casorati", Università di Pavia. Il problema si intitola: "Un quiz... trabocchetto".)
---
Riporto qui di seguito i pesi delle monete. Vi saranno utili per risolvere il problema.
| Moneta | Peso
(grammi) |
| 1 cent | 2,30 |
| 2 cent | 3,06 |
| 5 cent | 3,92 |
| 10 cent | 4,10 |
| 20 cent | 5,74 |
| 50 cent | 7,80 |
| 1 EUR | 7,50 |
| 2 EUR | 8,50 |
Come si chiama il capotreno?
(aggiornato con risposte)
Bianchi, Neri, Rossi, capotreno e macchinista... che gioco di logica è?
Esistono diverse varianti di un problema di logica con questi personaggi. Qui riporto una versione, non facilissima, che ho trovato nel libro di Irving M. Copi, Introduzione alla logica, Il Mulino, Bologna, 1964.
Bianchi, Neri e Rossi sono il capotreno, il macchinista e il controllore di un treno, ma non sono elencati nell’ordine esatto. Sullo stesso treno ci sono tre passeggeri con gli stessi tre nomi, il sig. Bianchi, il sig, Neri e il sig. Rossi.
Si hanno le seguenti informazioni:
Come si chiama il capotreno?
Osservate
l'immagine qui sotto e cercate di scoprire cosa ha di speciale.
Questo modo di scrivere i numeri ha delle applicazioni scientifiche interessanti.
Vi invito a una WebQuest (caccia al tesoro nella rete) per scoprire chi l'ha inventato e a cosa può servire.
La prima traccia sono le Math News del prof. Umberto Cerruti.
Questa notizia è recente ma non è facilissimo trovarla, bisogna rovistare un po'...
Ho fatto la stessa proposta anche al Forum!
Che cosa è la spirale di Teodoro di
Cirene?
BASE Cinque ha un motore di ricerca interno basato sul servizio FreeFind. Ogni settimana FreeFind mi invia un rapporto sulle ricerche fatte dai lettori.
Purtroppo, in molti casi, le parole cercate non si trovano sul sito. Questo mi dispiace, ma mi dà anche l'opportunità di affrontare nuovi argomenti.
Perciò, ogni tanto dedicherò una pagina a una domanda particolarmente interessante (e per me accessibile).
Nel frattempo, invito tutti a partecipare al Forum!
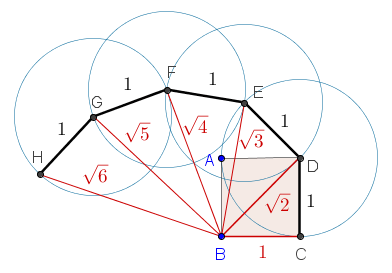
La spirale di Teodoro è una costruzione geometrica che permette di ottenere le radici quadrate di tutti i numeri interi. (grazie Geogebra)
Avete il senso del numero?
Volete valutare la vostra abilità di contare a colpo d'occhio (Approximate Number System aptitude)? Visitate il sito Panamath (http://www.panamath.org/index.php) e partecipate a una ricerca scientifica che ha già coinvolto più di 100.000 persone nel mondo. Entrate nella pagina Test Yourself e seguite le istruzioni.
Niente paura, il test è semplicissimo! Dovete solo decidere se i pallini gialli sono più o meno numerosi di quelli blu, in varie situazioni.
Alcune indicazioni da parte mia:
Alla fine otterrete una valutazione scientifica e molto dettagliata del vostro senso innato del numero.
Risposte ai problemi di Giugno
Quante vocali ha la risposta corretta di questa domanda? (Inserito nella pagina Proposizioni autoreferenziali - aggiornato)
Il problema delle due uova (aggiornato - dal Forum)
Un
problema autoreferenziale tratto dall'Olimpiade Brasiliana di
Matematica 2012, prima fase, livello 3.
Quante vocali ha la risposta corretta di questa domanda?
A) Cinque, B) Quattro, C) Tre, D) Due, E) Una
La risposta è nella pagina: Proposizioni autoreferenziali.
Il problema delle due
uova (aggiornato)
Avete due uova (di un tipo molto resistente) e potete
accedere a un palazzo di 100 piani.
Dovete progettare un metodo efficiente per stabilire da quale altezza massima,
misurata in piani, un uovo di questo tipo può cadere senza rompersi.
Sembra che questo problema sia una delle Google interview questions
(domande poste ai colloqui di lavoro presso Google).
Programmi scolastici
Pubblicata il 30 maggio 2012 la bozza dei nuovi programmi scolastici (Indicazioni nazionali per il curricolo della scuola dell'infanzia e del primo ciclo di istruzione). L'edizione precedente risale al 2007.
Bozza Indicazioni del 30 maggio 2012
La parola chiave è: competenze.
Il nostro sistema formativo si baserà su 8 competenze definite dal Parlamento Europeo nel 2006:
1) comunicazione nella madrelingua;
2) comunicazione nelle lingue straniere;
3) competenza matematica e competenze di base in scienza e tecnologia;
4) competenza digitale;
5) imparare a imparare;
6) competenze sociali e civiche;
7) spirito di iniziativa e imprenditorialità;
8) consapevolezza ed espressione culturale.
Il testo completo, breve ma esauriente, si trova nella RACCOMANDAZIONE DEL PARLAMENTO EUROPEO E DEL CONSIGLIO del 18 dicembre 2006 relativa a competenze chiave per l'apprendimento permanente.
Le scuole hanno tempo fino al 30 giugno per rispondere a un questionario del Ministero sulle nuove Indicazioni per il curricolo. Informazioni dettagliate nella pagina Consultazione 2012, a cura dell'Agenzia Nazionale per lo Sviluppo dell'Autonomia Scolastica, anche chiamata INDIRE.
Saggio delle competenze 2012: iTrivium & iQuadrivium
Coffer illusion (L'illusione
del forziere)
Sembra un quesito di geometria invece è una domanda di neuroscienze. L'autore è il prof. Anthony M. Norcia, ricercatore presso lo Smith-Kettlewell Eye Research Institute.
Quanti cerchi vedete in questa figura?
Questa illusione ottica è stata finalista al Best Illusion of the Year Contest (concorso per la miglior illusione dell'anno) nel 2006.
Vedi anche: Le facce nascoste, La stella nascosta.
Super-sintesi
delle formule sul volume e sulle aree dei solidi.
Un poster da appendere in classe per l'esame di matematica della terza
media.
Libri
aggiunti alla Biblioteca:
Gargantini Mario, Bersanelli Marco, Solo lo stupore conosce. L'avventura della ricerca scientifica, Rizzoli, (BUR, collana I libri dello spirito cristiano), 2003.
Federico Neresini, Giuseppe Pellegrini, Annuario scienza e società 2012, edizioni Il Mulino, 2012.
Aggiornata la pagina su La
piramide di Cheope.
In un
negozio di giochi intelligenti per bambini e ragazzi ho trovato un bel
cubo di Rubik 2x2x2.
In attesa di studiarlo bene, vi propongo un micro-manuale in tre passi per risolverlo.
1) Questo cubo non ha spigoli, ma soltanto angoli.
2) Il primo strato risolvetelo intuitivamente: è davvero facile!
3) Per il secondo strato, seguite il metodo del cubo 3x3x3 : ma soltanto nella parte finale, quella che spiega come mettere a posto gli angoli del terzo strato.
Aggiornata la pagina dei Pentaflores con un nuovo fiore: la
pentas.
Pentas lanceolata
Aggiornata la pagina Dissezione
del cubo in tre piramidi uguali.
Una di-mostrazione della formula del volume della piramide:
V = (Ab · h) / 3 (Area di base x altezza : 3)
Perché si divide per 3?
Aggiornata la pagina dei Pentaflores con cinque nuovi fiori a
cinque petali: il cetriolo, la primula officinale, il gelsomino, il pitosforo
e... un fiore misterioso.
Primula (officinalis?)
Premessa: questo articolo è soltanto un divertimento e nulla più.
Tutti sanno che il volto umano è pieno di elementi che stanno fra di loro in rapporto aureo. La stessa cosa avviene nel pentagono e nel decagono in cui siano tracciate le diagonali.
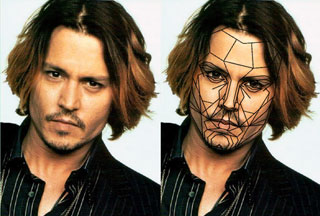
Mettendo assieme questi fatti, il dottor Stephen R. Marquardt, ha ideato una struttura geometrica che vorrebbe essere il termine di paragone per misurare la bellezza di un volto. Tale struttura è nota col nome di Golden Mask o Phi mask.
Per esempio, il volto di John Christopher Depp si adatta perfettamente alla maschera, nella variante maschile.
Usando una fotocamera digitale, un programma di disegno e uno schema della Phi Mask, chiunque può divertirsi a valutare quanto un volto si avvicina ai canoni aurei.
Un prisma è sempre un
prisma (aggiornato)
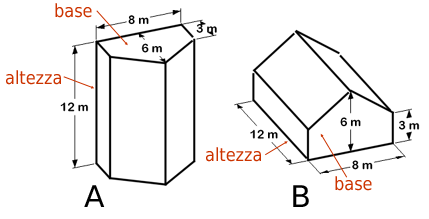
A è un prisma, di quelli che sono disegnati nei libri di scuola.
B è una serra ma è anche un prisma che ha le stesse misure di A.
La formula per calcolare il volume del prisma è:
V = Ab·h (area di base per altezza).
Se dovete calcolare il volume della serra, qual è la base e quale l'altezza?
Aggiornata la pagina Cubi di
vetro sintetico.
Uno dei nostri cubi perde irrimediabilmente acqua. Che fare?
Abbiamo sostituito l'acqua con le cosiddette "patatine" soffici ed ecologiche per imballagi.
Libro
aggiunto alla Biblioteca:
IL FIBONACCI. Breve viaggio fra curiosità matematiche. Aspetti insoliti o nascosti della matematica visti con gli occhi di Franco Conti. A cura di Edoardo Sinibaldi, Unione Matematica Italiana, 2011.
Mariti gelosi che devono attraversare
un fiume con le loro mogli
Grazie a Pietro Vitelli per la dimostrazione completa e dettagliata, con alcune parti inedite, di un classico problema di attraversamento.
Torniamo ancora una volta su un concetto fondamentale: come varia il volume di un cubo al variare del lato?
Non basta la teoria, ci vuole anche la pratica.
Il cubo di Yoshimoto
originale
Un cubo formato da otto cubi più piccoli, all'inizio è d'argento, ma poi diventa d'oro.
Poi si divide in due poliedri stellati, uno d'argento e uno d'oro.
Ciascuno di questi due poliedri si trasforma un cubo grande come il cubo iniziale.
Infine questi due cubi si incastrano l'uno nell'altro e si ritorna al punto di partenza.
Magia, arte, matematica.
Il cubo di Yoshimoto, esposto al MoMA (Museum of Modern Art di New York), ci ha affascinato e ne abbiamo comprato un esemplare!
Libro
aggiunto alla Biblioteca:
Ioannes Broscius, (Jan Brozek), De numeris perfectis disceptationes duae, 1637. (Si trova su Google Books)
Libri
aggiunti alla Biblioteca:
Carolus Bovillus (Charles de Bovelles), Liber de intellectu. Liber de sensu. Liber de nichilo. Ars oppositorum. Liber de generatione. Liber de sapiente. Liber de duodecim numeris. Epistole complures. Insuper mathematicum opus quadripartitum. Liber de numeris perfectis. Liber de mathematicis rosis. Liber de geometricis corporibus. Liber de Geometricis supplementis, 1510. (Si trovano su Google Books, in un unico volume)
Come è possibile che Charles de Bovelles, vissuto nel 1500, fosse arrivato a trovare i numeri perfetti fino a questo mostro di 19 cifre:
2 305 843 008 139 952 128
e oltre?
La risposta è semplicissima...
Ho aggiornato la
Guida per risolvere il cubo di
Rubik correggendo alcuni punti oscuri che mi sono stati segnalati
da diversi lettori. Grazie a tutti!
Il cubo di Yoshimoto
semplificato
Ancora grazie a Mihail e a un gruppo di volontari tagliatori, abbiamo migliorato il nostro cubo di Yoshimoto.
Potete scaricare il file Cubo_Yoshimoto_modello.pdf con i disegni già pronti per la stampa.
(immagine gif animata tratta e adattata da:
http://www1.ttcn.ne.jp/a-nishi/y_cube/z_y_cube.html)
Duplicazione del cubo
(corretto)
Tutti sanno che un cubo di lato 10 cm equivale a 1 litro. Ma pochi credono, anche a vederlo, che basta allungare il suo lato di 2,6 cm per raddoppiare il suo volume, cioè farlo diventare di 2 litri.
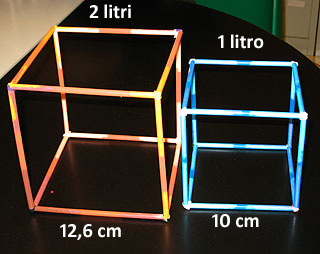
Grazie a Mihail e a Maxim per questa versione molto semplificata ma bella e istruttiva del cubo di Yoshimoto.
Libri
aggiunti alla Biblioteca:
Kurt Gödel, La prova matematica dell’esistenza di Dio, Torino, Bollati Boringhieri, 2006.
Luigi Giussani, Spirto gentil, Rizzoli, 2011.
Un invito all'ascolto della grande musica guidati da Luigi Giussani.
Amaya è tornato!
(dopo un periodo di stasi dal 2009 al 2011)
Amaya è un programma open source che serve a
costruire siti web. E' un editor visuale, cioè assomiglia a un
word processor, ma permette anche di intervenire direttamente sul
codice html, css e javascript.
Nato nel 1996, è attualmente sviluppato a cura dell'INRIA, del W3C e del WAM.
Dal centimetro cubo al decimetro cubo e altre unità di volume.
Piastrellatura di un
rettangolo
Un problema non proprio facile risolto in 14 modi diversi da Stan Wagon, nel 1987.
Stan Wagon
e la sua bicicletta con le ruote quadrate.
E' comodissima su una strada rotonda...
Pensiero laterale matematico
(2) [Aggiornato/con risposte]
Somma 15
Su un tavolo ci sono i numeri da 1 a 9.
Aldo e Baldo prendono alternativamente un numero.
Vince il primo che ha tre numeri la cui somma è 15.
Chi fa la prima mossa a questo gioco, ha una strategia di vittoria sicura?
Nota. Ogni giocatore, durante il gioco, prende più di tre numeri. Per vincere è necessario e sufficiente che fra i numeri presi ce ne siano tre la cui somma sia 15.
Pensiero laterale matematico
(2)
Soldato non guardato
Undici soldati sono disposti in un campo in modo che le distanze fra di loro, presi a due a due, siano tutte diverse.
A un certo punto il caporale (che non fa parte del gruppo) ordina: "Ciascuno di voi guardi il soldato più vicino!"
Dimostrate che almeno un soldato non è guardato da nessuno.
Il primo
libro che aggiungo alla Biblioteca nel 2012.
Alexander Abian, La teoria degli insiemi e l'aritmetica transfinita, Feltrinelli, Milano, 1972.
A un certo punto ho voluto capire veramente la teoria degli insiemi. Il matematico armeno Alexander Abian è stato l'unico che me l'ha fatta capire. Attenzione però: questo suo libro è formato da 800 pagine di matematica. Ma non è solo un elenco di definizioni, assiomi, teoremi e dimostrazioni, c'è anche spiegato perché ogni definizione, ogni assioma e ogni teorema è necessario per sviluppare teoria.
xhtml 1.1
Sito Web realizzato da Gianfranco Bo