24 dicembre
2019[BASE Cinque - Appunti di Matematica ricreativa]
24 dicembre
2019
Dal Notturno vi propongo una scelta di irresistibili di Natale (sono file MIDI).
Stillenacht 1 (classica) - Stillenacht 2 (classica) - Stillenacht 3 (fantasia piano) - Stillenacht 4 (pastorale) - Stillenacht 5 (jazz) - Stillenacht 6 (piano jazz) - Jingle Bells 1 (jazz) - Jingle Bells 2 (violini) - Jingle Bells 3 (banjo) - Jingle Bells 4 (stride piano) - Alleluia (gospel orchestra) - Adeste fideles (orchestra) - Ave Maria (orchestra) - Bianco Natale 1 (stride piano) - Bianco Natale 2 (orchestra) - Bianco Natale 3 (swing) - Bianco Natale 4 (orchestra) - Bianco Natale 5 (piano) - Gloria (orchestra) - Greensleeves (percussioni) - Greensleeves armonizzato da Giorgio Pacchioni - Happy Christmas (John Lennon) - Happy Christmas2 (John Lennon) - Oh Tannenbaum (originale) - Oh Tannenbaum (piano jazz) - Tu scendi dalle stelle (classica) - We shall overcome (piano) - Oh happy day (orchestra, Edwin Hawkins) - When the saints go marching in (banjo) - Jingle bell rock (orchestra).
15 dicembre
2019
I migliori 3+2+1 libri di matematica che ho letto nel 2019 (o leggerò presto)
Libri che mi sono regalato per Natale e che aspetto con impazienza.
Menzione onorevole.
2 dicembre
2019
Gli sviluppi del cubo [aggiornato]
Ho corretto un "bug" in questa pagina dedicata agli 11 sviluppi del cubo e colgo l'occasione per porre una nuova domanda.
Questi sono gli 11 sviluppi del cubo.
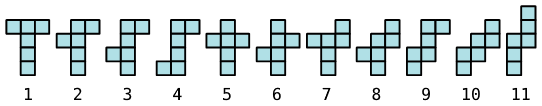
In tutto sono formati da 11×6 = 66 quadrati.
I fattori di 66 sono: 1-2-3-6-11-22-33-66.
E' possibile disporre gli 11 sviluppi del cubo in modo da formare un rettangolo, o qualche altra figura interessante?
Grazie a Sabrina C. e ai suoi alunni per la segnalazione del "bug".
15 novembre
2019
E' un teorema semplice, potente e bello a cui purtroppo si dà poca importanza a scuola. Merita una maggiore attenzione.
Allora gli dedico una pagina, prendendo spunto da un problema postato al Forum da Panurgo.
Esagono in un cerchio.
Un esagono con i lati di lunghezza 2, 7, 2, 11, 7, 11 è inscritto in un cerchio di raggio...?
24 ottobre
2019
Umorismo matematico 2019 [aggiornato]
Base 10
Questa vignetta è un piccolo test. Se la capite in 10 secondi, allora siete matematici.
Qualunque base di numerazione, scritta in quella base, è base 10.
---
Secondo un luogo comune, noi conteremmo in base 10 perché abbiamo 10 dita nelle due mani, quindi l'omino verde conterebbe in base 4 perché ha 4 dita. Ma così non è scritto bene.
25 settembre
2019
Numeri sulla lavagna
Sulla lavagna sono scritti i numeri da 1 a 10.
Scegli due numeri a caso, a, b, cancellali e scrivi sulla lavagna il numero dato dalla loro somma più il loro prodotto, cioè (a+b+ab).
Ora ci sono 9 numeri sulla lavagna.
Ripeti la procedura: scegli due numeri a caso, cancellali e scrivi il numero dato dalla loro somma più il loro prodotto.
Ora ci sono 8 numeri sulla lavagna.
Ripeti la procedura fino a quando rimane un solo numero.
Che numero è?
---
Inventa una variante di questo problema.
A me, per esempio, piace questa: al posto di a, b, scrivi √(a2+b2).
Che numero ottieni alla fine?
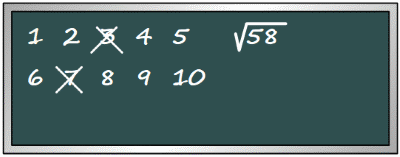
Nella figura c'è un esempio del primo passaggio
Esistono molti problemi di questo tipo nella matematica ricreativa. Sono delle piccole avventure!
12 settembre
2019
I 77 problemi per ragazzi di Vladimir Igorevic Arnold
Cari amici, vi segnalo un prezioso libretto del grande matematico russo Vladimir Igorevic Arnold (1934-2010) intitolato Problemi per ragazzini dai 5 ai 15 anni.
Il libretto contiene 77 problemi utili a sviluppare la capacità di ragionare, scelti o composti dall'autore.
La maggior parte di essi non richiede conoscenze particolari al di là della matematica di base. Tuttavia, risolverne alcuni può essere una sfida anche per i professori.
Potete scaricare liberamente il libretto (PDF) in traduzione italiana dal sito IMAGINARY – open mathematics, a questo link:
Credit foto: Oberwolfach Photo Collection
10 settembre
2019
33 problemi di matematica ricreativa
Cari colleghi insegnanti di matematica, genitori, studenti, ho preparato un libretto con 33 problemi tratti da questo sito, BASE Cinque.
Lo potete scaricare in versione sia PDF sia ODT. E' in formato A5.
Il file ODT (Open Document Text) si può aprire e modificare con Open Office Write, Libre Office Write o WinWord.
Potete quindi modificare i problemi adattandoli alle esigenze delle vostre classi.
Ho sperimentato tutti i problemi nella scuola media.
Tuttavia questi esercizi di matematica ricreativa si possono affrontare a vari livelli, dalla scuola di base all'università. Dipende da come li presentate.
Buon divertimento!
Ah, la figura della copertina significa che TUTTI possono arrivare alla matematica, ciascuno secondo il proprio percorso, più o meno faticoso.
Mi sono ispirato a un disegno di Bruno Ernst.
9 settembre
2019
Comincia la scuola!
A tutti i colleghi insegnanti,
agli studenti e ai genitori
auguro un anno scolastico pieno di successi!
Nelle vostre programmazioni prevedete di far ridere di cuore gli alunni almeno una volta ogni lezione!
Per chi ama la matematica, propongo un gioco: trovate il cuore segreto della matematica nella seguente figura.
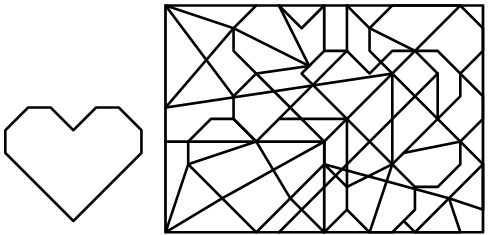
Avete visto un cuore?
Ok, adesso trovate l'altro, quello segreto. Ci sono due cuori uguali... pardon, congruenti.
7 settembre
2019
33 è la somma di tre cubi di numeri interi [aggiornato]
Dal Forum di BASE Cinque, siamo lieti di comunicarvi nientepopodimenoché:
42=(−80538738812075974)3+804357581458175153+126021232973356313
Qui si può leggere qualcosa di interessante su questa e altre simili rappresentazioni 'resistenti'.
25 agosto 2019
The Hermetically Open Archive
THE RITMAN LIBRARY è una biblioteca privata in Amsterdam che ospita circa 25000 libri e manoscritti ermetici.
La biblioteca ha iniziato a scansionare e pubblicare online una selezione di 5.000 libri e 300 manoscritti in un archivio chiamato The Hermetically Open Archive.
In questo archivio ho trovato un libro piuttosto singolare:
Thomas Taylor, The elements of the true arithmetic of infinities, London, 1809.
Ecco alcune proposizioni che mi hanno incuriosito.
Che sia un precursore dell'analisi non standard?
20 agosto 2019
L'operazione di Kaprekar [continua]
Parliamo dell'operazione di Kaprekar.
Questo procedimento è un algoritmo conosciuto come operazione di Kaprekar o routine di Kaprekar.
Va bene, ma ora ci sono tre domande:
15 agosto 2019
L'operazione di Kaprekar
Prendi il numero 6174.
L'hai preso?
Scrivi le sue cifre in ordine decrescente. Che numero ottieni?
7641.
Scrivi le sue cifre in ordine crescente. Che numero ottieni?
1467.
Calcola la differenza tra i due numeri. Che numero ottieni?
7641-1467 = 6174.
Ma dai?!
E' il numero di partenza!
Ripeti la procedura con qualunque altro numero di 4 cifre NON tutte uguali.
Cosa succede?
Non funziona come prima?
Insisti.
Arriverai sempre a 6174.
Alcuni chiamano questo numero costante di Kaprekar.
Dattatraya Ramchandra Kaprekar (1905-1986)
10 agosto 2019
Umorismo matematico 2019 [aggiornato]
Newton alla festa della birra
Takebe Katahiro (1664-1739) è ritenuto il fondatore del calcolo infinitesimale in Giappone.
5 agosto 2019
Umorismo matematico 2019 [aggiornato]
Pensiero improvviso
Gauss (1777-1855) pensa che i numeri immaginari introdotti da Gerolamo Cardano (1501-1576) forse esistono davvero.
31 luglio 2019
Umorismo matematico 2019 [aggiornato]
Cartesio su Facebook
Nota per i posteri: il modo stravagante di scrivere certi problemini sui social e soprattutto affermare che chi li risolve è un genio, potrebbe scatenare reazioni allergiche nei matematici. Ma è meglio sorridere, dài.
25 giugno 2019
Il paradosso sociale del PEMDAS
Cari amici, stenterete a crederci, ma è da circa 8 anni (2011-2019) che nei social e in vari forum si discute di questa espressione aritmetica:
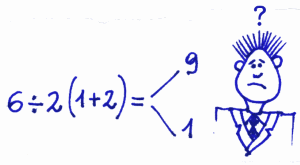
Qual è il suo valore: 9 oppure 1?
O c'è dell'altro?
Vedremo...
21 giugno 2019
Cari amici, auguro a tutti voi felici vacanze
dovunque voi siate, ai monti, al mare, in campagna, in città!
credit: Mohammed Hassan, (https://freeimagesandillustrations.blogspot.com)
18 giugno 2019
Umorismo matematico 2019 [aggiornato]
Io e Gödel
16 giugno 2019
Il paradosso toroidale di Herbert Taylor
Un vecchio problema finalmente risolto su BASE Cinque.
La figura rappresenta due forme intrecciate.
Immaginatele come due palloncini di gomma infinitamente elastica. Considerate solo la loro superficie.
Per la precisione sono superfici di tori, uno di genere 1 (un buco) e l'altro di genere 2 (due buchi).
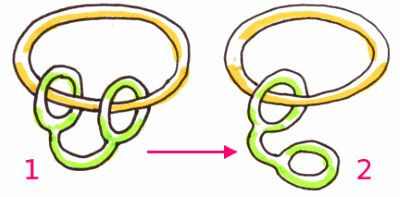
Come si fa per trasformarle l'una nell'altra con una deformazione continua, senza fare né tagli né saldature?
Disegnate le varie fasi.
14 giugno 2019
Fare pace con la topologia [aggiornamento]
Carta, matita, gomma, penna, evidenziatore verde.
E' davvero rilassante disegnare trasformazioni topologiche!
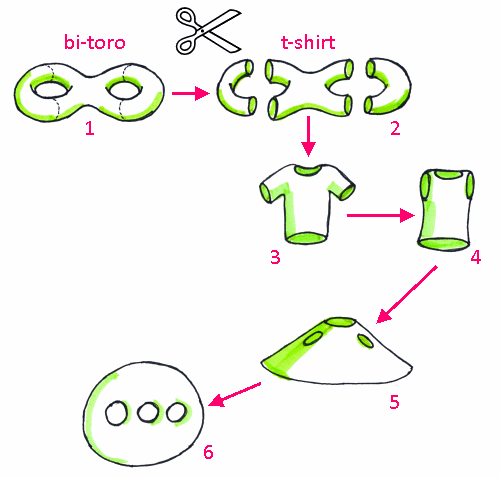
La t-shirt, considerata come una superficie, ha 2 dimensioni anche se è immersa nello spazio a 3 dimensioni. La figura mostra che è topologicamente equivalente alla parte centrale di un bi-toro tagliato e a un cerchio con tre buchi.
5 giugno 2019
Il pretzel o brezel è un tipo di pane formato da un cordoncino di pasta intrecciato come si vede nella figura qui sotto.
E' anche il nome della forma geometrica n. 3, formata da due anelli incatenati collegati fra loro con un cilindro.
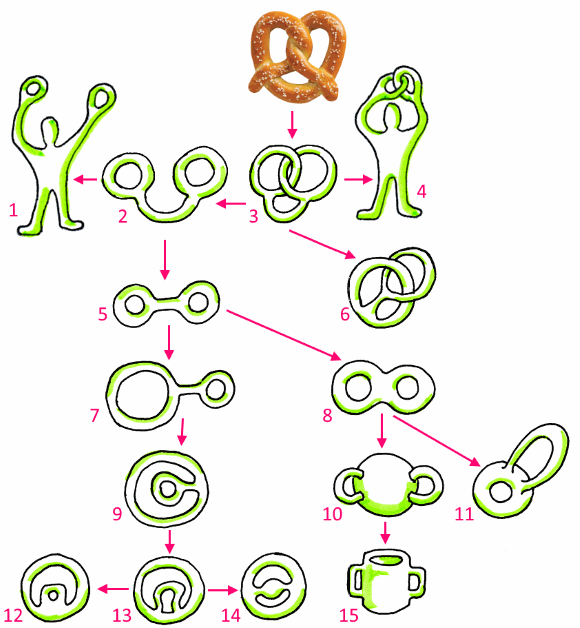
Le forme 2 e 3 sono topologicamente equivalenti, ma come si fa a trasformarle l'una nell'altra con una deformazione continua, senza tagliare un anello?
30 maggio 2019
Fare pace con la topologia [aggiornamento]
Aggiornato, con la motivata risposta alla domanda fondamentale: quanti buchi ha una t-shirt?
28 maggio 2019
Punti di vista - Elezioni Europee 2019 - Italia
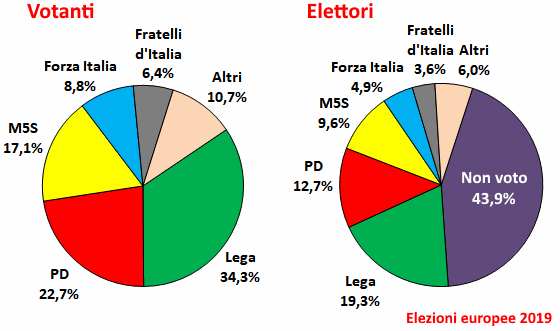
Grafici aggiornati ai risultati definitivi, fonte "la Repubblica", 28 maggio 2019.
Non ho i dati sulle schede bianche e/o nulle. Nel 1994 corrisposero al 5% dei votanti e al 3% degli elettori.
27 maggio 2019
Cari amici, ultimamente al Forum di B5 si parla di Martin Gardner.
Sono andato a pescare un frammento di pagina ingiallita della rivista LE SCIENZE, edizione italiana di Scientific American del 1973, n.53.
Il titolo della mitica rubrica tenuta da Martin Gardner.
Ho scelto 10+ problemini facilissimi e ve li propongo, in ordine sparso.
25 maggio 2019
La topologia è una materia affascinante ma dura. E' difficile passare da pensieri intuitivi e apparentemente semplici alla loro rappresentazione matematica.
Per me è stata la materia più difficile all'università, troppi anni fa.
Per esempio, qual è la soluzione di questo problemino ricreativo?
---
Quanti buchi ha questa maglietta (t-shirt)?
---
A un certo punto, ho deciso di fare pace con la topologia.
Non chiedo molto: niente assiomi, teoremi, formule, mi basta rendere più precise le intuizioni elementari.
Ed ecco che viene in soccorso un illuminante articolo del grande matematico Gino Fano (1871-1952). Meravigliosa lettura che consiglio a tutti.
La citazione precisa è:
Gino Fano, L'analysis situs I. Scientia, Vol. 36 (1924), p. 217–230.
Si può consultare online qui: https://amshistorica.unibo.it/7.
L'articolo è disponibile anche su BASE Cinque in formato PDF.
Gino Fano, L'analysis situs I. Scientia, Vol. 36 (1924), p. 217–230 (PDF)
10 maggio 2019
Umorismo matematico 2019 [aggiornato]
Interessanti le vignette di Tom Gauld su Twitter.
Ecco un esempio matematico-scientifico tradotto in italiano.
Credit: Tom Gauld, Twitter.
3 maggio 2019
33 è la somma di tre cubi di numeri interi [aggiornato]
Cari amici, potreste dire: OK, e a me che me ne frega? Who cares?
Dài, se siete qui vuol dire che un po' ve ne frega.
E' facile trovare tre interi i cui cubi diano come somma 29 o 34.
Per esempio:
29 = 13+13+33 = 1+1+27
34 = (-1)3+23+33 = -1+8+27
34 = 53+(-4)3+(-3)3 = 125-64-27
Ma che dire di 32 e 33?
Per il 32, la dimostrazione è abbastanza facile.
Invece, trovare tre cubi la cui somma sia 33 è molto più difficile, tant'è vero che la questione è stata risolta solo nel 2019 da Andrew Booker.
Vedi: Cracking the problem with 33 di Andrew Booker, University of Bristol, UK.
Nessuno sa ancora se esistono tre cubi di numeri interi la cui somma è 42.
x3+y3+z3 = 42
Questa è una sfida.
23 aprile 2019
Carte sopra, carte sotto, di Nobuyuki Yoshigahara
Ecco un esempio di originalità.
Se volete inventare un gioco con le carte per origami, forse la prima cosa che vi viene in mente è di piegarle in qualche modo.
Nobuyuki Yoshigahara (1936-2004), per gli amici Nob, ha invece creato un gioco completamente diverso: un labirinto multistato.
Eccolo.
Nella figura vedete molte carte da origami sparse su un tavolo.
Ogni carta può essere sopra oppure sotto un'altra carta.
Partite dalla carta con scritto "INIZIO" e trovate un percorso fino alla carta con scritto "FINE". Anzi: trovate il percorso più breve.
Dovete spostarvi da una carta a quella successiva andando alternativamente: sali, scendi, sali, scendi, ...
Stampate questo labirinto e provate a risolverlo.
Se non volete stamparlo, potete scaricare l'immagine e lavorarci con un semplice programma di disegno, tipo "paint" per Windows.
Beh, per saperne di più leggete l'articolo.
18 aprile 2019
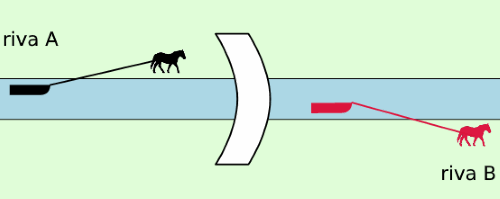
Che percorso deve seguire il cavallo per passare dalla riva A alla riva B attraversando il ponte?
Per questo problema mi sono ispirato al MathsJam Annual Gathering 2018, vedi per esempio: Big MathsJam Highlights, 2018, di Colin Beveridge, su The Aperiodical.
16 aprile 2019
Ricordo di Grazia Raffa
Cari amici vecchi e nuovi di BASE Cinque, desidero ricordare qui la poetessa Grazia Raffa e inviarle al cielo un ringraziamento per averci mostrato il lato poetico della matematica.
Grazia Raffa (1931-2018)
Ecco alcune sue poesie ispirate a temi e protagonisti della matematica.
Un particolare ringraziamento va a Ivana Niccolai che ha bussato alle porte della nostra memoria segnalandoci la biografia della poetessa pubblicata sul sito di Maecla: http://www.maecla.it/GraziaRaffa/index.htm.
Credit foto: Giorgio Pietrocola
14 aprile 2019
I labirinti logici di Robert Abbott
Entra nel labirinto e trova l'uscita. Però...
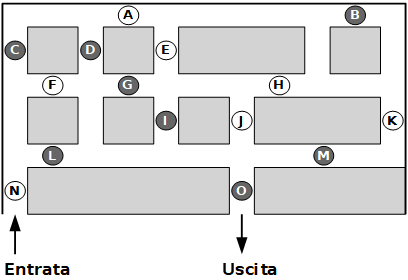
Nel labirinto sono disegnati per terra dei dischi neri e dei dischi bianchi. Nel tuo percorso devi attraversare alternativamente un disco bianco, uno nero, uno bianco uno nero, e così via fino all'uscita.
Le lettere scritte nei dischi servono per descrivere la tua soluzione con una sequenza di lettere.
Non è necessario attraversare tutti i dischi.
Regole.
a) Una volta entrati in un disco, bisogna attraversarlo completamente, ovvero non è ammesso fare dietro-front quando ci si trova su un disco.
b) Si può passare più volte sullo stesso disco (ma non successive perché
in tal caso non ci sarebbe il cambio di colore).
31 marzo 2019
Il giorno dopo l'arrivo di Jinping c'ero anch'io a Roma, per altri motivi.
Stazione di Roma Termini. Davanti a me un'ora di attesa (di cui 50% per ritardo treno) e 5 ore di viaggio.
Quasi quasi mi compro un libro.
Ecco la mia recensione.
29 marzo 2019
Questa mi è piaciuta.
Si trova in molti siti, tra cui: https://www.facebook.com/Ingegneriaedintorni
15 marzo 2019
Sulla storia della matematica ricreativa a Lisbona
A partire dal 2009, ogni 2 anni, l'associazione portoghese Ludus organizza, assieme ad altri enti, un colloquium di matematica ricreativa (seminario accademico).
Il 29 gennaio si è concluso a Lisbona il sesto colloquium.
Ecco tre link utili:
Da parte mia ho fatto qualche indagine sull'intervento di Tereza Bártlová, History of recreational mathematics.
Wow, la sua tesi di dottorato è disponibile on-line e si può scaricare in formato PDF qui: https://is.cuni.cz/webapps/zzp/download/140052164
Tereza Bartlova, History and current state of recreational mathematics and its relation to serious mathematics, Charles University in Prague, 2016.
E' bello avere una continuazione dell'opera del mitico David Singmaster che, tra l'altro, era attivamente presente al colloquium.
1 marzo 2019
Aritmetica mentale nella scuola di Rachinski (3)
Alcuni esercizi tratti dal libro 1001 sfide di calcolo mentale, di Sergey Aleksandrovich Rachinsky, ristampato nel 2017.
I testi degli esercizi in russo si possono scaricare da questa pagina, il link si trova verso il fondo dell'articolo:
(http://baby-ved.ru/kopilka/sergey-aleksandrovich-rachinsky/).
28 febbraio
2019
Aritmetica mentale nella scuola di Rachinski (2)
Per questa seconda puntata, ho ripreso un vecchio articolo già presente nel sito.
Come si può risolvere questa espressione usando soltanto il calcolo mentale?
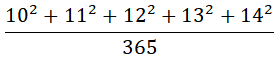
27 febbraio
2019
Aritmetica mentale nella scuola di Rachinski (1)
Cari amici, abbiamo già parlato del quadro che vedete qui sotto.
Nicolai Petrovich Bogdanov Belski
(1868-1945)
Aritmetica mentale nella scuola di Rachinski (1895)
-
Finalmente sono riuscito a scaricare il libro 1001 sfide di calcolo mentale, di Sergey Aleksandrovich Rachinsky, ristampato nel 2017
(http://baby-ved.ru/kopilka/sergey-aleksandrovich-rachinsky/).
Peccato che è scritto in russo!
Tuttavia, grazie al traduttore di Google, ho chiarito alcuni aspetti per me misteriosi.
Condivido con voi questi appunti, in tre puntate: la prima è dedicata al dipinto, la seconda al problema scritto alla lavagna e la terza al libro.
Chiunque desideri dare un contributo è benvenuto/a!
18 febbraio
2019
Umorismo matematico 2019 [aggiornamento]
Il paradosso del generatore di fake news.
Ieri ho letto questa notizia.
OpenAI mette a punto generatore automatico di fake news (false notizie). Ma decide di tenere segreto l'algoritmo per paura di sconvolgimenti mondiali.
L'algoritmo, chiamato GPT2, è un generatore di testi che è stato addestrato con circa 10 milioni di articoli, scelti tra quelli i cui link avevano più di tre voti sulla piattaforma Reddit, una quantità 15 volte maggiore rispetto a quella usata normalmente per le AI di questo tipo.
Il risultato è che, dato un qualunque incipit, l'algoritmo riesce a proseguire scrivendo testi plausibili e senza gli errori che fanno normalmente le macchine.
Nota. OpenAI è un'organizzazione non profit di ricerca sull'intelligenza artificiale, fondata nel 2015 da Elon Musk e Sam Altman.
---
In un esperimento, i ricercatori hanno chiesto a GPT2 di scrivere una notizia a proposito di se stesso.
Ebbene, l'algoritmo ha confermato di essere un generatore di fake news potenzialmente pericoloso.
OK, ora mi viene un dubbio...
11 febbraio
2019
Ho aggiornato la pagina dei Quattro quattro dove ho trovato un problemino ancora aperto.
Thomas Rayner Dawson, nel 1916, fu (forse) il primo a porre il problema dei quattro quattro in termini più generali.
E' possibile, utilizzando quattro R e le operazioni/funzioni aritmetiche, esprimere i numeri interi da 0 a 10?
R indica un numero intero positivo.
Sono ammesse le quattro operazioni, i radicali, l'elevamento a potenza, il fattoriale, il punto decimale.
Per esempio:
0 = R + R - R - R
1 = R ∶ R + R - R
2 = R ∶ R + R ∶ R
3 = (R + R + R) ∶ R
Ho postato il problema anche al Forum, se avete una soluzione, condividetela!
7 febbraio
2019
Cari amici, l'ultima volta che ho dedicato una pagina al Lato comico è stato nel 2013.
I tempi sono cambiati, ed è venuto il momento di creare una nuova pagina sull'umorismo matematico.
4 febbraio
2019
Tre problemi da un libro di 40 anni fa...
Cari amici, oggi vorrei ricordare il libro di D. O. Shklyarskij, N. N. Chentsov, I. M. Yaglom, Selected problems and Theorems in Elementary Mathematics. Arithmetic and Algebra, MIR Publishers, Moscow, 1976, 1979.
Ecco tre problemi tradotti liberamente. A prima vista sembrano difficili, ma non lo sono.
Problema 47. Dimostra che per ogni intero n
a) n7 - n è divisibile per 7
b) n9 - n NON SEMPRE è divisibile per 9
c) n11 - n è divisibile per 11
Problema 64. Dimostra che ogni numero naturale formato da 3n cifre uguali è divisibile per 3n. (per esempio 222 è divisibile per 3, 777.777.777 è divisibile per 9 e così via).
Problema 107. Su una lavagna sono scritti tutti i numeri interi da 1 a 1.000.000.000 (estremi compresi).
Un folletto sostituisce ogni numero con la somma delle sue cifre.
Per esempio, cancella il numero 8637 e al suo posto scrive 24. I numeri da una
cifra rimangono invariati.
Poi sostituisce di nuovo ogni risultato con la somma delle sue cifre e ripete l'operazione fino a quando sulla lavagna sono scritti soltanto numeri da una cifra.
A questo punto, sulla lavagna c'è scritto più volte il numero 1 o il numero 2?
29 gennaio
2019
Visitare tutte le celle di una griglia
Dove finisce il gioco e dove comincia la matematica "seria"?
Anche quest'anno ho tenuto un piccolo laboratorio di matematica ricreativa allo stage del DIMA di Genova.
Lo stage (di 4 giorni) è rivolto agli studenti degli ultimi anni delle scuole superiori indecisi sulla scelta universitaria e che stanno valutando la possibilità di iscriversi al corso di studi in Statistica o in Matematica (vedi: Stages al DIMA).
Mi è davvero piaciuto come gli studenti (15) del mio gruppo hanno affrontato e risolto un problema che gli ho proposto. Hanno lavorato bene anche con gli altri problemi, ma questo ha avuto una marcia in più.
Ho già accennato a questo problema alcuni giorni fa. Qui cercherò di riportare le fasi principali della sua risoluzione come è stata costruita dagli studenti.
Ecco il problema, posto soltanto con un disegno, senza parole.
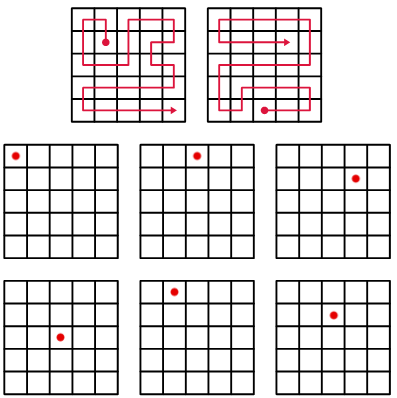
Questo tipo di problema appartiene alla matematica ricreativa da almeno 100 anni ma la fonte principale che mi ha spinto a riprenderlo è l'articolo di James Tanton, Personal stories of discovering mathematics, su Medium, 2018.
23 gennaio
2019
Lascio un memo: Google+, la rete sociale di Google, chiuderà i servizi gratuiti ad aprile 2019. Peccato.
Ora c'è la fase della migrazione di massa. Spuntano molte alternative e vorrei segnalarne una di qualità per i matematici: StackExchange.
StackExchange è una rete nata nel 2008 in cui si possono porre domande su vari argomenti. Ci sono almeno cinque sezioni e sottosezioni che riguardano la matematica.
Recreational Mathematics (tag)
Elementary Number Theory (tag)
15 gennaio
2019
Cari amici, Math without words (Matematica senza parole) di James Tanton è una collezione di 75 problemi profondamente matematici e nello stesso tempo accessibili a tutte le persone della Terra.
Non importa che lingua parli. Se ti piace la matematica, li capirai al volo, perché non c'è scritta neppure una parola. Sono pura matematica.
Il libro è in vendita ma James Tanton ha lasciato (volutamente) qualche traccia nella rete, dalla quale traggo due esempi, per darvi l'idea.
James Tanton è su Twitter https://twitter.com/jamestanton.
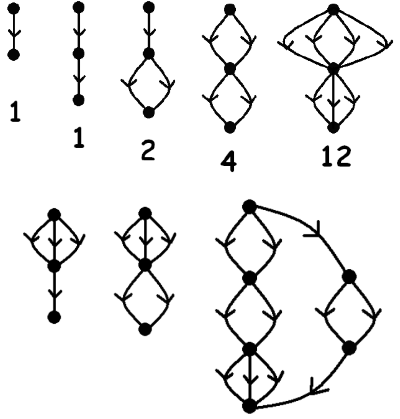
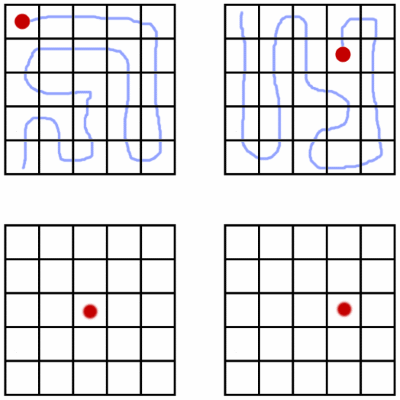
James Tanton, Math without words, 2008
11 gennaio
2019
Cari amici, ho aggiunto alla galleria degli esperimenti visionari lo stencil di un noto personaggio della politica italiana.
Sedetevi comodamente a un tavolo perché l'esercizio richiede calma e concentrazione.
Potete guardare la figura direttamente sullo schermo oppure stampata su un foglio di carta. La figura deve essere ben ferma.
Fissate per circa 15 secondi la crocetta che si trova al centro del naso. Non muovete gli occhi.
Poi guardate la parete bianca di fronte a voi.
Cosa vedete?
Dovreste vedere un cerchio chiaro.
Battete due o tre volte le palpebre e guardate meglio dentro al cerchio.
Cosa vedete?
Altre immagini si trovano nella pagina: Un signore con la barba.
Nella pagina Jesus! è spiegato come creare queste figure, anche a colori.
Ho pubblicato questo esercizio esclusivamente a scopo scientifico.
Ma non chiedo finanziamenti pubblici.
8 gennaio 2019
Cari amici, abbiamo visto che un numero semprimo è il prodotto di due soli numeri primi, per esempio 26 è semiprimo perché:
26 = 2 × 13
Cos'è un numero felice (happy number)?
Facciamo la somma dei quadrati delle sue cifre.
Ripetiamo l'operazione con il numero che abbiamo ottenuto.
Se, ripetendo questa operazione, arriviamo a ottenere 1 allora il numero è felice.
Per esempio, 2019 è felice perché:
22 + 02 + 12 + 92 = 86
82 + 62 = 100
12 + 02 + 02 = 1
Invece 20 non è felice perché dà luogo a una sucessione che si ripete illimitatamente.
[20-4-16-37-58-89-145-42]-20-...
La sequenza è formata da 8 numeri perciò ha periodo 8.
I numeri non-felici danno luogo sempre a sequenze di periodo 8? Da indagare.
Per fare indagini, c'è un programmino javascript in La pagina aperta del 153.
Qual è la definizione di numero fortunato (lucky number)?
La cosa è un po' più difficile delle due precedenti.
In pratica non c'è una formula per scoprire subito se un numero è fortunato. Bisogna invece costruire la sequenza dei numeri fortunati.
Partiamo dalla sequenza dei numeri interi positivi.
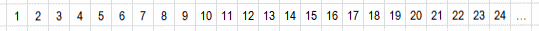
Il numero 1 è fortunato per definizione, lasciamolo stare.
Il primo numero dopo l'1 è il 2 perciò cancelliamo ogni secondo numero della sequenza (si contano due posizioni, si elimina il secondo e si riparte col conteggio e così via).
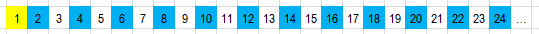
Rimane la lista dei numeri dispari.
Il primo numero rimasto dopo l'1 è 3. Cancelliamo ogni terzo numero della lista rimasta (si contano tre posizioni, si elimina il terzo e si riparte col conteggio e così via).
Il primo numero rimasto dopo il 3 è 7. Cancelliamo ogni settimo numero della lista rimasta.
Il primo numero rimasto dopo il 7 è 9. Cancelliamo ogni nono numero della lista rimasta.
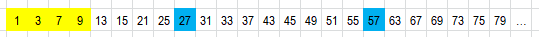
... e così ì via, illimitatamente...
1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, ...
I numeri che sopravvivono a questa cancellazione di massa illimitata sono quelli fortunati!
Gli altri sono sfortunati.
Questo procedimento assomiglia al crivello di Eratostene ma genera un insieme di numeri diverso da quello dei numeri primi.
1 gennaio 2019
Cari amici, ho consultato l'OEIS a proposito del 2019 e vi comunico con piacere che:
perciò possiamo stare tranquilli: il 2019 sarà un anno felice e forunato per tutti!
Ecco altre due curiosità.
E' un numero semprimo cioè è il prodotto di due soli numeri primi (https://oeis.org/A001358):
2019 = 3 × 673
E' un numero composto tale che ogni concatenazione dei suoi fattori primi è un numero primo (https://oeis.org/A217263)
3673 è primo, 6733 è primo.
BASE Cinque augura un prospero 2019 all'OEIS, inesauribile miniera di preziose informazioni per i matematici di tutto il mondo.
The On-Line Encyclopedia of Integer Sequences® (OEIS®)
.
.
.
Pace e bene a tutti!
Gianfranco Bo
Data creazione: dicembre 2019
Ultimo aggiornamento: dicembre 2019
xhtml 1.1
Sito Web realizzato da Gianfranco Bo